Исследовательская работа по теме "Циклоиды"

Исследовательская работа

по геометрии

«циклоиды»

Выполнил: студент группы кск-20нп

Агапитов В.В

• Познакомиться с основным свойствами циклоида и ее проявлениями в жизни

• Изучить методическую литературу по теме исследования
• Пополнить знания о разновидностях циклоиды и их свойствах
• Узнать о значении и применении циклоиды в жизни, окружающем мире и быту

Приложим к нижнему краю классной доски линейку

и будем катить по ней обруч или круг, прижимая его к линейке

и к доске. Если прикрепить к обручу или кругу кусок мела

(в точке соприкосновения его с линейкой), то мел будет вычерчивать кривую, называемую циклоидой.

Определяется она как кривая, которую описывает точка обода колеса, катящегося без проскальзывания по прямой линии.

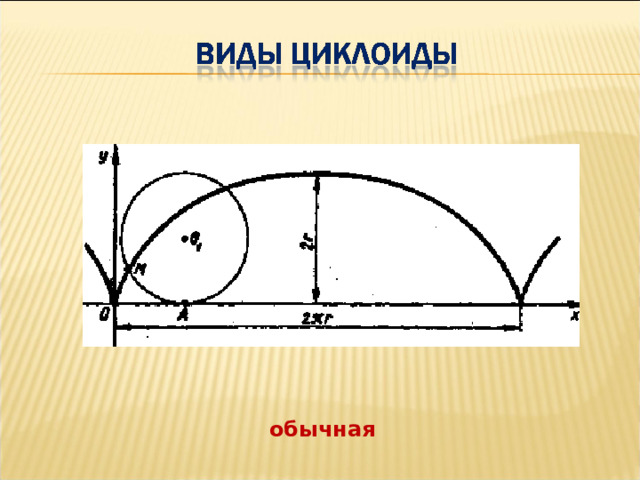
обычная

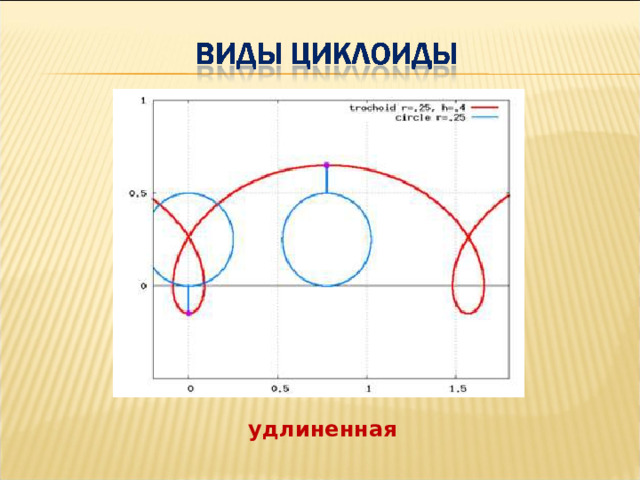
удлиненная

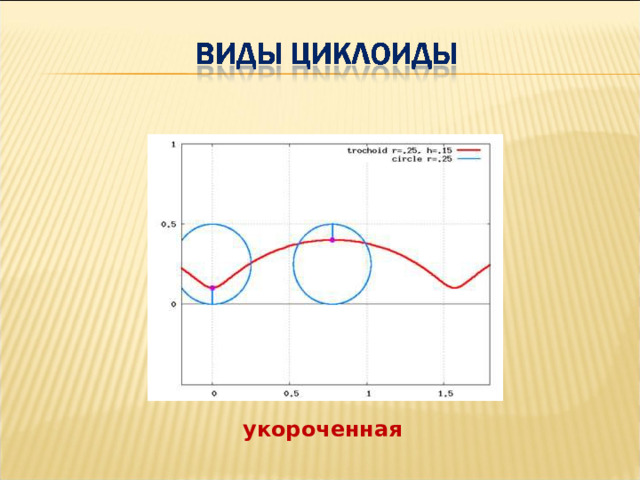
укороченная

Древние ученые не знали циклоиду, но они знали и успешно пользовались ее близкой родственницей – эпициклоидой.

Если радиус

неподвижной окружности

равен радиусу подвижной,

то эпициклоиду называют

кардиоидой (по-гречески

означает«сердцевидная»).

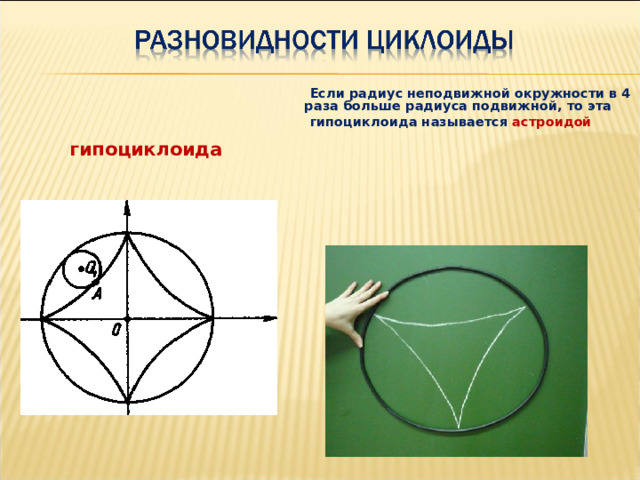
Если радиус неподвижной окружности в 4 раза больше радиуса подвижной, то эта

гипоциклоида называется астроидой

гипоциклоида

Первым, кто стал

изучать циклоиду,

был Галилео

Галилей. Он же и

придумал название

«циклоида»

(«напоминающая о

круге»)

1. Циклоида – периодическая кривая.

Касательная прямая — прямая, проходящая

через точку кривой и совпадающая с ней в

этой точке.

Нормаль — это прямая, перпендикулярная

касательной прямой к некоторой кривой.

Обратим внимание на положение касательной к циклоиде.

Если велосипедист едет по мокрой дороге,

то оторвавшиеся от колеса капли будут лететь по касательной к циклоиде

и при отсутствии

щитков могут

забрызгивать

спину велосипедиста.

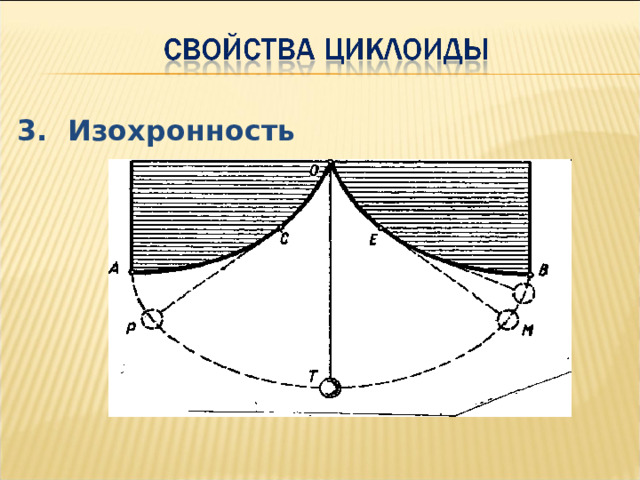
3. Изохронность

4. Брахистохронное свойство

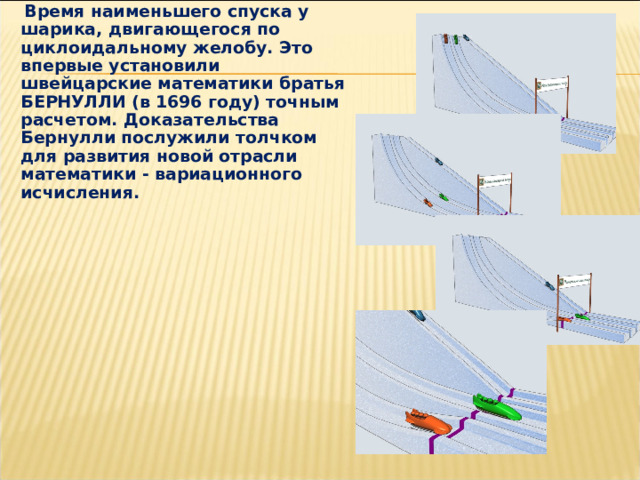
Время наименьшего спуска у шарика, двигающегося по циклоидальному желобу. Это впервые установили швейцарские математики братья БЕРНУЛЛИ (в 1696 году) точным расчетом. Доказательства Бернулли послужили толчком для развития новой отрасли математики - вариационного исчисления.

Если мы заставим первую монету катиться по второй так, чтобы она прошла ровно половину окружности (как указано стрелкой), мы можем ожидать, что, придя к точке, диаметрально противоположной первоначальной, монета перевернется вниз головой по сравнению с исходной позицией. Мы убеждены, что, пройдя половину окружности, монета должна повернуться на 180°. Если же мы проделаем эксперимент с реальной монетой, то убедимся, что она окажется снова в исходном положении — будто бы она прошла полную окружность, а не ее половину.

Если мы заставим первую монету катиться по второй так, чтобы она прошла ровно половину окружности (как указано стрелкой), мы можем ожидать, что, придя к точке, диаметрально противоположной первоначальной, монета перевернется вниз головой по сравнению с исходной позицией. Мы убеждены, что, пройдя половину окружности, монета должна повернуться на 180°. Если же мы проделаем эксперимент с реальной монетой, то убедимся, что она окажется снова в исходном положении — будто бы она прошла полную окружность, а не ее половину.