Презентация научно-исследовательского проекта на тему "Циклоида"

Научно-исследовательская работа ученицы АОУ гимназии №9 5 «В» класса Варзиной Ирины. Научный руководитель: Чайка Г.К.

Изучить циклоиду и ее свойства.

• Изучить и проанализировать литературу, собрать данные о циклоиде.
• Дать определение циклоиды и показать способы ее построения.
• Изучить биографии ученых, которые занимались

циклоидой.

- Изучить свойства, которыми обладает циклоида.

• Провести эксперименты, демонстрирующие

свойства циклоиды, имеющие практическое применение.

- Сделать выводы.

Блез Паскаль :

«Циклоида является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии.»

Кривая, которая получается как траектория движения точки , закрепленной на окружности, катящейся без скольжения по прямой, называется циклоидой.

Галилео Галилей (1564 – 1642)

Циклоида –

самая популярная кривая 17 века!

Гюйгенс

Декарт

Лейбниц

Ньютон

Арка циклоиды

(брахисто - кратчайший + хроно – время )

Кривая наискорейшего спуска

прямая

окружность

циклоида

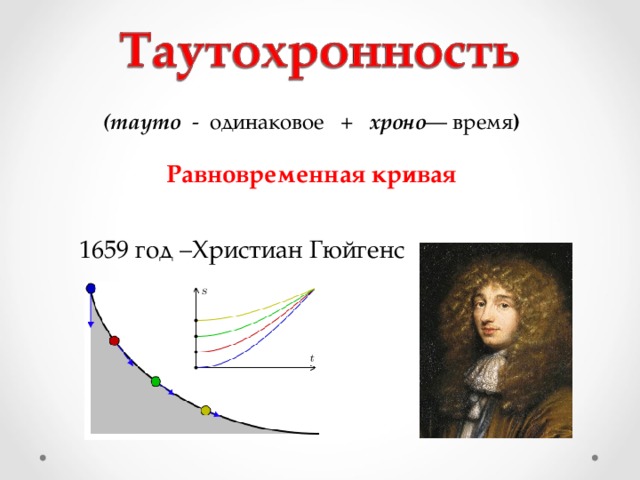
(тауто - одинаковое + хроно — время )

Равновременная кривая

1659 год –Христиан Гюйгенс

циклоиды

Построение

циклоиды

Проверка

свойств:

брахистохронность

и

таутохронность

Модель

таутохронного маятника

Длина арки циклоиды 8r.

r

4r

• Циклоида действительно замечательная кривая.
• Я выяснила, что сейчас циклоида имеет огромное практическое применение.
• Циклоида неразрывно связана с одним из самых интересных периодов в истории математики, когда знаменитые математики изобрели приемы, без которых не может обойтись современная математика, физика, промышленность.

Иоганн Бернулли :

“ Я должен еще раз выразить восхищение, которое я чувствую по поводу неожиданного тождества таутохроны Гюйгенса и моей брахистохроны».

Аристотель. «Мы с наслаждением познаём математику… Она восхищает нас, как цветок лотоса».

Спираль Архимеда

Улитка Паскаля

Кривая Коха

Циклоида – брахистохрона

Циклоида – таутохрона