Министерство образования Республики Башкортостан
Отдел образования администрации МР Илишевский район
Муниципальное бюджетное общеобразовательное учреждение
средняя образовательная школа №4
с. Верхнеяркеево
Исследовательская работа
Системы счисления и их применение
Автор: Аглямова Алия,
учащаяся 10 класса
Руководитель: Аглямова Г.М.,
учитель информатики
с. Верхнеяркеево
2017
Содержание
Введение...............................................................................3
1. Подготовка к исследованию……..…….….....……….............5
1.1 Исторические сведения..........................................5
1.2 Сбор информации ..................................................6
1.2.1 Египетская система счисления.......................7
1.2.2 Африка каменного века....................................8
1.2.3 История римской системы счисления........….9
1.2.4 Система счисления Древней Руси............…...….9
1.2.5 Различия системы счисления.........………..…..….10
1.2.6 Машинная группа систем счисления......….….11
1.3 Проведение анкетирования...................................14
2. Проведение исследования............................................15
2.1 Первый этап исследования....................................15
2.2 Второй этап исследования.....................................18
2.3 Заключительный этап исследования…………...22
Заключение.............................................................................23
Список литературы...............................................................24
Введение
Числа сопровождают нашу жизнь повсюду. В самые древние времена люди считали на пальцах, т. е. понятие число, в котором мы привыкли его понимать, у них не было.
Память человечества не сохранила, не донесла до нас имя изобретателя колеса или гончарного круга. Это и неудивительно: более 10 тысяч лет прошло с тех пор, как люди всерьез занялись земледелием, скотоводством и производством простейших товаров. Назвать же имя гения, впервые задавшего вопрос «Сколько?», тем более невозможно.
Способов счета было придумано немало: люди рисовали палочки на стенах и делали зарубки на костях животных или ветках деревьев. Такая система записи чисел называется единичной. Любое число в ней образуется повторением одного знака - единицы. Для записи больших чисел используются группировки и вспомогательные значки.
Поштучно считать предметы удобно тогда, когда их не очень много, т. к. чем большее число надо записать, тем длиннее будет строка из палочек.
Поэтому нам интересно знать, как появились числа, как их записывали и какими цифрами пользуемся мы сейчас.
Сейчас в большинстве стран мира, несмотря на то, что там говорят на разных языках, считают одинаково, "по-арабски". Но так было не всегда. Еще каких-то пятьсот лет назад ничего подобного и в помине не было даже в просвещенной Европе, не говоря уже о какой-нибудь Африке или Америке.
Данная тема была выбрана, потому что стало интересно узнать, кто стоит у истоков различных систем счисления, как давно и где их начали применять, почему двоичная система счисления сохранилась до наших дней.
Была поставлена следующая цель: изучить роль двоичной системы счисления и познакомиться с иными системами счисления.
Для достижения поставленной цели сформулировали следующие задачи:
изучить литературу о различных системах счисления,
провести анкетирование учащихся
подробнее рассмотреть двоичную систему счисления,
узнать чем удобна двоичная система счисления и где она используется.
Описание объекта и предмета исследования
Объект исследования: системы счисления .
Система счисления - это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.
Предмет исследования: исследование темы «Системы счисления и их применение»
Методы исследования:
1. теоретический: теоретический анализ литературных источников;
2. эмпирический: сравнение, социологический опрос-анкетирование.
Теоретическая значимость моего исследования заключается в том, что многие подростки и не только, возможно обратят внимание на моё исследование, и сделают выводы, подтверждая их действиями.
Практическая значимость исследования состоит в том, что оно может быть использовано школьниками для повышения образовательного уровня, учителем математики и информатики для объяснения тем и проведения занимательных уроков.
1. Подготовка к исследованию
1.1. Исторические сведения
В начале, немного из истории возникновения чисел:
В каменном веке, когда люди собирали плоды, ловили рыбу и охотились на животных, потребность в счете возникла так же естественно, как и потребность в добывании огня. Об этом свидетельствуют находки археологов на стоянках первобытных людей. Например, в 1937 году в Вестонице (Моравия) на месте одной из таких стоянок найдена волчья кость с 55 глубокими зарубками. Позже в других местах ученые находили столь же древние каменные предметы с точками и черточками, сгруппированными по три или по пять.
Развитие чисел тесно связано с потребностями общества в измерениях, контроле, особенно в областях аграрной, промышленной и налогообложения. Первые области применения чисел были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов. Понятие числа всегда сопровождалось и нечисловыми понятиями. Например, один, два, много. Эти нечисловые понятия всегда ограждали числа. Числа придавали законченный вид всем наукам, где они применялись.
Язык чисел, как и обычный язык, имеет свой алфавит. В том языке чисел, которым сейчас пользуются практически на всём земном шаре, алфавитом служат десять цифр от 0 до 9. Этот язык называется десятичной системой счисления. Однако не во все времена и не везде люди пользовались десятичной системой счисления. С точки зрения чисто математической она не имеет специальных преимуществ перед другими возможными системами счисления, и своим повсеместным распространением эта система обязана вовсе не общим законам математики, а причинам совсем иного характера. О свойствах, истории возникновения и применения различных систем счисления будет рассказано в нашей работе.
Потребность в записи числа появилась в очень древние времена, как только люди начали считать.
Представим себе то далекое время, когда люди только начали изобретать числа. В те времена для счета человеку хватало четырех слов: один, два три и много. Именно так считают и сейчас некоторые племена, живущие в джунглях Южной Америки. С развитием человечества этих слов стало не хватать. Земледельцу надо было подсчитать урожай, скотоводу животных, строителю количество бревен Умение считать и производить операции с числами высоко ценилось. Числа вызывали удивление, потому что они могли обозначать количество любых предметов, например, два пальца, две руки, два человека или два камня.
Поэтому появился счет группами, так появились первые нумерации - системы счисления.
Со времени их происхождение сформировалось большое количество отличных систем счисления: пятеричная, десятичная, мультипликативная
1.2. Сбор информации
Ученые считают, что история возникновения чисел зародилась еще в доисторические времена, когда человек научился считать предметы. Но знаки для обозначения чисел появились значительно позже: их изобрели шумеры — народ, живший в 3000—2000 гг. до н. э. в Месопотамии (ныне в Ираке). История гласит, что на табличках из глины они выдавливали клинообразные черточки. Вавилоняне, пришедшие в Месопотамию после шумеров, унаследовали многие достижения шумерской цивилизации — сохранились клинописные таблички с переводом одних единиц измерения в другие.
1.2.1. Египетская система счисления
Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э.), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах. Из этих надписей нам известно, что древние египтяне использовали только десятичную систему счисления. Единицу обозначали одной вертикальной чертой, а для обозначения чисел, меньших 10, нужно было поставить соответствующее число вертикальных штрихов. Чтобы записанные таким образом числа было легко узнавать, вертикальные штрихи иногда объединялись в группы из трех или четырех черт. Для обозначения числа 10, основания системы, египтяне вместо десяти вертикальных черт ввели новый коллективный символ, напоминающий по своим очертаниям подкову или крокетную дужку. Множество из десяти подковообразных символов, т.е. число 100, они заменили другим новым символом, напоминающим силки; десять силков, т.е. число 1000, египтяне обозначили стилизованным изображением лотоса. Продолжая в том же духе, египтяне обозначили десять лотосов согнутым пальцем, десять согнутых пальцев – волнистой линией и десять волнистых линий – фигуркой удивленного человека. В итоге древние египтяне могли представлять числа до миллиона. Самые древние из дошедших до нас математических записей высечены на камне, но наиболее важные свидетельства древнеегипетской математической деятельности запечатлены на гораздо более хрупком и недолговечном материале – папирусе. Два таких документа – папирус Ринда, или египетского писца Ахмеса (ок. 1650 до н.э.) и московский папирус, или папирус Голенищева (ок. 1850 до н.э.) – служат для нас основными источниками сведений о древнеегипетских арифметике и геометрии. В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком. В этой записи число 6789 имело вид, причем знаки более высокого порядка располагались справа, а не слева. Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.
Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления, так как дало возможность существенно сократить записи. Однако их операции с дробями продолжали оставаться на примитивном уровне, так как они знали лишь аликвотные дроби (т.е. дроби с числителем 1) и каждую дробь записывали в виде суммы аликвотных дробей, например, дробь 2/43 они записали бы так: 1/42 + 1/86 + 1/129 + 1/301. В этих системах счисления над символом, обозначающим знаменатель, ставился специальный знак. В искусстве оперирования дробями египтяне значительно уступали жителям Месопотамии.
1.2.2. Арифметика каменного века
Несколько десятков лет назад ученые-археологи обнаружили стойбище древних людей. В нем они нашли волчью кость, на которой 30 тысяч лет тому назад какой-то древний охотник нанес 55 зарубок. Видно, что, делая эти зарубки, он считал по пальцам. Узор на кости состоял из 11 групп, по 5 зарубок в каждой. При этом первые 5 групп он отделил от остальных длинной чертой. Позднее в Сибири и других были найдены сделанные в ту далекую эпоху каменного века (каменные орудия) и украшения, на которых тоже были черточки и точки, сгруппированные по 3, по 5 или по 7.
Перуанские инки вели счет животных и урожая, завязывая узелки на ремешках или шнурках разной длины и цвета . Эти узелки назывались кипу. У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают 4 узелочка ! Поэтому того, кто завязывал узелки, называли вспоминателем.
После счета по зарубкам люди изобрели особые символы, названные цифрами. Они стали применяться для обозначения различных количеств каких-либо предметов. Разные цивилизации создавали свои собственные цифры. Так, например, в древней египетской нумерации, зародившейся более 5000 лет назад, существовали особые знаки (иероглифы) для записи чисел 1, 10, 100, 1000, … Для того чтобы изобразить, например, целое число 23145, достаточно записать в ряд два иероглифа, изображающие десять тысяч, затем три иероглифа для тысячи, один – для ста, четыре – для десяти и пять иероглифов для единицы.
1.2.3. История римской системы счисления
История римской системы счисления берет свое начало, естественно, в Древнем Риме, во время расцвета Римской империи. Она применялась более двух с половиной тысяч лет назад и используется по сей день. Римскими цифрами, как основными пользовались очень долго. Еще двести лет назад во всех деловых бумагах цифры нужно было писать только римские, так как считалось, что арабские цифры гораздо проще подделать.
Сущность римской системы счисления в том, что для обозначения цифр в ней используются заглавные латинские буквы. Но немногие знают, что эти буквы выбраны неслучайно. I – обозначает один, это один палец. V- это пять, раскрытая ладонь, на которой у нас 5 пальцев. X – это десять, две скрещенные ладони, на которых у нас десять пальцев.
1.2.4 Система счисления Древней Руси
Кириллическая система счисления — система счисления Древней Руси, основанная на алфавитной записи чисел с использованием кириллицы или глаголицы.
Большинство букв древнерусского алфавита имели числовое соответствие. Так, буква «Аз» означала «один», «Веди» — «два», и т.д. Некоторые буквы числовых соответствий не имели. Числа писались и произносились слева направо за исключением чисел от 11 до 19 (например, 17 — сем-на-дцать).
По такому же принципу строилась глаголическая система счисления, в которой использовались буквы глаголицы.
В основных чертах схожа с греческой системой счисления.
Использовалась в России до начала XVIII века, когда была заменена на систему счисления, основанную на арабских цифрах.
В настоящее время используется в книгах на церковнославянском языке.
1.2.5. Различия системы счисления
Системой счисления мы будем называть способ представления числа символами некоторого алфавита, которые называют цифрами.
Причина, по которой десятичная система счисления стала общепринятой, вовсе не математическая. Десять пальцев рук – вот аппарат для счета, которым человек пользуется с доисторических времен.
Довольно широкое распространение имела двенадцатеричная система счисления. Происхождение ее тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев: всего их 12.
Особый интерес представляет так называемая «вавилонская», или шестидесятеричная, система счисления, весьма сложная система, существовавшая в Древнем Вавилоне.
Также существовали римская система счисления, египетская система счисления, китайская система счисления и другие.
Системы счисления различают:
- Анатомического происхождения: десятеричная, пятеричная, двенадцатеричная, двадцатеричная.
- Алфавитные:, древнегрузинская, древнегреческая, ионическая, славянская.
- Машинные: двоичная, восьмеричная, шестнадцатеричная.
- Прочие: Римская, Вавилонская, Египетская нумерация, Китайская нумерация и другие.
Различают позиционные и непозиционные системы счисления.
Непозиционные системы счисления возникли раньше позиционных.
Позиционные системы счисления. В позиционных системах счисления величина, обозначается цифрой, зависит от места цифры в числе. Так в числе 222 цифра 2 встречается трижды. Но самая правая означает две единицы, вторая справа – два десятка и, наконец, третья – две сотни.
Непозиционные системы счисления. В непозиционных системах счисления значение числа определяется как сумма или разность цифр в числе. В непозиционных системах счисления считать трудно. Древние греки построили геометрию, которую сегодня изучают в школе, доказали важные теоремы теории чисел, но считать они не умели. Примером непозиционный системы счисления является римская система счисления.
1.2.6. Машинная группа систем счисления
Перед математиками и конструкторами 50-х годов встала проблема отыскания таких систем счисления, которые отвечали бы требованиям, как разработчиков ЭВМ, так и создателей программного обеспечении. Одним из итогов этих исследований стало значительное изменение представлений о системах счисления и о методах вычислений. Оказалось, что арифметический счет, которым человечество пользуется с древнейших времен, может совершенствоваться, подчас весьма неожиданно и на удивление эффективно.
Специалисты выделили так называемую «машинную» группу систем счисления и разработали способы преобразования чисел этой группы. К «машинной» группе систем счисления относятся: двоичная, восьмеричная, шестнадцатеричная. Однако на начальном этапе развития информационных технологий использовалась троичная система счисления.
Некоторые идеи, лежащие в основе двоичной системы, по существу были известны в Древнем Китае. Об этом свидетельствует классическая книга (), о которой речь пойдёт позже.
Идея двоичной системы была известна и древним индусам.
В Европе двоичная система, видимо, появилась уже в новое время. Об этом свидетельствует система объёмных мер, применяемая английскими виноторговцами: два джилла = полуштоф, два полуштофа =пинта, две пинты= кварта, две кварты= потл, два потла= галлон, два галлона = пек, два пека = полубушель, два полубушеля == бушель, два бушеля = килдеркин, два килдеркина = баррель,два барреля = хогзхед, два хогзхеда = пайп, два пайпа = тан.
Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры. Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов. Звук над поверхностью воды распространялся на достаточно большое расстояние, таким образом «работал» полинезийский телеграф. В телеграфе в Х1Х-ХХ веках информация передавалась с помощью азбуки Морзе — в виде последовательности из точек и тире.
В конце XX века, века компьютеризации, Человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в двоичном виде. Каким же образом осуществляется это хранение? Каждый регистр арифметического устройства ЭВМ, каждая ячейка памяти представляет собой физическую систему, состоящую из некоторого числа однородных элементов. Каждый такой элемент способен находиться в нескольких состояниях и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый левый разряд имеет порядковый номер 0. Если при записи чисел в ЭВМ мы хотим использовать обычную десятичную систему счисления, то мы должны получать 10 устойчивых состояний для каждого разряда, как на счетах при помощи костяшек. Такие машины существуют. Однако конструкция элементов такой машины чрезвычайно сложна. Наиболее надежным и дешевым является устройство, каждый разряд которого может принимать два состояния: намагничено — не намагничено, высокое напряжение — низкое напряжение и т. д. В современной электронике развитие аппаратной базы ЭВМ идет именно в этом направлении. Следовательно, использование двоичной системы счисления в качестве внутренней системы представления информации вызвано конструктивными особенностями элементов вычислительных машин.
Обработка информации в ЭВМ основана на обмене электрическими сигналами между различными устройствами машины. Эти сигналы возникают в определенной последовательности. Признак наличия сигнала можно обозначить цифрой 1, признак отсутствия – цифрой 0. Таким образом, в ЭВМ реализуются два устойчивых состояния. С помощью определенных наборов цифр 0 и 1 можно закодировать любую информацию. Каждый такой набор нулей и единиц называется двоичным кодом.
1.3. Проведение анкетирования
Опрос проводили среди учеников 8-11классов
Письменный опрос.
Информация в ЭВМ координируется:
в двоичной системе счисления;
в десятичной системе счисления;
в символах.
Система счисления – это
представление чисел в экспоненциальной форме;
представление чисел с постоянным положением запятой;
способ представления чисел с помощью символов, имеющих определенные количественные значения.
В зависимости от способа изображения чисел системы счисления делятся на:
позиционные и не позиционные;
арабские и римские;
древние и современные;
представленные в виде ряда и в виде разрядной сетки.
Двоичная система счисления имеет основание Р=:
0; 2;
1.
Для представления чисел в восьмеричной системе счисления используют цифры:
0,1,2,3,4,5,6,7,8;
0,1,2,3,4,5,6,7;
1,2,3,4,5,6,7,8.
Для перевода чисел из одной системы счисления в другую существует:
таблицы перевода;
правила перевода;
соответствующие стандарты.
Первое понятие системы счисления появилось:
в глубокой древности, точно сказать сложно;
за 500 лет до н.э.;
до начала X века н.э.
2. Проведение исследования
2.1. Первый этап исследования
На первом этапе исследования я сравнила системы счисления разных времен и народов.
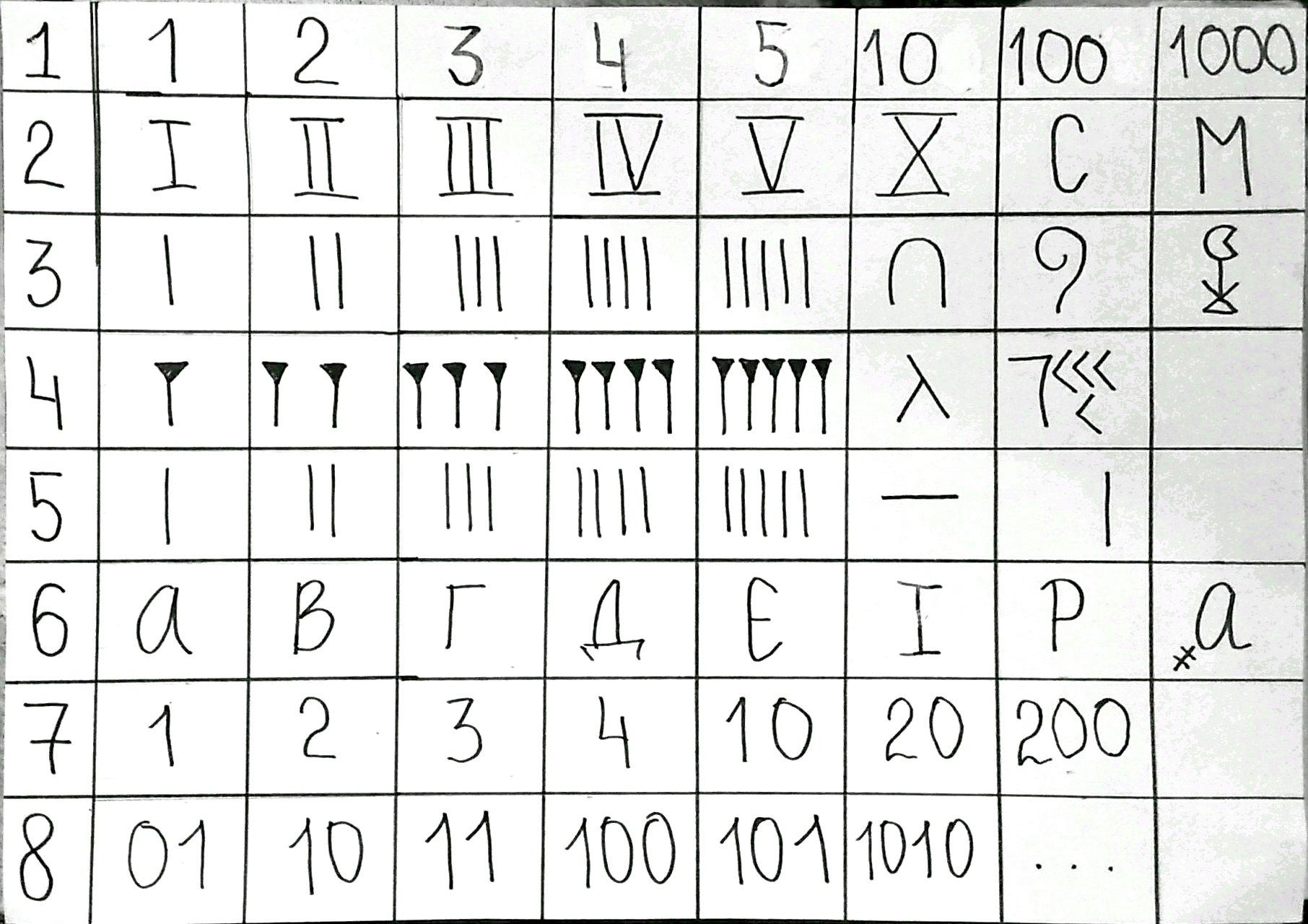
Десятичная система счисления - позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
Римская система счисления - цифры, использовавшиеся древними римлянами в их непозиционной системе счисления. Натуральные числа записываются при помощи повторения этих цифр. При этом, если большая цифра стоит перед меньшей, то они складываются (принцип сложения), если же меньшая стоит перед большей, то меньшая вычитается из большей (принцип вычитания). Последнее правило применяется только во избежание четырёхкратного повторения одной и той же цифры.
Римские цифры появились за 500 лет до нашей эры у этрусков, которые могли заимствовать часть цифр у прото-кельтов.
Египетская система счисления - непозиционная система счисления, которая употреблялась в Древнем Египте вплоть до начала X века н.э. В этой системе цифрами являлись иероглифические символы; они обозначали числа 1, 10, 100 и т. д. до миллиона. Появилась такая система счисления около 2850 до н.э.
Вавилонская система счисления - является позиционной, возникла за тысячи лет до наступления новой эры и была началом начала математики. Несмотря на свой древнейший возраст, она поддалась расшифровке и раскрыла исследователям множество тайн Древнего Востока.
Система счисления Древнего Китая (палочковая). Одна из древнейших систем счисления была создана в Китае, а также в Японии. Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску.
Система счисления Древней Руси - кириллическая система счисления, основанная на алфавитной записи чисел с использованием кириллицы или глаголицы.
В основных чертах схожа с греческой системой счисления. Использовалась в России до начала XVIII века, когда была заменена на систему счисления, основанную на арабских цифрах.
В настоящее время используется в книгах на церковнославянском языке.
Пятеричная система счисления - позиционная система счисления с основанием 5. По свидетельству известного исследователя Африки Стенки, у ряда африканских племен была распространена пятеричная система счисления. Долгое время пользовались пятеричной системой счисления и в Китае. Очевидна связь этой системы со строением человеческой руки. В ней используются цифры: 0,1,2,3,4.
Двоичная система счисления - позиционная система счисления с основанием 2. Благодаря непосредственной реализации в цифровых электронных схемах на логических вентилях, двоичная система используется практически во всех современных компьютерах и прочих вычислительных электронных устройствах.
2.2. Второй этап исследования
Письменный опрос
На втором этапе проведем анализ опроса среди 120 учеников школы.
Из них абсолютно правильно на вопросы ответили всего лишь 11 учеников.
Информация в ЭВМ координируется:
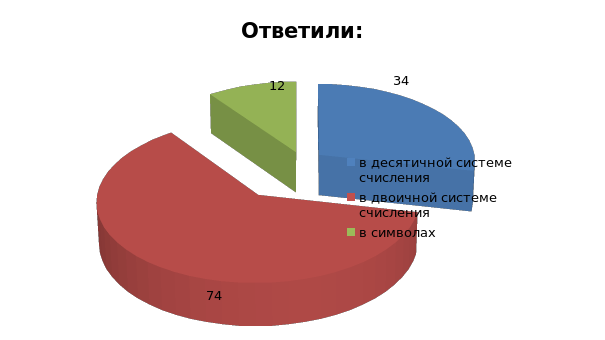
Правильный ответ: в двоичной системе счисления
Система счисления – это
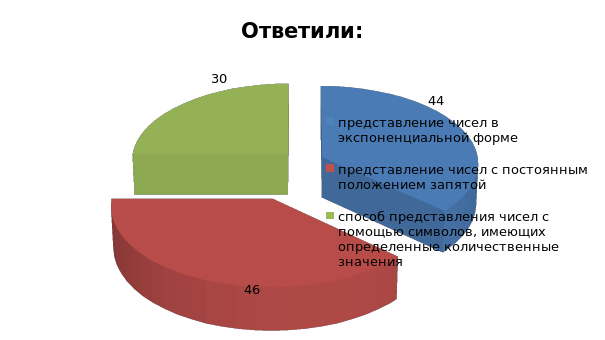
Правильный ответ: способ представления чисел с помощью символов, имеющих определенные количественные значения
В зависимости от способа изображения чисел системы счисления делятся на:

Правильный ответ: позиционные м непозиционные
Двоичная система счисления имеет основание Р=:
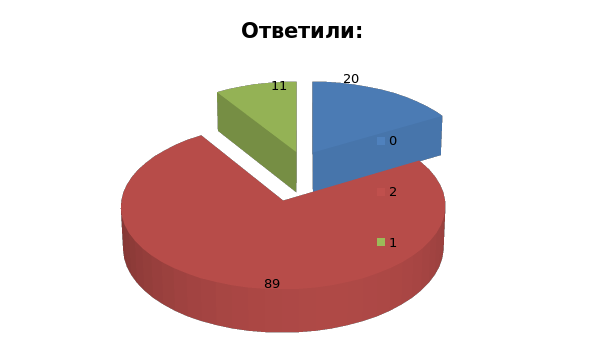
Правильный ответ: 2
Для представления чисел в восьмеричной системе счисления используют цифры:
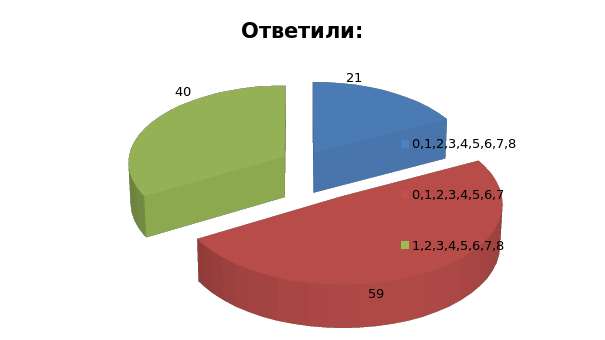
Правильный ответ: 0,1,2,3,4,5,6,7
Для перевода чисел из одной системы счисления в другую существует:
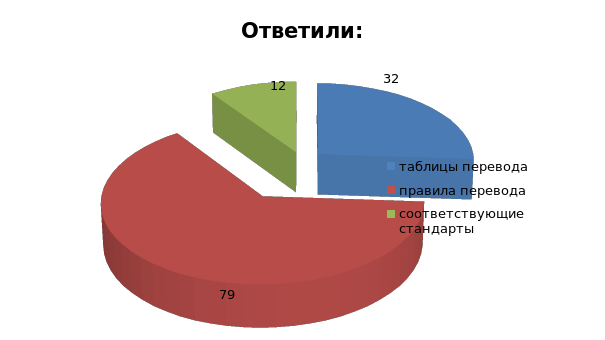
Правильный ответ: таблицы перевода
Первое понятие системы счисления появилось:
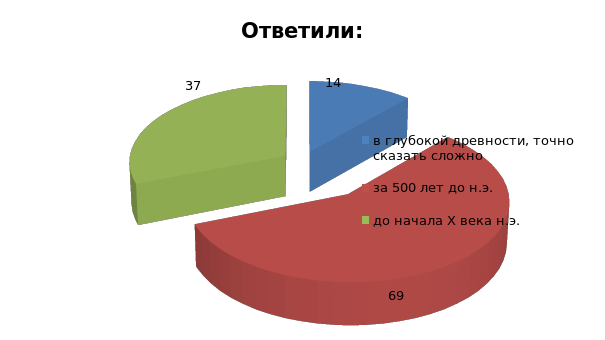
Правильный ответ: в глубокой древности, точно сказать сложно
2.3. Заключительный этап исследования
Общие итоги анкетирования.
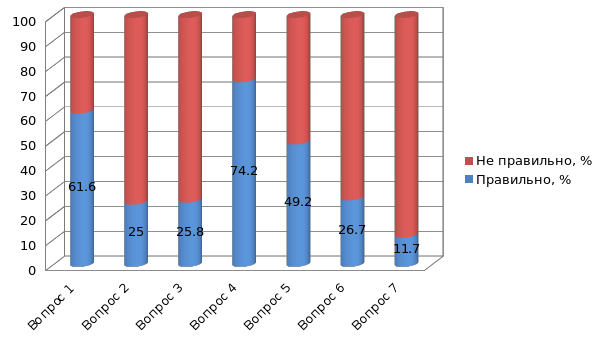 И так, из результатов опроса видно, что не смотря на то, что люди с самых малых лет научились считать и пользоваться числами, не многие смогут ответить на вопрос откуда же они взялись и на сколько давно появились.
И так, из результатов опроса видно, что не смотря на то, что люди с самых малых лет научились считать и пользоваться числами, не многие смогут ответить на вопрос откуда же они взялись и на сколько давно появились.
Искусство счета развивалось с развитием человечества. Способов счета было придумано немало: зарубки на палке, узлы на веревке, складывание в кучу камешков. Но носить все это с собой неудобно. И тут на помощь приходят пальцы рук. А если предметов больше 10? Тогда люди придумали десятичную систему счисления, которой мы пользуемся до сих пор. «Пальцевое» происхождение десятичной системы счисления подтверждается формой римских цифр: цифра пять (V) - ладонь с оттопыренным большим пальцем, а цифра десять (Х)- две скрещенные руки.
Заключение
В ходе изучения данной темы мы выяснили, что двоичная система счисления намного старше электронных машин. Двоичной системой счисления люди интересуются давно. Знаменитый Лейбниц считал двоичную систему счисления простой, удобной, красивой.
Двоичная система счисления наиболее проста и удобна для автоматизации.
Наличие в системе всего лишь двух символов упрощает их преобразование в электрические сигналы.
Из любой системы счисления можно перейти к двоичному коду.
Почти все ЭВМ используют либо непосредственно двоичную систему счисления, либо двоичное кодирование какой-либо другой системы счисления.
Но двоичная система имеет и недостатки:
- ею пользуются только для ЭВМ для внутренней и внешней работы;
- быстрый рост числа разрядов, необходимых для записи чисел.
Проследив основные этапы зарождения чисел, их различных систем записей у ранних народов, необходимо сделать вывод:
Не зря многие ученые умы интересовались понятием числа, раскрывали его тайны. Да и в наш век, когда с числами сталкиваемся повсеместно, это понятие не утратило своей актуальности. Трудно себе представить как современный человек смог бы прожить, если бы когда-то много тысячелетий назад, не было бы приоткрыто тайна великих и загадочных чисел.
Список литературы
Система счисления и их применение/ С.Б. Гашков/ Москва-2004
Основы информатики: Учебник для вузов/ Беляев М.А., Лысенко В.В., Малинина Л.А. - 2006
Библиотека сайта «Инфоурок» - https://infourok.ru/biblioteka
Сайт «Русь Былинная» - http://wikii.ru/, http://wikii.ru/publ/obo_vsem/sistema_schislenija_drevnej_rusi/28-1-0-2073
Свободная энциклопедия «Викиредия» - https://ru.wikipedia.org
Библиотека сайта «Мегакнига» - http://megapredmet.ru/1-69177.html
Счет и число/ Берман Н.Г/. ОГИЗ Гостехиздат/ Москва
Детская энциклопедия «Я познаю мир»/ «Астрель»/ Москва - 2004














 И так, из результатов опроса видно, что не смотря на то, что люди с самых малых лет научились считать и пользоваться числами, не многие смогут ответить на вопрос откуда же они взялись и на сколько давно появились.
И так, из результатов опроса видно, что не смотря на то, что люди с самых малых лет научились считать и пользоваться числами, не многие смогут ответить на вопрос откуда же они взялись и на сколько давно появились.









