Аннотация
«Методы решения задач с параметром».
г. Северобайкальск «МАОУ Лицей №6» 11 класс
Актуальность обосновывается стремлением к нахождению простых способов решения задач повышенного уровня сложности, а также желанием каждого старшеклассника сдать ЕГЭ на высший балл.
Цель работы заключается в исследование методов решения задач с параметром и выявление наиболее рациональных, наименее трудоемких способов решения.
Для достижения поставленной цели необходимо решить следующие задачи:
1. познакомится с видами задач с параметром;
2. исследовать способы решения задач с параметром и постараться выбрать из них для себя самые оптимальные;
3. приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике.
Гипотеза моего исследования заключается в том, что существуют общие методы решения заданий с параметром, позволяющие решать задачи разных видов.
Объект исследования: задания контрольно-измерительных материалов единого государственного экзамена по математике на задачи с параметром.
Выводы: Не верьте тем, кто говорит, что задание 18 Профильного ЕГЭ по математике (задачи с параметром) решить невозможно. Это не так. Его можно решить, если знать какой ключик необходимо подобрать, чтобы заветные 4 балла упали в вашу копилку.
МАОУ «Лицей №6»
Исследовательская работа на тему:
«Методы решения задач с параметрами».
Работу выполнила:
Барахтина Софья
ученица 11 класса
Руководитель проекта:
Ларькова
Татьяна Павловна
Учитель математики
г. Северобайкальск
2023 год.
Оглавление
Введение. - 3 -
1. Теоретическая часть. - 4 -
1.1 Основные понятия и термины. - 4 -
1.2 Основные типы задач с параметрами на ЕГЭ. - 4 -
1.3 Виды уравнений с параметром - 5 -
1.4 Основные способы (методы) решения задач с параметром: - 6 -
1.4.1 Аналитический способ. - 6 -
1.4.2 Графический способ. - 8 -
1.4.3 Функциональный способ. - 10 -
2.Практическая часть. - 11 -
2.1 Примеры решения заданий №18 ЕГЭ - 11 -
Заключение. - 15 -
Список использованной литературы и интернет ресурсов. - 16 -
Введение.
Некоторые ученики при решении задач с параметрами сталкиваются с большими трудностями, а многие и вовсе не приступают к заданию, даже несмотря на то, что оно высоко оценивается, считая его невыполнимым.
Актуальность обосновывается стремлением к нахождению простых способов решения задач повышенного уровня сложности, а также желанием каждого старшеклассника сдать ЕГЭ на высший балл.
Цель работы заключается в исследование методов решения задач с параметрами и выявление наиболее рациональных, наименее трудоемких способов решения.
Для достижения поставленной цели необходимо решить следующие задачи:
1. Познакомится с видами задач с параметрами;
2. Исследовать способы решения задач с параметрами и постараться выбрать из них для себя самые оптимальные;
3. Приобрести опыт в решении задач, содержащиеся в ЕГЭ по профильной математике.
Гипотеза моего исследования заключается в том, что существуют общие методы решения заданий с параметрами, позволяющие решать задачи разных видов.
Объект исследования: задания контрольно-измерительных материалов единого государственного экзамена по математике на задачи с параметрами.
Предмет исследования: методы решения задач с параметрами.
Методы исследования – теоретический анализ и синтез научной и учебной литературы по теме исследования, сравнение, систематизация информации, обобщение, вывод, подбор и решение задач.
Практическая значимость – возможность использования обобщенных данных при подготовке выпускников к сдаче единого государственного экзамена по математике профильного уровня, отработка решения задач с параметрами.
1. Теоретическая часть. 1.1 Основные понятия и термины.
Параметром называется независимая переменная, значение которой в задаче считается заданным фиксированным или произвольным действительным числом, или числом, принадлежащим заранее оговоренному множеству.
Уравнение (неравенство) с параметрами — это математическое уравнение (неравенство), внешний вид и решение которого зависит от значений одного или нескольких параметров.
Решить задачу с параметром - предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству (уравнение) или поиске указанных значений параметра (удовлетворение заданному условию).
1.2 Основные типы задач с параметрами на ЕГЭ.
Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.
Это базовый тип задач, на котором строятся остальные типы задач.
Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).
Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений.
Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
1.3 Виды уравнений с параметром
1) Рациональные уравнения с параметром.
Пример: Найдите все значения 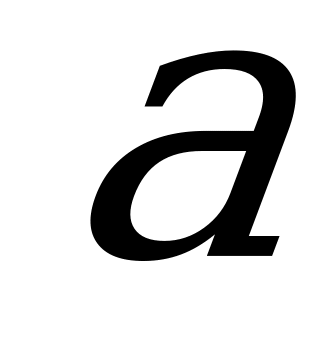 , при которых уравнение
, при которых уравнение
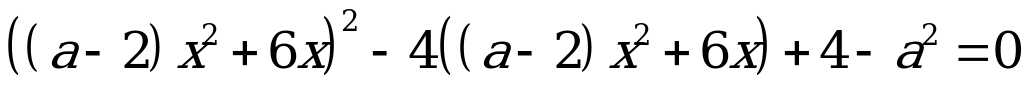 имеет ровно два решения.
имеет ровно два решения.
2) Дробно-рациональные уравнения с параметром.
Пример: Найдите все значения a, при каждом из которых уравнение
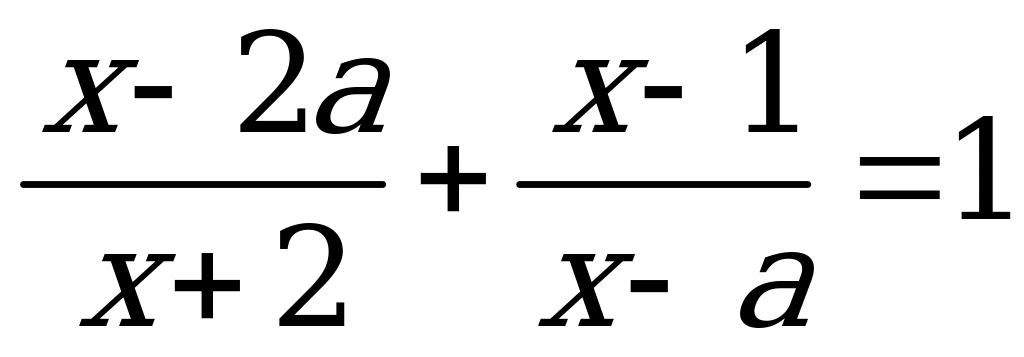 имеет ровно один корень.
имеет ровно один корень.
3) Уравнения с параметром, содержащие корни.
Пример: Найдите все значения a, при каждом из которых уравнение
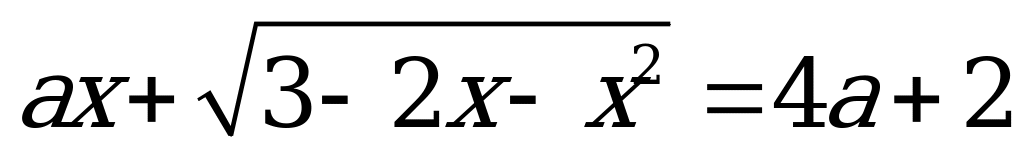 имеет единственный корень.
имеет единственный корень.
4) Уравнения с параметром, содержащие модуль.
Пример: Найдите все значения 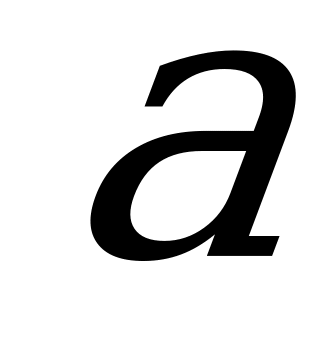 , при которых уравнение
, при которых уравнение 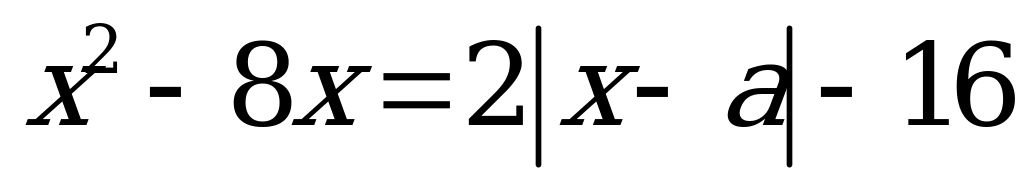 имеет ровно три решения.
имеет ровно три решения.
5) Тригонометрические уравнения с параметром.
Пример: Найдите все значения 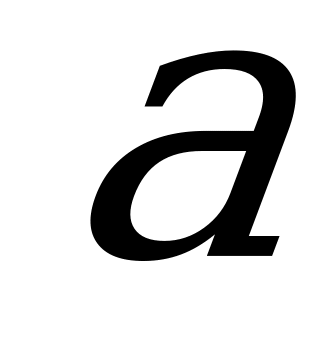 , при каждом из которых уравнение
, при каждом из которых уравнение
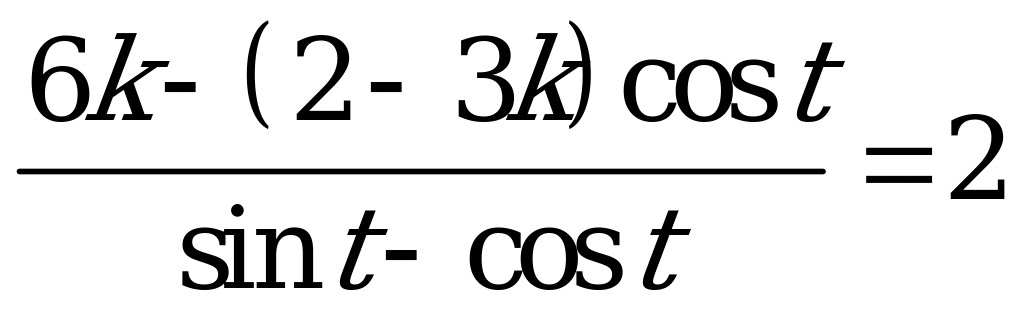 имеет хотя бы одно решение на отрезке
имеет хотя бы одно решение на отрезке 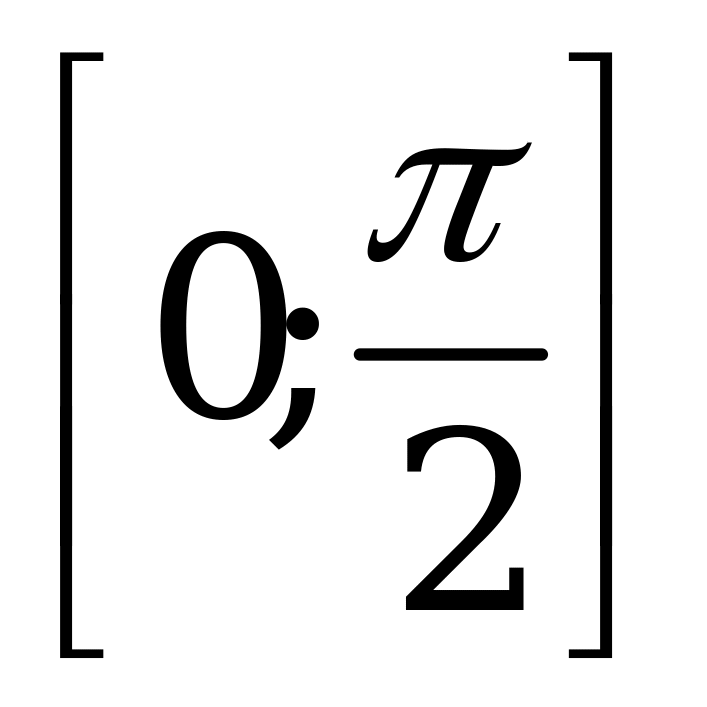 .
.
6) Показательные уравнения с параметром.
Пример: Найдите все значения 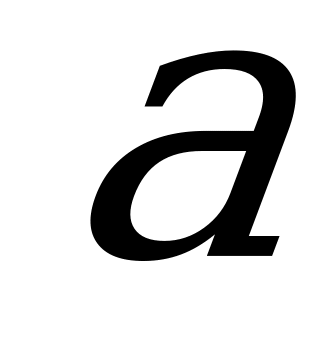 , при каждом из которых уравнение
, при каждом из которых уравнение
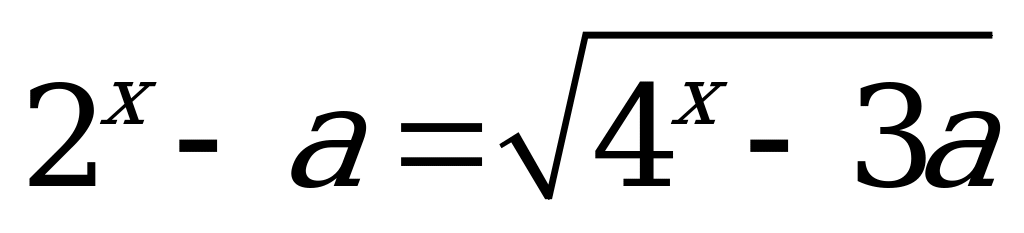 имеет единственный корень. 4
имеет единственный корень. 4
7) Логарифмические уравнения с параметром.
Пример: При каких значениях параметра 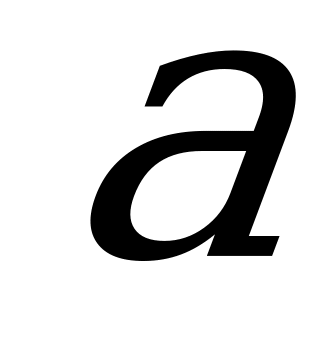 уравнение
уравнение 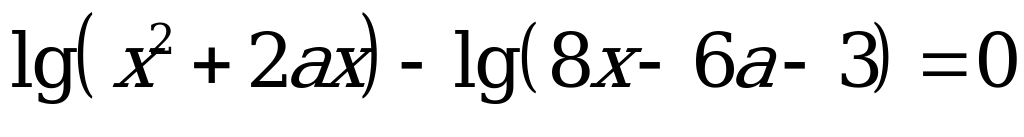 имеет единственное решение.
имеет единственное решение.
1.4 Основные способы (методы) решения задач с параметром: 1.4.1 Аналитический способ.
Это способ прямого решения, повторяющий алгоритм нахождения ответа в задачах без параметра.
Пример: Найдите все значения параметра a, при которых уравнение:
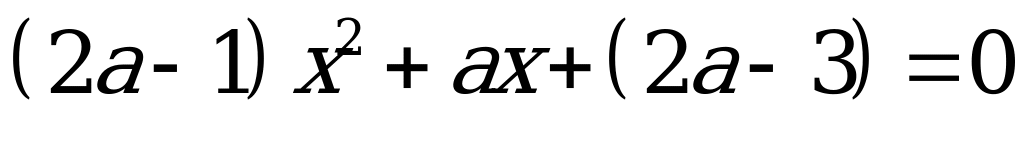 имеет не более одного корня.
имеет не более одного корня.
Решение:
чтобы оно имело не более одного корня необходимо и достаточно, чтобы дискриминант был не положителен:
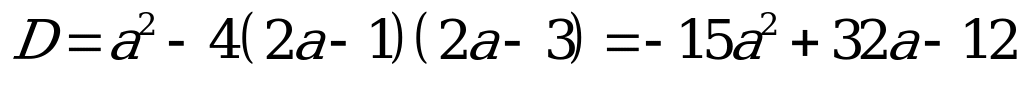
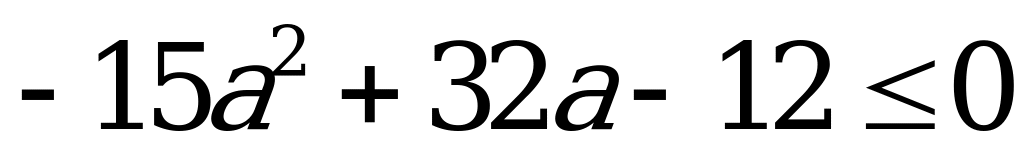 ,
, 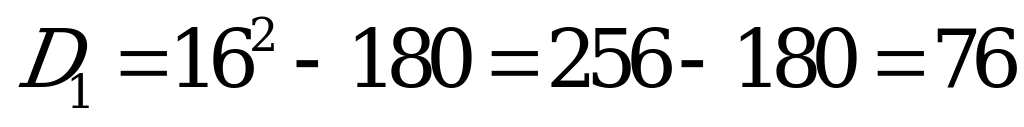
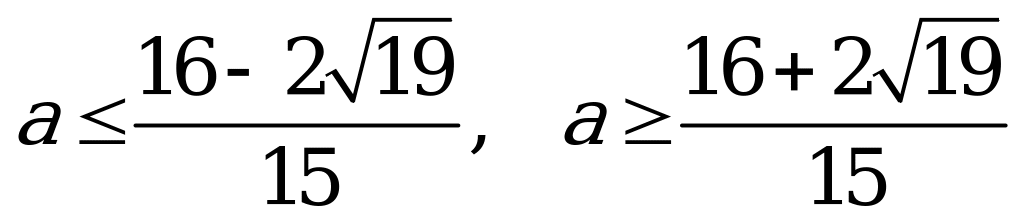
чтобы записать окончательный ответ, необходимо сравнить  и числа
и числа
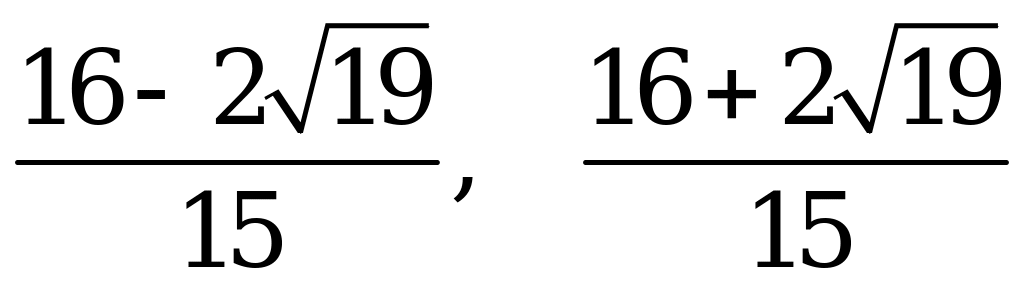
Ответ: 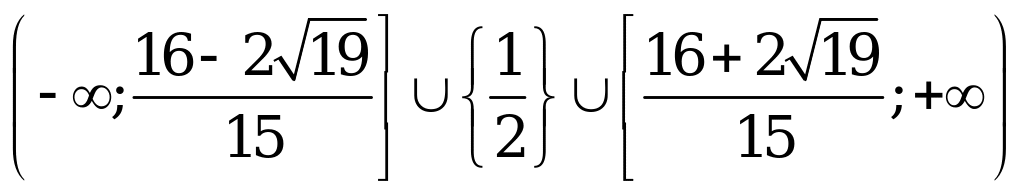
В таблице приведена полная система случаев расположения корней уравнения в зависимости от значений выражений, зависящих от коэффициентов уравнения.
| 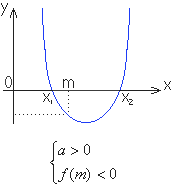 | один корень меньше m, а другой больше Условие a 0 обеспечивает положительный коэффициент перед x2 (направленность ветвей параболы вверх) Условие f (m) наличие корней квадратного трехчлена расположение точки m между корнями |
| 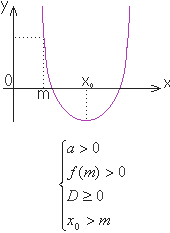 | оба корня больше m Условие a 0 обеспечивает положительный коэффициент перед x2 Условие f (m) 0 обеспечивает расположение точки m вне отрезка между корнями Условие D  0 обеспечивает наличие корней уравнения 0 обеспечивает наличие корней уравнения Условие x0 m обеспечивает расположение точки m левее отрезка между корнями |
| 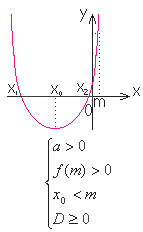 | оба корня меньше m Условие a 0 обеспечивает положительный коэффициент перед x2 Условие f (m) 0 обеспечивает расположение точки m вне отрезка между корнями Условие D  0 обеспечивает наличие корней уравнения 0 обеспечивает наличие корней уравнения Условие x0 |
1.4.2 Графический способ.
Это способ решения, основанный на построении и исследовании геометрической модели данной задачи.
Алгоритм решения задачи с параметром графическим способом состоит из следующих шагов:
1. Разбиваем задачу на несколько «простых функций».
2.Строим в одной системе координат все графики получившихся уравнений.
3.Находим точки пересечения.
4.Считываем нужную информацию.
Также стоит помнить основные графики функций и правила их преобразования:
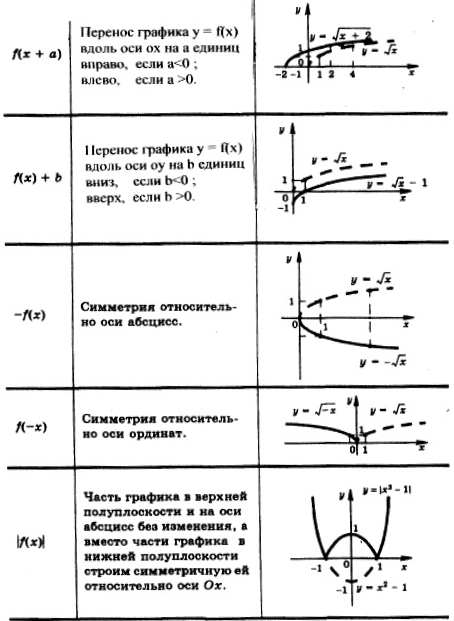
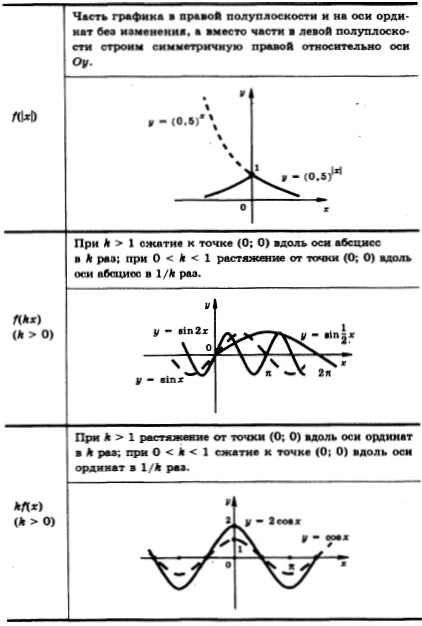
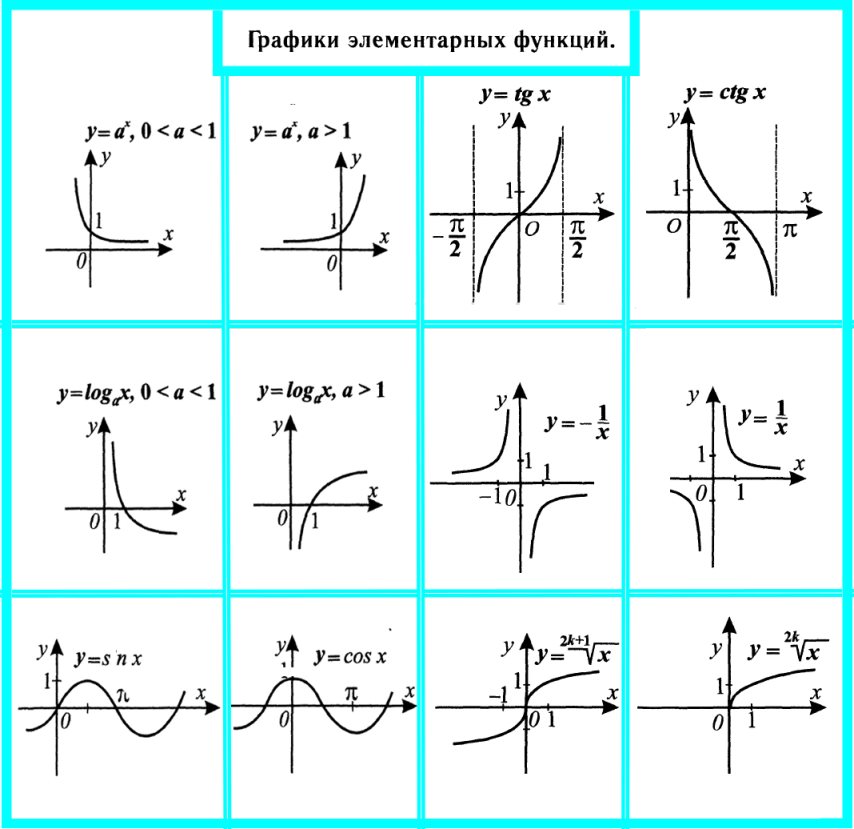
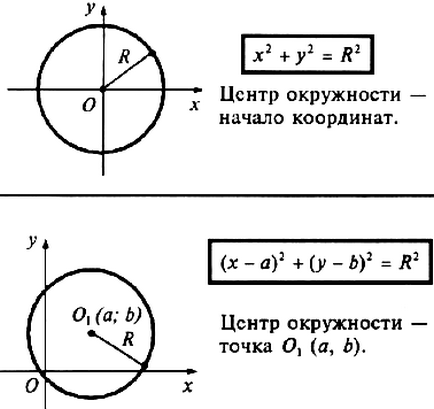
Пример: Найдите все значения параметра а при каждом из которых уравнение: │х2-4х+3│=3а-2а2 имеет ровно 4 различных решения.
Р ешение: рассмотрим данное уравнение как систему, состоящую из 2 функций: у1=│х2-4х+3│
ешение: рассмотрим данное уравнение как систему, состоящую из 2 функций: у1=│х2-4х+3│
у2=3а-2а2, где первая функция — это парабола, а вторая- прямая.
Построим график функций первого уравнения, для этого найдем вершину параболы и точки пересечения с осью ох: вершина параболы (2; -1), и точки пересечения это 1 и 3. И так как выражение под модулем перевернём график там, где функция меньше 0.
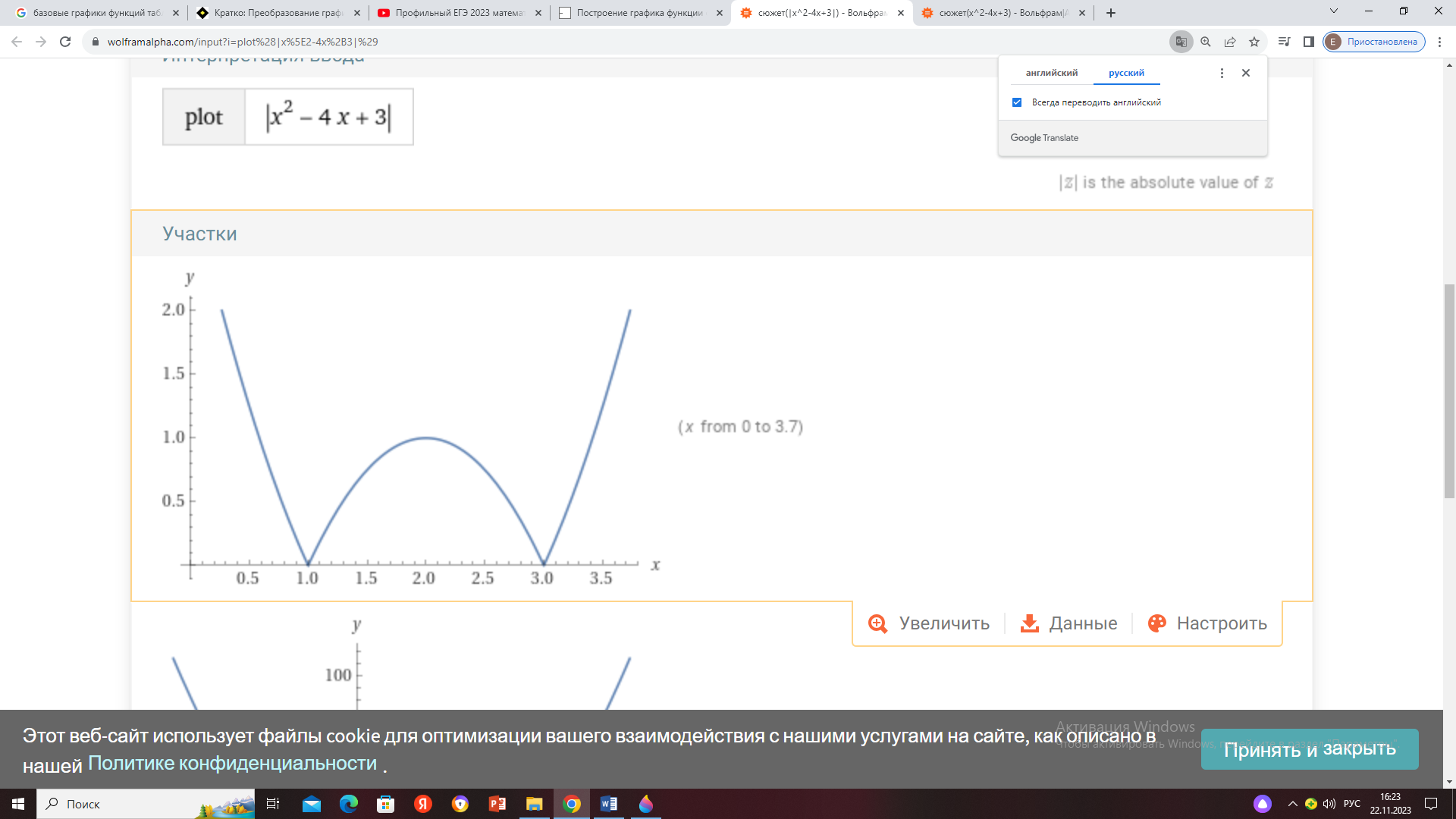
Так как вторая функция это прямая паралельная оси ох, мы можем записать что у=к, тогда нам нужно понять на каком участке выполняется данное условие (4 точки пересечения), на рисунке наглядно видно что это условие выполняется при к € (0;1)
З
 начит мы можем записать что: 03а-2а2
начит мы можем записать что: 03а-2а2
0 3а-2а2; а € (0; 1,5)
3а-2а2; а € (0; 1,5)
3а-2а2€ (-∞; 0,5) (0,5; ∞) Ответ: а € (0; 0,5) (0,5; 1,5)
1.4.3 Функциональный способ.
Это способ, в котором базовым является исследование некоторой функции. Чаще всего при его использований графики функций строят в координатной плоскости с осями (х;а). В данном способе ответ сразу считывается с графического изображения.
Алгоритм решения задачи с параметром
функциональным способом:
Выражаем параметр через другие переменные.
2. Строим графики функций с системе координат (х;а).
3. Считываем нужную информацию.
Пример: Найдите все значения параметра а, при каждом из которых уравнение: 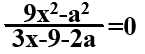 , имеет ровно 2 различных решения.
, имеет ровно 2 различных решения.
Решение: в дробно-иррациональных уравнениях первый шаг в решении — это всегда запись ОДЗ!
Запишем ОДЗ для нашего случая:
3х-9-2а ≠0; х≠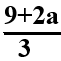 ,
,
Д
 алее мы можем составить систему уравненй, выражая а через х:
алее мы можем составить систему уравненй, выражая а через х:
9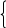 х2-а2=0 9х2=а2 а=± 3а
х2-а2=0 9х2=а2 а=± 3а
3х-9-2а ≠0 3х-9 ≠2а а≠3х-9/2, перенесём все прямые на общий график:
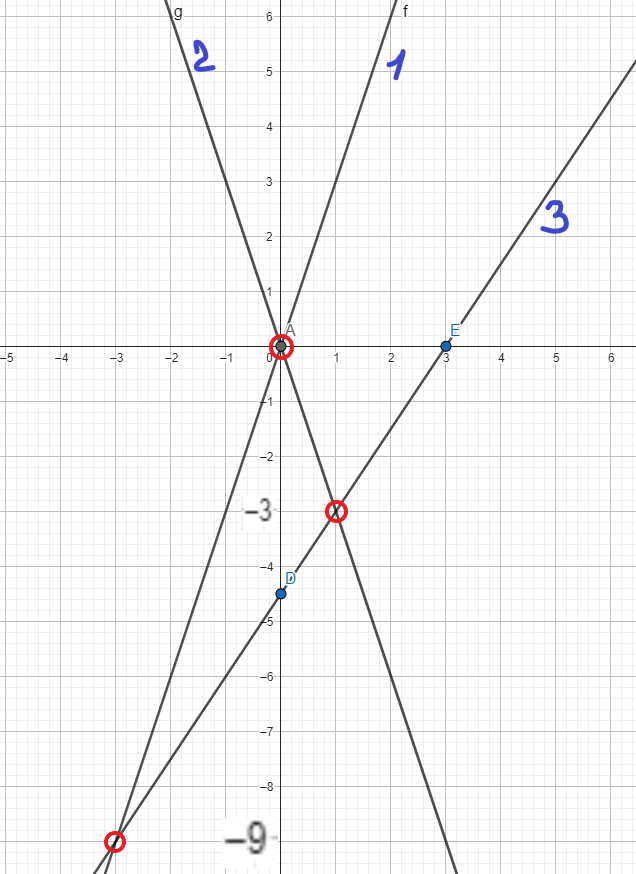
На графике явно видно решения задачи.
Ответ: а € (-∞;-9) ⋃ (-9; -3) ⋃ (-3; 0) ⋃ (0; ∞)
Примечание: самый быстрый способ решения данной задачи
2.Практическая часть. 2.1 Примеры решения заданий №18 ЕГЭ
Рассмотрим примеры решения заданий из банка ФИПИ:
№1. Найдите значения, а при каждом из которых решения неравенства: │2х-а│+1≤│х+3│, образуют отрезок длины 1.
Примечание: На решение данной задачи аналитическим методом уйдет очень много времени (1,2 часа), а геометрическим методом эту задачу можно решить гораздо быстрее (0,5 часа)
Решение: Преобразуем неравенство так, чтобы с лева осталось только выражение с параметром
│2х-а│≤ │х+3│-1
Д алее решаем систему уравнений: где оба уравнения линейные
алее решаем систему уравнений: где оба уравнения линейные
у1=│2х-а│
у2=│х+3│-1
Сначала построим график 2 функции так как она не зависит от параметра.
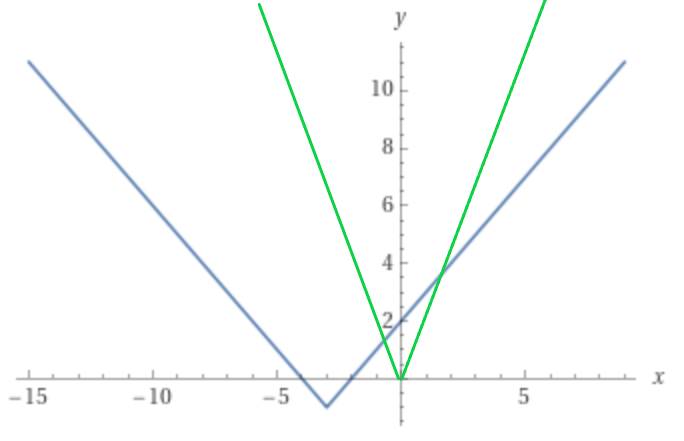
Рассмотрим как будет выглядеть график 2 фунции. Например при а=0. Для того чтобы удовлетворить условие неравенства нам нужно чтобы график функций 1 был ниже графика 2. Из рисунка понятно что такое может произойти 2 раза (меньше правой ветки и меньше левой ветки). Схематически изобразим эти 2 случая.

Т
 еперь поняв какие варианты возможны, приступаем к решению задачи. Условия задачи: образуют отрезок длинны 1 означает х2-х1=1. Запишем 2 сисемы уравнений удовлетворяющих условию:
еперь поняв какие варианты возможны, приступаем к решению задачи. Условия задачи: образуют отрезок длинны 1 означает х2-х1=1. Запишем 2 сисемы уравнений удовлетворяющих условию:
х 2-х1=1 х2-х1=1 х2-х1=1 х2=-1,5 а1=-2,5
2-х1=1 х2-х1=1 х2-х1=1 х2=-1,5 а1=-2,5
2х1-а=х1+3-1 х1=а+2 х1-3х2=4 (Случай 1)
а -2х2=х2+3-1 -3х2=2-а
-2х2=х2+3-1 -3х2=2-а
 х2-х1=1 х2-х1=1 х2-х1=1 х1=-4,5 а2=-9,5
х2-х1=1 х2-х1=1 х2-х1=1 х1=-4,5 а2=-9,5
-х1-3-1=2х1-а 3х1=а-4 3х1-х2=-8 (Случай 2)
-х2-3-1=а-2х2 х2=а+4
Ответ: а=-2,5; а=-9,5
Плюсы геометрического подхода к решению в этой задаче состоят в том, что глядя на рисунок наглядно понятно с каким знаком нужно раскрывать модуль (идём по правой ветке раскрываем с +; по левой с -)
№2. Найдите все значения а при каждом из которых решение уравнения: а2-9х2+18│х│-9=0, имеет ровно 2 различных корня.
Примечание: При решении задачи данным способом ответ буквально виден на графике, его только остается записать.
Решение:
Преобразуем уравнение для перехода в систему координат (х;а)
а2=9х2-18│х│+9, вынесем 9 за скобки
а2=9 (х2-2│х│+1), заметим в скобках ФСУ (также помним, что│х2│=х2)
а2=9 (│х2│-2│х│+1)
а 2=32 (│х│-1)2, такое возможно только в двух случаях:
2=32 (│х│-1)2, такое возможно только в двух случаях:
а1=3 (│х│-1); (Функция 1)
а2=-3 (│х│-1); (Функция 2), построим графики этих функций на координатной плоскости (х;а).
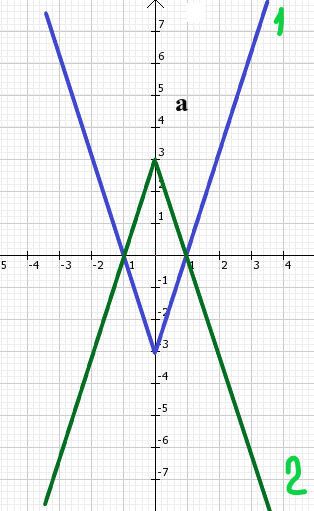
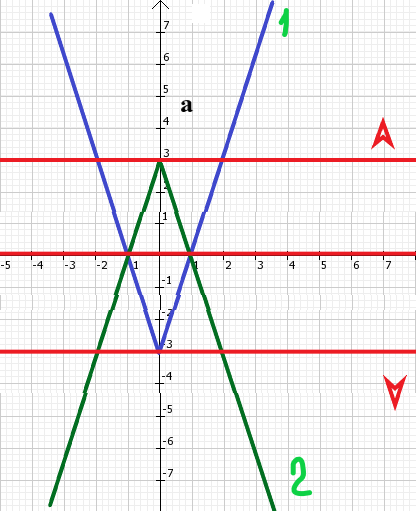
На рисунке наглядно видно при каких значениях а система графиков имеет ровно 2 решения.
О
 твет: а € (-∞;3) ⋃ 0 ⋃ (3; ∞)
твет: а € (-∞;3) ⋃ 0 ⋃ (3; ∞)
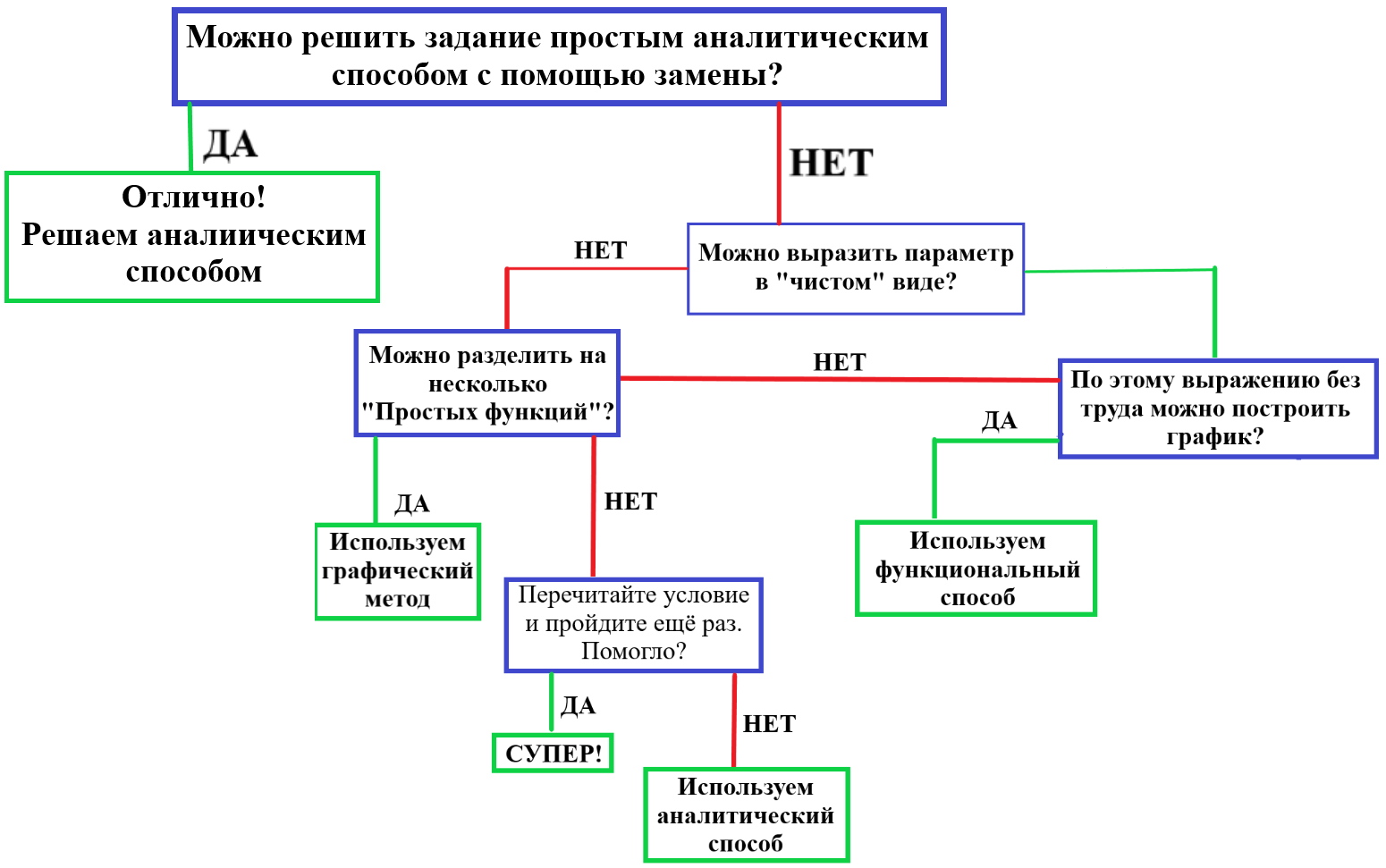
Основные подходы, применяемые при решении задания №18 ЕГЭ:
Внимательно прочитать условие.
Выбрать менее трудоёмкий способ решения задач с параметром.
Если задание можно разделить на 2 «простых» уравнения, то стоит выбрать геометрический способ.
Если в задании параметр явно можно выразить как функцию, то стоит выбрать способ «относительно параметра».
Также в качестве практической работы мной был разработан сборник заданий для самостоятельного решения на математических кружках для учащихся 10-11 классов по теме: «Методы решения задач с параметрами» (Приложение 1).
Заключение.
1. В работе изложены основные понятия и методы для решения 18 задания ЕГЭ на задачи с параметрами.
2. На примерах проиллюстрировано применение различных методов для решения задач с параметрами.
3. Составлены основные подходы для решения заданий с параметрами.
4. Составлен сборник заданий с материалом, который может быть использован при подготовке к ЕГЭ по математике.
Список использованной литературы и интернет ресурсов.
СдамГИА/РешуЕГЭ – образовательный портал для подготовки к
экзаменам.
Банк заданий ФИПИ.
А. Шахмейстер «Задачи с параметрами в ЕГЭ» – «Петроглиф», №1 2004 г.
Е.А.Ефимов «Задачи с параметром» – Самарский гос. аэрокосмический университет, 2006г.
П.И. Горнштейн, В.Б. Полонский, М.С. Якир «Задачи с параметрами» – РИА, 2002г.
https://ege.sdamgia.ru/
https://2.shkolkovo.online/catalog/1645?SubjectId=1
Рецензия
Барахтиной Софьи Александровны,
учащейся 11а класса МАОУ «Лицей №6»
Тема проекта: «Методы решения задач с параметрами».
Предмет: Математика. Профиль. Подготовка к ЕГЭ.
Вид проекта: исследовательская работа.
Работа, представленная Барахтиной Софьей, заключается в исследовании методов решения одной из наиболее сложных задач Единого Государственного экзамена по профильной математике - решения задач с параметрами. К заданиям такого типа приступает небольшое количество учеников, так как многие считают ее сложно выполнимой. Актуальность работы обосновывается стремлением к нахождению простых способов решения задач повышенного уровня сложности. Тема работы отражает содержание проекта, подробно рассматриваются типы задач, виды уравнений, основные способы решений задач с параметром. Приведены примеры решения таких задач.
Данная работа отвечает требованиям, предъявляемым к содержанию и оформлению индивидуального итогового проекта выпускника 11 класса. Автором проекта была четко определена цель работы, поставлены задачи, аргументирована актуальность темы, грамотно подобраны методы работы, сформулирована практическая значимость. Софья продемонстрировала умение самостоятельно работать с различными источниками информации, делать обобщения и выводы, планировать выступление.
Структура проекта соответствует требованиям, содержит в себе титульный лист, оглавление, введение, основную часть, заключение, список литературы. В основной части проекта содержит обширный теоретический материал и его анализ, практическая часть.
В практической части представлены примеры решения заданий с параметром. Также автором работы был разработан сборник заданий для самостоятельного решения на математических кружках для учащихся 10-11 классов по теме: «Методы решения задач с параметрами».
Работа отвечает требованиям к содержанию и оформлению итогового индивидуального проекта и рекомендуется к защите.
Рецензент: Ларькова Т. П.
учитель математики
14.04.2024
21







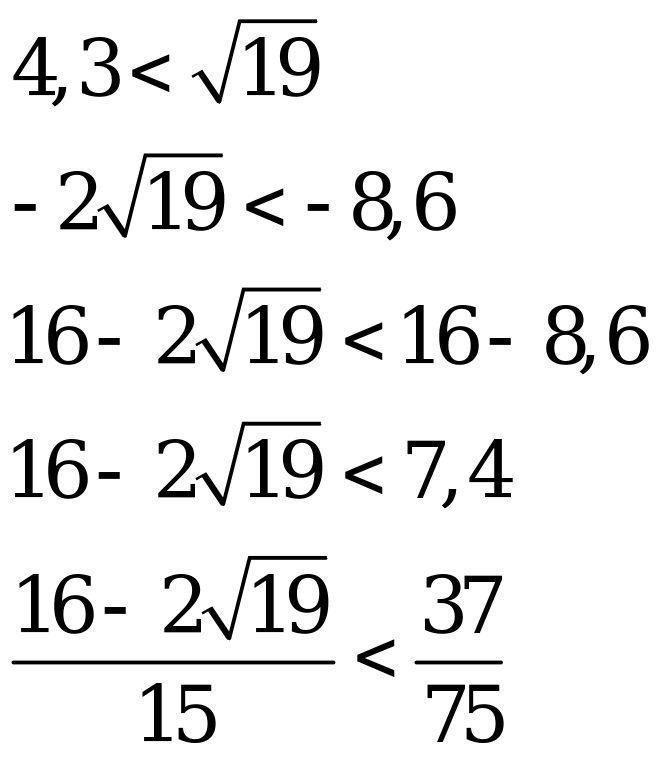
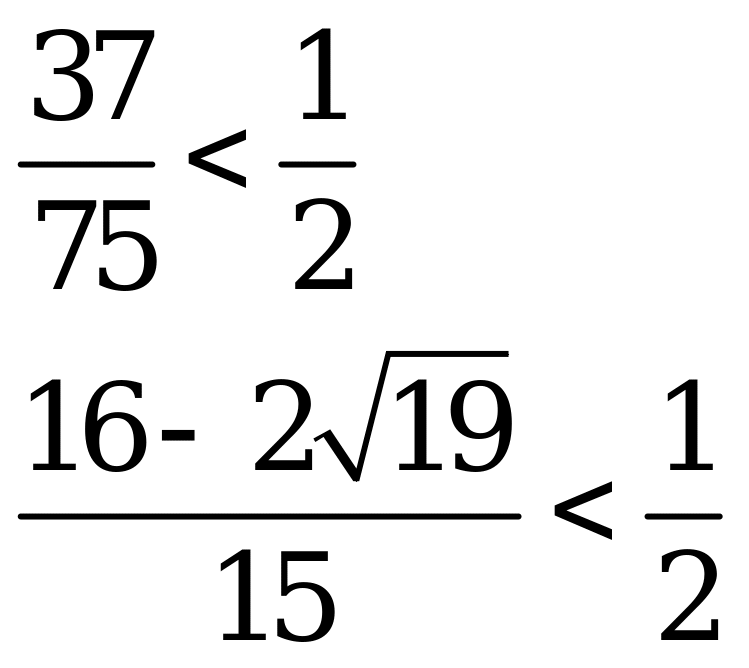
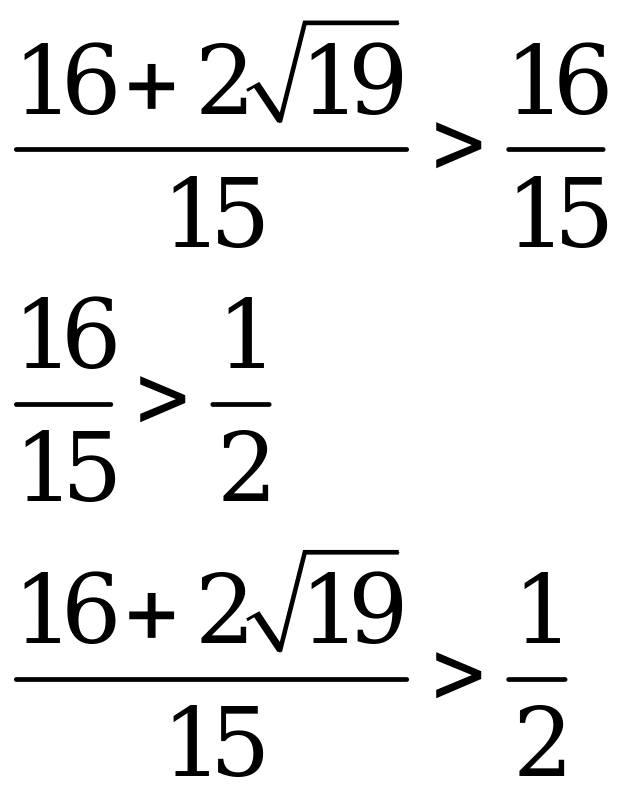
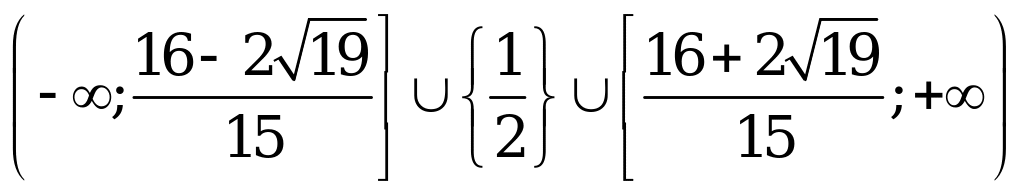

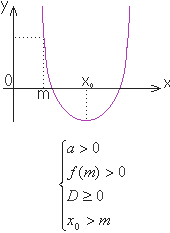
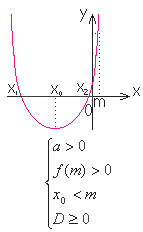




 ешение: рассмотрим данное уравнение как систему, состоящую из 2 функций: у1=│х2-4х+3│
ешение: рассмотрим данное уравнение как систему, состоящую из 2 функций: у1=│х2-4х+3│


 начит мы можем записать что: 03а-2а2
начит мы можем записать что: 03а-2а2  3а-2а2; а € (0; 1,5)
3а-2а2; а € (0; 1,5)
 алее мы можем составить систему уравненй, выражая а через х:
алее мы можем составить систему уравненй, выражая а через х: х2-а2=0 9х2=а2 а=± 3а
х2-а2=0 9х2=а2 а=± 3а 
 алее решаем систему уравнений: где оба уравнения линейные
алее решаем систему уравнений: где оба уравнения линейные


 еперь поняв какие варианты возможны, приступаем к решению задачи. Условия задачи: образуют отрезок длинны 1 означает х2-х1=1. Запишем 2 сисемы уравнений удовлетворяющих условию:
еперь поняв какие варианты возможны, приступаем к решению задачи. Условия задачи: образуют отрезок длинны 1 означает х2-х1=1. Запишем 2 сисемы уравнений удовлетворяющих условию: 2-х1=1 х2-х1=1 х2-х1=1 х2=-1,5 а1=-2,5
2-х1=1 х2-х1=1 х2-х1=1 х2=-1,5 а1=-2,5
 х2-х1=1 х2-х1=1 х2-х1=1 х1=-4,5 а2=-9,5
х2-х1=1 х2-х1=1 х2-х1=1 х1=-4,5 а2=-9,5 2=32 (│х│-1)2, такое возможно только в двух случаях:
2=32 (│х│-1)2, такое возможно только в двух случаях:

 твет: а € (-∞;3) ⋃ 0 ⋃ (3; ∞)
твет: а € (-∞;3) ⋃ 0 ⋃ (3; ∞)










