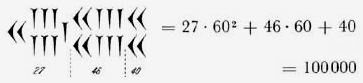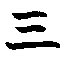Муниципальное общеобразовательное учреждение
Гимназия №11 Дзержинского района Города Волгограда
Районная учебно-исследовательская конференция для учащихся 5-8 классов
«На пути открытий» секция математика
Нумерация у разных народов
Выполнила:
Мухортов Артем Сергеевич
ученик 5 В класса
Учитель:
Булгакова Елена Юрьевна
Волгоград 2016
СОДЕРЖАНИЕ:
Введение……………………………………………………………………2
Основная часть…………………………………………………………….4
Понятие нумерации……………………………………………………4
История возникновения нумерации………………………………….4
Виды нумераций……………………………………………………….5
Словесная нумерация………………………………………………….5
Египетская нумерация…………………………………………………6
Вавилонская нумерация……………………………………………….8
Греческая нумерация…………………………………………………..9
Римская нумерация……………………………………………………10
Славянская Кириллическая нумерация………………………………11
Славянская глаголическая нумерация………………………………..12
Китайская нумерация………………………………………………….14
Нумерация индейцев Майя……………………………………….......16
Арабская нумерация………………………………………………..18
Практическая часть……………………………………………………….19
Заключение ……………………………………………………………….20
Используемая литература………………………………………………..21
ВВЕДЕНИЕ
Изучая математику как науку, мы иногда забывает о самых истоках развития этого направления человеческого мышления. Почему у разных народов различные способы подсчета, влияет ли это на развитие практической математики, поэтому исследование способов счета, то есть систем счисления, является актуальной темой. Как человек начал считать? Почему цифры, которые мы пишем каждый день, имеют именно такой вид, а не другой? Почему одни считают десятками, а другие дюжинами? И, в конечном счете, почему разные народы сформировали разные способы подсчета или иначе – системы счисления?
Перед началом исследования была сформулирована гипотеза исследования:
Десятичная система счисления является наиболее применяемой среди всего многообразия систем счисления, так как обеспечивает наиболее простой и удобный счет.
Цель исследования:
Выявить из всего разнообразия систем счисления наиболее удобный способ записи чисел.
Поставленная цель потребовала решения следующих задач:
рассмотреть понятие системы счисления, нумерации;
рассмотреть историю возникновения систем счисления с различными основаниями;
познакомиться с существующими системами счисления;
выявить достоинства и недостатки систем счисления с различными основаниями.
Теоретической и информационной основой исследования являются работы отечественных и зарубежных авторов по истории возникновения систем счисления, по теории систем счисления, такие как Лейбниц, Балобанов.
Объект исследования:
Запись цифр у разных народов.
Предмет исследования: нумерология.
Сохранилась гравюра 1512 года (рис. 9), на которой изображены три персонажа: по центру богиня-аллегория Арифметика, справа от нее сидит новатор Боэций, делающий записи арабскими цифрами, а слева — консерватор Пифагор, считающий на абаке (сбоку на лентах написаны их имена). Богиня Арифметика явно благоволит Боэцию, у нее на платье видны арабские числа.

Гравюра Грегори Райша (Gregor Reisch) 1512 года, Страсбург.
ОСНОВНАЯ ЧАСТЬ.
1. Понятие нумерации.
В чем разница нумерации и системы счисления?
Нумерация (нумерация лат. numeratio) – метод обозначения чисел с помощью знаков – цифр или слов. Система обозначения, основанная на цифрах – это письменная нумерация. Система обозначения, основанная на словах – это словесная нумерация;
Система счисления – очень сложное понятие. Оно включает в себя все законы, по которым числа записываются и читаются, а так же те, по которым производятся операции над ними;
Несмотря это нумерация и система счисления тесно переплетаются, предназначены для того, чтобы человек имел возможность записать или произнести любое число.
Любая система счисления имеет так называемое основание, которое, как правило, звучит уже в самом названии системы счисления, например, десятичная, двоичная или двенадцатеричная. Определить основание очень легко, нужно только пересчитать количество значащих цифр в системе. Мы, например, используем цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Их ровно 10, поэтому основание нашей системы счисления тоже 10, и система счисления называется «десятичная».
2. История возникновения нумерации.
«Если бы число пальцев на руках и ногах у человека было другое, иные были бы, конечно, господствующие во всем мире системы счисления; расти на руках у человека еще по одному пальцу, цивилизованные народы приняли бы за основание счета не десяток, а дюжину.» Ф. Кэджори
Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления. В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит (нумерация).
Примеры позиционных систем счисления: десятичная система счисления, основанная на арабских цифрах; древневавилонянская (60-ричная); система Майя (20-ричная).
Примеры непозиционных систем счисления — римская, старая и новая греческая, славянская.
В большинстве стран мира, несмотря на то, что там говорят на разных языках, считают одинаково, «по-арабски». Но так было не всегда. Еще каких-то пятьсот лет назад ничего подобного и в помине не было даже в просвещенной Европе. Но тем не менее числа люди все равно как-то записывали.
У каждого народа была своя собственная или позаимствованная у соседа система записи чисел. Одни использовали буковки, другие - значки, третьи - закорючки. У кого-то получалось удобнее, у кого-то не очень.
Навязывание узелков Зарубки на дереве Нанизывание ракушек.
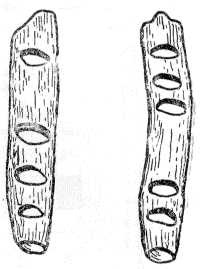

3. Виды нумераций.
1) Словесная нумерация
Люди начали считать с того самого отдаленного времени, когда стали группироваться в общества. Счет был нужен хотя бы для того, чтобы знать количество членов семьи или размер стада.
Первобытному человеку не сразу понадобились слова для обозначения чисел. Ученые считают, что изначально первобытные люди знали только «один», «два» и «много». Это подтверждается тем, что в некоторых языках, например в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа.
Поэтому первыми словами, которые человек стал использовать для обозначения небольших чисел стали имена предметов, всегда встречающихся человеку в соответствующем количестве. Например, известно, что в Индии ноль обозначался словами «пустое», «небо», «дыра»; единица - предметами, имеющимися только в единственном числе: Луна, Земля; двойка - словами «близнецы», «глаза», «ноздри», «губы»; четверка - словами «океаны», «стороны света».
Еще в V в. В Индии встречается запись числа 1021 словами «Луна - дыра - крылья - Луна».
словесная система счисления предполагает отдельные слова для обозначения чисел первого порядка.
В русском языке таких слов десять: один, два, три, четыре, пять, шесть, семь, восемь, девять, десять.
В английском языке таких слов 12: one, two, three, four, five, six, seven, eight, nine, ten, eleven, twelve.
Для того, чтобы образовать слова второго порядка в русском языке используется суффикс –надцать. Для образования десятков в русском языке служат суффиксы - -дцать и –десять. Для образования сотен в русском языке используются суффиксы - -ста, -сот.
2) Египетская нумерология.
Египтяне придумали эту систему около 5 000 лет тому назад. Это одна из древнейших систем записи чисел, известная человеку.
Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
Так, для обозначения, например, числа 3815, рисовали три цветка лотоса, восемь пальмовых листов, одну дугу и пять шестов.
Иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах.
|
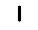
| 1. Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки. |
|
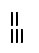
| Если палочек нужно изобразить несколько, то их изображали в два ряда, причем в нижнем должно быть столько же палочек сколько и в верхнем, или на одну больше. |
|
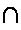
| 10. Такими путами египтяне связывали коров |
|
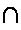 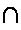 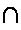
| Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. |
|
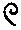
| 100. Это мерная веревка, которой измеряли земельные участки после разлива Нила. |
|
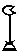
| 1 000. Вы когда-нибудь видели цветущий лотос? Если нет, то вам никогда не понять, почему Египтяне присвоили такое значение изображению этого цветка. |
|
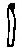
| 10 000. "В больших числах будь внимателен!" - говорит поднятый вверх указательный палец. |
|

| 100 000. Это головастик. Обычный лягушачий головастик. |
|
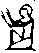
| 1 000 000. Увидев такое число обычный человек очень удивится и возденет руки к небу. Это и изображает этот иероглиф |
|
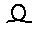
| 10 000 000. Египтяне поклонялись Амону Ра, богу Солнца, и, наверное, поэтому самое большое свое число они изобразили в виде восходящего солнца. |
Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то переходили к следующему разряду.
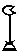
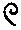
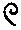
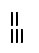 - 1207,
- 1207, 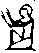
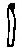
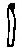
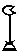
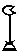
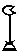
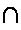
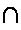
 - 1 023 029
- 1 023 029
3) Вавилонская нумерология. (шестидесятеричная система)
Также далеко от наших дней, за две тысячи лет до н.э., в другой великой цивилизации — вавилонской — люди записывали цифры по-другому. Вавилоняне делали записи острой палочкой на мягких глиняных табличках, которые затем обжигались на солнце или в печи. Эти записи оказались исключительно долговечными, в музеях мира хранятся десятки тысяч клинописных табличек.
Числа менее 60 обозначались с помощью двух знаков: 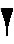 для единицы, и
для единицы, и 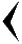 для десятка. Они имели клинообразный вид. Эти знаки повторялись нужное число раз, например
для десятка. Они имели клинообразный вид. Эти знаки повторялись нужное число раз, например
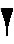
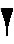
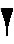 - 3;
- 3; 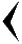
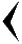 - 20;
- 20; 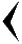
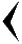
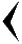
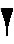
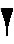 - 32
- 32
Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую.. Принцип повторного использования знаков позволял, например, записать число 59 в виде , т.е. 5*10 + 9
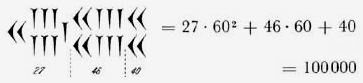
В целом шестидесятиричная система счисления громоздка и неудобна.
Система вавилонян сыграла большую роль в развитии математики и астрономии, ее следы сохранились и до наших дней. Так, мы до сих пор делим час на 60 минут, а минуты на 60 секунд. Следуя примеру вавилонян, мы и окружность делим на 360 частей (градусов).
4) Греческая нумерология.
В Древней Греции имели хождение две основных системы счисления - аттическая (или геродианова) и ионическая (она же александрийская или алфавитная). Аттическая система счисления использовалась греками, по-видимому, уже к 5 в. до н.э.
По существу это была десятичная система (хотя в ней также было выделено и число пять), а аттические обозначения чисел использовали повторы коллективных символов. Черта, обозначавшая единицу, повторенная нужное число раз, означала числа до четырех. После четырех черт греки вместо пяти черт ввели новый символ Г, первую букву слова «пента» (пять) (буква Г употреблялась для обозначения звука «п», а не «г»). Дойдя до десяти, они ввели еще один новый символ, первую букву слова «дека» (десять).
Так как система была десятичной, грекам потребовались новые символы для каждой новой степени числа 10: символ H означал 100 (гекатон), X - 1000 (хилиои), символ M - 10000 (мириои или мириада).
Чтобы отличить числа от слов, греки над соответствующей буквой ставили горизонтальную черту. Первоначально числа обозначались прописными буквами, но позднее сменились на строчные.
5) Римская нумерология
Римские обозначения чисел известны ныне лучше, чем любая другая древняя система счисления. С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д. Объясняется это не столько какими-то особыми достоинствами римской системы, сколько тем огромным влиянием, которым пользовалась Римская империя в сравнительно недавнем прошлом.
Знакомая нам римская система не слишком принципиально отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно, являющиеся цифрами этой системы счисления.
I V X L C D M
1 5 10 50 100 500 1000
Число в римской системе счисления обозначается набором стоящих подряд цифр. Значение числа равно:
1) сумме значений идущих подряд нескольких одинаковых цифр (назовем их группой первого вида);
2) разности значений двух цифр, если слева от большей цифры стоит меньшая. В этом случае от значения большей цифры отнимается значение меньшей цифры. Вместе они образуют группу второго вида. Заметим, что левая цифра может быть меньше правой максимум на один порядок: так, перед L (50) и C (100) из «младших» может стоять только X (10), перед D (500) и M(1000) — только C (100), перед V (5) — только I (1);
3) сумме значений групп и цифр, не вошедших в группы первого или второго вида.
Например, IX обозначает 9, XI обозначает11. Десятичное число 28 представляется следующим оброзом: XXVIII=10+10+5+1+1+1, а десятичное число 99 имеет вот такое представление: IC= -1+100.
Хотя о первоначальном значении этих символов было написано много, их удовлетворительного объяснения у нас нет до сих пор. Согласно одной из распространенных теорий, римская цифра V изображает раскрытую руку с четырьмя прижатыми друг к другу пальцами и отставленным большим пальцем; символ X, согласно той же теории, изображает две скрещенные руки или сдвоенную цифру V.
6) Славянская кириллическая нумерация
Эта нумерация была создана вместе со славянской алфавитной системой для переписки священных книг для славян греческими монахами братьями Кириллом (Константином) и Мефодием в IX веке. Эта форма записи чисел получила большое распространение в связи с тем, что имела полное сходство с греческой записью чисел. Если посмотреть внимательно, то увидим, что после «а» идет буква «в», а не «б» как следует по славянскому алфавиту, то есть используются только буквы, которые есть в греческом алфавите. До XVII века эта форма записи чиcел была официальной на территории современной России, В России славянская нумерация сохранилась до конца XVII в. При Петре I возобладала так называемая арабская нумерация, которой мы пользуемся и сейчас. Славянская нумерация сохранилась только в богослужебных книгах.
До сих пор православные церковные книги используют эту нумерацию.
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали. Интереснее всего записывались числа второго десятка.
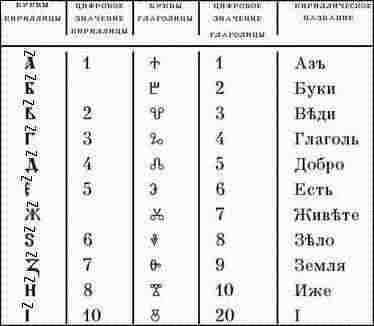
Читаем дословно «четырнадцать» - «четыре на десять». Как слышим, так и пишем: не 10+4, а 4+10, - четыре на десять. И так для всех чисел от 11 до 19. Таким образом у славян мы прослеживаем десятеричную систему счисления.
В России славянская нумерация сохранилась до конца XVII века. В начале 17-го века новая нумерация проникает в Россию, но православная церковь встречает ее в штыки и объявляет новую нумерацию колдовской и безбожной. Закрепилась десятичная нумерация в России только после издания в 1703 году знаменитой «Арифметики» Магницкого, в которой все вычисления в тексте производились исключительно с использованием десятичной системы счисления.
7) Славянская глаголическая нумерация
Эта нумерация была создана для переписки чисел в священных книгах западных славян. Использовалась она нечасто, но достаточно долго. По организации она в точности повторяет греческую нумерацию. Использовалась она с VIII по XIII в.
|
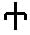 1 1
|
 10 10
|
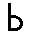 100 100
|
 1 000 1 000
|
|
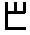 2 2
|
 20 20
|
 200 200
|
|
|
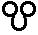 3 3
|
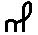 30 30
|
 300 300
|
|
|
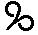 4 4
|
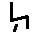 40 40
|
 400 400
|
|
|
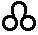 5 5
|
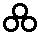 50 50
|
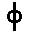 500 500
|
|
|
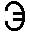 6 6
|
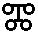 60 60
|
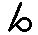 600 600
|
|
|
 7 7
|
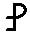 70 70
|
 700 700
|
|
|
 8 8
|
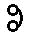 80 80
|
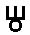 800 800
|
|
|
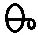 9 9
|
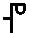 90 90
|
 900 900
|
|
Записывались цифры числа начиная с больших значений и заканчивая меньшими, слева направо. Если десятков, единиц, или какого-то другого разряда не было, то его пропускали
Такая запись числа аддитивная, то есть в ней используется только сложение:
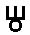
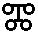
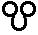 = 800+60+3 = 863
= 800+60+3 = 863
8) Китайская нумерация
Эта нумерация одна из старейших и самых прогрессивных, поскольку в нее заложены такие же принципы, как и в современную арабскую, которой мы пользуемся. Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.
Эта система возникла как результат оперирования с палочками, выкладываемыми для счета на стол или доску. Числа от единицы до пяти обозначались, соответственно, одной, двумя и т.д. палочками, выкладываемыми вертикально, а одна, две, три или четыре вертикальные палочки, над которыми помещалась одна поперечная палочка, означали числа шесть, семь, восемь и девять.
Первые пять кратных числа 10 обозначались одной, двумя, пятью горизонтальными палочками, а одна, две, три и четыре горизонтальные палочки, к которым сверху приставлялась вертикальная палочка, означали числа 60, 70, 80 и 90. Для обозначения чисел больше 99 использовался позиционный принцип.
Обозначения чисел с помощью палочек тесно связано со счетом на пальцах и счетной доске, но применялось оно также и в письменных вычислениях. Во второй китайской системе счисления для обозначения первых девяти целых чисел или символов используют девять различных знаков и одиннадцать дополнительных символов для обозначения первых одиннадцати степеней числа 10. В сочетании с умножением и вычитанием это позволяло записывать любое число меньше триллиона. Если один из символов, обозначающих первые девять целых чисел, стоит перед (при чтении слева направо) символом, означающим степень числа 10, то первое нужно умножить на второе, если же символ одного из девяти первых целых чисел стоит на последнем месте, то это число надлежит прибавить к обозначенному предыдущими символами.
Возникла эта нумерация около 4 000 тысяч лет тому назад в Китае.

 - 1 000;
- 1 000; 



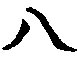 - 548
- 548
Записывались цифры числа начиная с больших значений и заканчивая меньшими. Если десятков, единиц, или какого-то другого разряда не было, то сначала ничего не ставили и переходили к следующему разряду
В 17 в. вошла в употребление десятичная запятая (или точка), которой стали отделять целую часть числа от дробной. После этих изменений развитие современной системы счисления завершилось. Это отнюдь не означает, будто была достигнута полная стандартизация в названиях или обозначениях чисел. В Америке и Франции биллион означает тысячу миллионов, а в Англии и Германии - миллион миллионов; в континентальной Европе часто используется десятичная запятая, а в англосаксонских странах предпочитают ставить десятичную точку; англосаксы используют запятые, чтобы отделять степени тысячи, в некоторых странах для этой цели служит точка.
9) Нумерация индейцев Майя
Эта нумерация очень интересна тем, что на ее развитие не повлияла ни одна из цивилизаций Старого Света. Однако в ней использованы все те же принципы. Сначала эта нумерация обслуживала пятиричную систему счисления, а потом ее приспособили для двадцатиричной.
|

|
1
|

|
9
|
|

|
2
|

|
10
|
|

|
3
|

|
11
|
|

|
4
|

|
12
|
|

|
5
|

|
13
|
|

|
6
|

|
15
|
|

|
7
|

|
19
|
|

|
8
|

|
0 или 20
|
Записывались цифры числа в столбик, начиная со знаков  , затем знаки
, затем знаки  , а потом
, а потом  больших значений и заканчивая меньшими.
больших значений и заканчивая меньшими.
10) Арабская нумерация.
Способ записи чисел, при котором один и тот же знак (цифра) из десяти: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 имеет различные значения в зависимости от того места, где он расположен. Десять единиц 1-го разряда (места, занимаемого в числе) образуют единицу следующего разряда - число 10, десять единиц 2-го разряда образуют единицу 3-го разряда - число 100 и т.д. Например, 362=3*100+6*10+2. числа от 11 (один — на десять) до 19 (девять —I на десять) записывали так же, как говорили, то есть «цифру» единиц ставили до «цифры» десятков. Для того, чтобы образовать слова второго порядка – восемь+десять. Для образования сотен -, - пять+сот.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Запись даты моего дня рождения в различной нумерологии.
Моя дата.30.03.2004.
1)Египетские
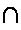
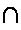
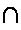
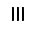
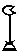
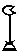
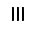
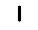
2)Греческие
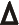
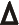
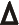
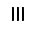 XX
XX 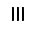
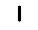
3)Римские
ХХХ III ММ IV
4) Китайские



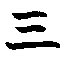



Запишем интересные факты Волгограда в разных системах счисления.
1) Длина г. Волгограда-95км (египетская нумерология)
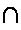
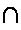
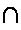
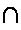
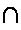
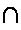
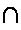
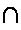
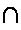
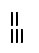
2) Длина 3-й Продольной-40км (римская нумерология)
XL
3) Высота монумента Родина-Мать-85м (греческая нумерология)
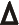
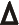
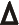
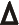
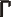
4) Самый длинный дом-1125м (китайская нумерология)





5) Длина моста через р. Волгу-7100м (славянская нумерология)







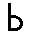
6) Длина моста через р. Ахтуба-6500м (греческая нумерология)
XXXXXXHHHHH
7)Возраст г. Волгограда-427лет (египская нумерология)
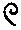
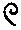
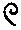
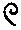
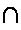
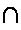
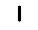
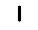
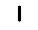
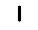
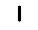
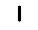
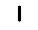
8) Длина Волго-Донского канала-101км (китайская нумерология)


9) Длина Волжской ГЭС-4100м (славянская нумерология)




ЗАКЛЮЧЕНИЕ.
Познакомившись с различной литературой по интересующей меня теме, я понял, что развитие числа и системы счисления было долгим и трудным, нумерология претерпела множество изменений по мере развития и становления человеческого общества, при плавном переходе от древнего человека к современной личности
Отголоски использования различных древних систем счета нашли отражение в современном мире.
Изучив различные виды нумераций и применив на практике пришел к выводу: наиболее удобная арабская система счисления, которой мы пользуемся по настоящее время.
Используемая литература.
С. Б. Гашков Системы счисления и их применение. — М.: МЦНМО, 2004. — (Библиотека «Математическое просвещение»).
Депман И.Я. Виленкин Н.Я За страницами учебника математики. Пособие для учащихся 5-6 классов средней школы М.»Просвещение» 1989г.287стр.
"Российское предпринимательство" Журнал по экономике. Статья Кузьмищева В.А «О системах счисления»
С. В. Фомин Системы счисления. — М.: Наука, 1987. — 48 с. — (Популярные лекции по математике). Шестаков А.П. Введение в информатику. Пермский университет. Пермь. 1999
Яглом И., «Системы счисления», Квант, № 6, 1970.
www.creativeconomy.ru В. А. Кузьмищев Тайна жрецов майя
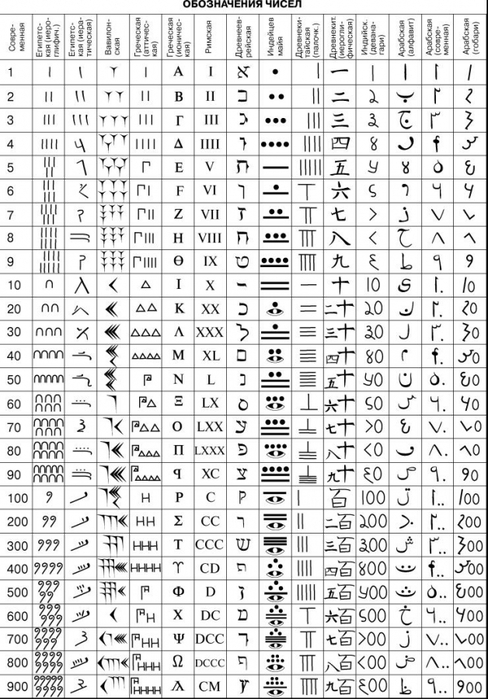
Приложение.
28