Вариант 1.
Модуль «Алгебра»
1. Найдите значение выражения 
2. Одна из точек, отмеченных на координатной прямой, соответствует числу  .Какая это точка?
.Какая это точка?
1) точка A
2) точка B
3) точка C
4) точка D
3. Сравните числа  и 16.
и 16.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4. Решите уравнение: 
5. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 
Б) 
B) 
ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
6. Дан числовой набор. Его первое число равно 6,2, а каждое следующее число на 0,6 больше предыдущего. Найдите пятое число этого набора.
7. Упростите выражение  и найдите его значение при
и найдите его значение при  . В ответе запишите найденное значение.
. В ответе запишите найденное значение.
8. Решите систему уравнений: 
Модуль «Геометрия»
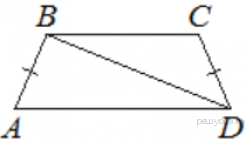
9. В трапеции  известно, что
известно, что  ,
,  и
и  . Найдите угол
. Найдите угол  . Ответ дайте в градусах.
. Ответ дайте в градусах.

10. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB Найдите угол ACB, если угол AOB равен 47°. Ответ дайте в градусах
11. Основания трапеции равны 18 и 12, одна из боковых сторон равна  , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
12. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.
13. Какое из следующих утверждений верно?
1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Сумма углов прямоугольного треугольника равна 90 градусам.
3) Биссектрисы треугольника пересекаются в центре вписанной в него окружности.
Модуль « Реальная Математика»
14. В таблице представлены налоговые ставки на автомобили в Москве с 1 января 2013 года.
| Мощность автомобиля (в л. с.) | Налоговая ставка (в руб. за л. с. в год) |
| не более 70 | 0 |
| 71—100 | 12 |
| 101—125 | 25 |
| 126—150 | 35 |
| 151—175 | 45 |
| 176—200 | 50 |
| 201—225 | 65 |
| 226—250 | 75 |
| свыше 250 | 150 |
Сколько рублей должен заплатить владелец автомобиля мощностью 219 л. с. в качестве налога за один год?
В ответе укажите номер правильного варианта.
1) 14 235
2) 75
3) 65
4) 16 425
15. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в километрах) давление составит 540 миллиметров ртутного столба?

16.В начале учебного года в школе было 1250 учащихся, а к концу года их стало 950. На сколько процентов уменьшилось за год число учащихся?
17. Картинка имеет форму прямоугольника со сторонами 12 см и 32 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 684 см. Какова ширина окантовки? Ответ дайте в сантиметрах.
18. На диаграмме показано содержание питательных веществ в какао, молочном шоколаде, фасоли и сливочных сухарях. Определите по диаграмме, в каком продукте содержание углеводов наименьшее.
1) какао
2) шоколад
3) фасоль
4) сухари
19. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?
20. Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле где  — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
— длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.
Вариант 2.
Модуль «Алгебра»
1. Найдите значение выражения
2. Какое из следующих чисел заключено между числами  и
и 
В ответе укажите номер правильного варианта.
1) 0,4
2) 0,5
3) 0,6
4) 0,7
3. Представьте выражение в виде степени с основанием x.
1) x−5
2) x5
3) x50
4) x−50
4. Найдите корни уравнения
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. На рисунке изображены графики вида Установите соответствие между графиками функций и знаками коэффициентов k и b.
Графики
Коэффициенты
| 1) k b 0 | 2) k 0, b 0 | 3) k b |
Ответ:
6. Какое наименьшее число последовательных натуральных чисел, начиная с 1, нужно сложить, чтобы получившаяся сумма была больше 465?
7. Найдите значение выражения при
8. Решите систему уравнений:
Модуль « Геометрия»
9. Площадь равнобедренного треугольника равна Угол, лежащий напротив основания равен 120°. Найдите длину боковой стороны.
10. Найдите ∠KOM, если градусные меры дуг KO и OM равны 112° и 170° соответственно.
11. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника.
12. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите длину её средней линии.
13. Какое из следующих утверждений верно?
1. Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.
2. Тангенс любого острого угла меньше единицы.
3. Сумма углов равнобедренного треугольника равна 180 градусам.
Модуль « Реальная математика»
14. В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
| Мальчики | Девочки |
| Отметка | «5» | «4» | «3» | «5» | «4» | «3» |
| Время, секунды | 4,6 | 4,9 | 5,3 | 5,0 | 5,5 | 5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,92 секунды?
В ответе укажите номер правильного варианта.
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
15. В таблице приведена стоимость работ по покраске потолков.
| Цвет потолка | Цена в рублях за 1 м2 (в зависимости от площади помещения) |
| до 10 м2 | от 11 до 30 м2 | от 31 до 60 м2 | свыше 60 м2 |
| белый | 105 | 85 | 70 | 60 |
| цветной | 120 | 100 | 90 | 85 |
Пользуясь данными, представленными в таблице, определите, какова будет стоимость работ, если площадь потолка 40 м2, потолок цветной и действует сезонная скидка в 10%. Ответ укажите в рублях.
16. Во время выборов голоса избирателей между двумя кандидатами распределились в отношении 2:3. Сколько процентов голосов было отдано за победителя?
17. Лестницу длиной 2 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,2 м?
18. На диаграмме показан религиозный состав населения Германии. Определите по диаграмме, в каких пределах находится доля католиков.
1) 0−10%
2) 10−15%
3) 15−25%
4) 25−45%
19. В фирме такси в данный момент свободно 20 машин: 9 черных, 4 желтых и 7 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
20. Закон Кулона можно записать в виде где  — сила взаимодействия зарядов (в ньютонах),
— сила взаимодействия зарядов (в ньютонах),  и
и  — величины зарядов (в кулонах),
— величины зарядов (в кулонах),  — коэффициент пропорциональности (в Н·м2/Кл2 ), а
— коэффициент пропорциональности (в Н·м2/Кл2 ), а  — расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда
— расстояние между зарядами (в метрах). Пользуясь формулой, найдите величину заряда  (в кулонах), если Н·м2/Кл2, Кл, м, а
(в кулонах), если Н·м2/Кл2, Кл, м, а  Н.
Н.
Вариант 3.
Модуль «Алгебра»
1. Найдите значение выражения
2. На координатной прямой точками отмечены числа  ; 0,42; 0,45. Какому числу соответсвует точка B?
; 0,42; 0,45. Какому числу соответсвует точка B?
В ответе укажите номер правильного варианта.

1)  2)
2)  3) 0,42 4) 0,45
3) 0,42 4) 0,45
3. Площадь территории Китая составляет 9,6 млн км2. Как эта величина записывается в стандартном виде?
1) 9,6*105 км2
2) 9,6*106 км2
3) 9,6*10 7 км2
4) 9,6*108 км2
4. Решите уравнение −2(5 − 3x) = 7x + 3.
5. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) 
Б) 
B) 
ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
6. Последовательность задана формулой  . Сколько членов в этой последовательности больше 1?
. Сколько членов в этой последовательности больше 1?
7. Найдите значение выражения при a = 78, c = 21.
8. Решите систему уравнений:
Модуль «Геометрия»
9. В равнобедренном треугольнике . Найдите  , если высота .
, если высота .
10. Найдите площадь квадрата, описанного вокруг окружности радиуса 39.
11. Основания трапеции равны 2 и 18, одна из боковых сторон равна , а угол между ней и одним из оснований равен 120°. Найдите площадь трапеции.
12. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
13. Какое из следующих утверждений верно?
1) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
2) В параллелограмме есть два равных угла.
3) Площадь прямоугольного треугольника равна произведению длин его катетов.
Если утверждений несколько, запишите их номера в порядке возрастания.
Модуль «Реальная математика»
14. В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из этих планет дальше всех от Солнца?
| Планета | Меркурий | Уран | Марс | Сатурн |
| Расстояние (в км) | 5,79 · 107 | 2,871 · 109 | 2,28 · 108 | 1,427 · 109 |
1) Меркурий
2) Уран
3) Марс
4) Сатурн
15. На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах).На сколько миллиметров ртутного столбы отличается давление на высоте 2 км от давления на высоте 8 км?
16. Брюки дороже рубашки на 20%, а пиджак дороже рубашки на 44%. На сколько процентов пиджак дороже брюк?
17. Какой угол (в градусах) образуют минутная и часовая стрелки, когда часы показывают ровно 4 часа?
18. В доме располагаются однокомнатные, двухкомнатные, трёхкомнатные и четырёхкомнатные квартиры. Данные о количестве квартир представлены на круговой диаграмме.
Какие из утверждений относительно квартир в этом доме неверны, если всего в доме 180 квартир?
1) Больше половины квартир двухкомнатные.
2) Однокомнатных квартир менее четверти.
3) Четверть всех квартир — трёхкомнатные.
4) Однокомнатных, двухкомнатных и трёхкомнатных
квартир всего более 165.
В ответе запишите номера выбранных утверждений.
19. На экзамене 50 билетов, Руслан не выучил 5 из них. Найдите вероятность того, что ему попадется выученный билет.
20. Чтобы перевести значение температуры по шкале Цельсия (t °C) в шкалу Фаренгейта (t °F), пользуются формулой F = 1,8C + 32 , где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 6° по шкале Фаренгейта? Ответ округлите до десятых.








 .Какая это точка?
.Какая это точка?
















