Итоговое повторение в 9 классе : Теорема Пифагора и подобные треугольники

Урок-тренинг по геометрии в 9 классе

«Решение планиметрических задач по темам «Теорема Пифагора» и «Подобие треугольников» из открытого банка заданий ОГЭ »

Цели и задачи урока:

Образовательная: Систематизировать знания учащихся по ключевым разделам планиметрии. Создать содержательные и организационные условия для применения школьниками комплекса знаний для решения задач, включаемых в материалы ГИА.

Развивающая: Развивать личностно-смысловые отношения учащихся к изучаемому предмету. Способствовать формированию коллективной и самостоятельной работы, формировать умение четко и ясно излагать свои мысли.

Воспитательная: Развитие памяти, внимания, логического мышления, наблюдательности. Развитие способности обобщать, классифицировать. Развитие самоконтроля. Воспитание настойчивости в достижении цели и заинтересованности в конечном результате труда.

Тип урока: повторения, обобщения и систематизации знаний.

Технологии: ИКТ - технология, дифференцированного обучения.

Оборудование: проектор, экран, компьютер, ноутбуки, презентация Power Point, карточки с заданиями, карточки с опорным конспектом, листы самооценки , таблица квадратов двузначных чисел .

Структура урока:

1. Организационный момент.

2. Актуализация опорных знаний:
   1 ) математический диктант ;
   2) повторение теоретического материала;
   3) устное решение задач; 4) письменное решение задач;

3. Обобщающая деятельность учащихся( итоговый тест)

4. Итог урока.

«Легко в учении – тяжело в походе, тяжело в учении – легко в походе. Тяжело в учении – легко в бою»
А.В. Суворов.

ХОД УРОКА.

1. Организационный момент

Слайд 1 Здравствуйте дорогие ребята и уважаемые коллеги. Не случайно эпиграфом сегодняшнего урока служат одна из любимых фраз великого русского полководца , генералиссимуса А.В. Суворова. Ведь учение помогает довести навыки до автоматизма. Это касается любой профессиональной деятельности. И нам, чтобы успешно сдать экзамены нужно много тренироваться. Мы с вами не можем знать заранее, какие задачи будут на экзамене. Поэтому, чтобы уверенно решать предложенные задачи, надо хорошо знать теорию, т.е. определения и формулировки теорем. Иногда из-за одного пропущенного слова меняется смысл сказанного. Вы знаете, чтобы успешно сдать экзамен по математике , нужно верно решить 2 задания из модуля «Геометрия».

Слайд 2 И чаще всего в этих заданиях встречается темы «Теорема Пифагора» и «Подобные треугольников». Причём явно и неявно. Поэтому мы начнём наш тренировку с проверки знания теории.

1. Актуализация опорных знаний

И начнём мы с математического диктанта . Слушайте внимательно

1. Математический диктант

1. Закончите предложение: Два треугольника  называются подобными, если их углы соответственно равны и стороны одного треугольника …

2. Закончите предложение:  Отношение площадей двух подобных треугольников равно…

3. Подобны ли треугольники, если два угла одного треугольника равны двум углам другого?

4. Подобны ли два равносторонних треугольника ?

5. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов?

Слайд 3 Ребята , сравните ваши ответы . За каждый правильный ответ 1 балл. Занесите ваш результат в лист успеха.

1. Повторение теоретического материала

Слайд 4. Поднимите руки те, кто верно ответил на последний вопрос? Что это за утверждение? Теорема Пифагора

Ещё раз, для каких треугольников она справедлива? Для прямоугольных

Как называются стороны прямоугольного треугольника? Катеты и гипотенуза

Слайд 5. А теперь обратимся к сайту «Распечатай и реши». В задании 15 представлены несколько типов задач на применение теоремы Пифагора. Давайте посмотрим, сколько их? В каких задачах применение теорема Пифагора видно сразу ( в трёх верхних) , а в каких она «спрятана» ( в трёх нижних) ?

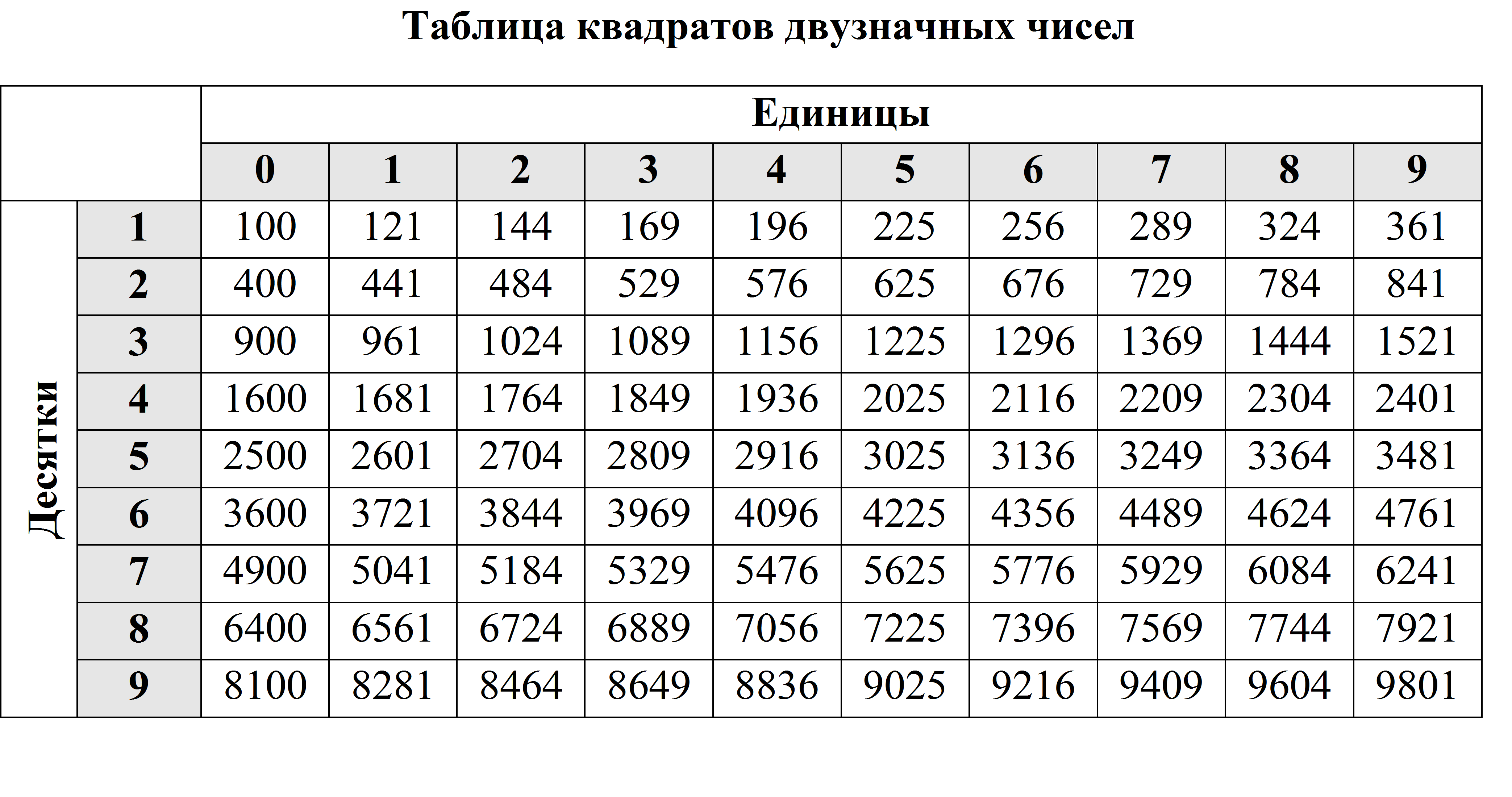
Слайд 6. Основные задачи. Попробуйте выполнить самостоятельно задачи 1-3. Для выполнения данного задания нам понадобится таблица квадратов двухзначных чисел( ПРИЛОЖЕНИЕ 3)

Ребята, сравните ваши ответы с верными. За каждый правильный ответ по 1 баллу . Общее количество поставьте в лист самооценки . ( ПРИЛОЖЕНИЕ 4) Все задачи получились? Проговариваем их устно.

А теперь на листах с классной работой ( ПРИЛОЖЕНИЕ 1) записываем сегодняшнее число. Лист с классной работой у вас на столе. Записываем число и выполняем дополнительные построения и записи прямо на листе. И на трёх оставшихся задачах остановимся поподробнее.

Слайд 7. № 1 От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на вы­соте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м. Ответ дайте в метрах.

Ученик у доски. Решает самостоятельно или по наводящим вопросам

С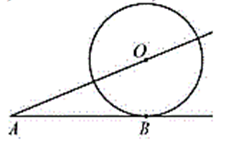 лайд 8 № 2 Найти радиус окружности, если АВ = 12см, ОА = 13см.

Ученик у доски. Решает самостоятельно или по наводящим вопросам

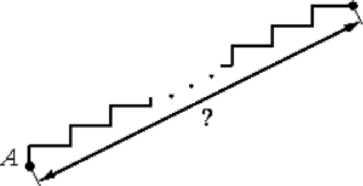
Слайд 9 № 3 Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина - 96 см. Найдите расстояние ме­жду точками A и B (в метрах).

Весь класс в тетради . Решает вместе с учителем по наводящим вопросам

Рефлексия по Теореме Пифагора Решение скольких задач мы повторили? Если остались вопросы, то мы их разберём на групповом занятии индивидуально

Слайд 9 А теперь поговорим о подобных треугольниках. Дайте, пожалуйста, определение подобных треугольников.

Слайд 10 Сначала вспомним , как называются стороны в треугольниках, если углы одного равны углам другого .

Слайд 11 Сходственные

Слайд 12 А теперь дайте определение подобных треугольников.

Слайд 13. Какое число называется коэффициентом подобия? Сколько признаков подобия вам известно? Формулировки признаков подобия . Ребята, если мы находим отношение меньшего треугольника к большему, то число k больше или меньше единицы? А если наоборот?

Слайды 14 – 16 Устно Задачи на определение коэффициента подобия и неизвестных сторон ( блиц - опрос)

Слайды 17- 19 Устно Формулировка признаков подобия

Слайд 20 И снова обратимся к типовым задачам на подобные треугольники.

Давайте разберём их все вместе. Таблица с теорией по подобным треугольникам у вас на столе. ( ПРИЛОЖЕНИЕ 2)

Слайд 21 Кто знает, как выполняются задания, то решает самостоятельно, а у кого есть вопросы мы их вместе разберём.

С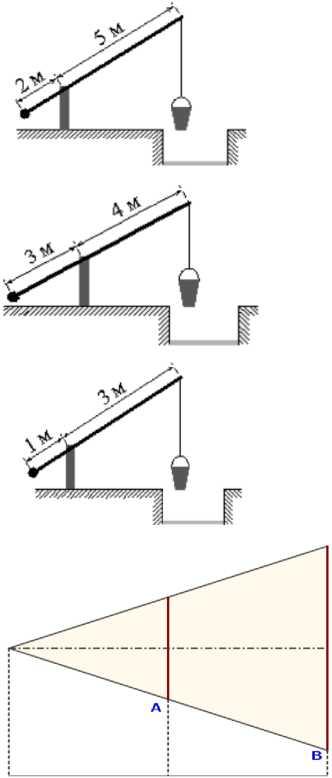 лайд 22 № 4 На рисунке изображён колодец с «журавлём». Корот­кое плечо имеет длину 2 м, а длинное плечо - 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?

С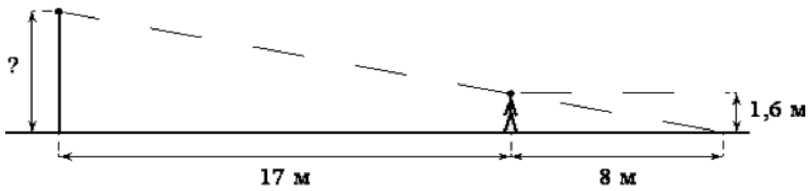 лайд 23 № 5 Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря

С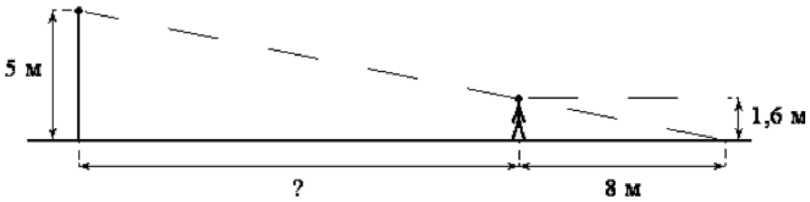 лайд 24 № 6 На каком рас­стоянии (в метрах) от фонаря стоит че­ловек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?

С лайд 25 № 7 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в см) от проектора нужно расположить экран B вы­сотой 320 см, чтобы он был полностью освещён, ес­ли настройки проектора остаются неизменными?

Слайд 25 Скажите, а кто первым подумал измерять высоту предмета по его тени . Рассказывают, что египетский фараон Амазис приказал измерить высоту пирамиды Хеопса. Жрецы не знали, как выполнить эту задачу. И тогда им на помощь пришел Фалес. Собравшиеся у подножия пирамиды жрецы с интересом следили за действиями милетского мудреца, который очертил вокруг себя окружность, радиус которой был равен его росту. Фалес стал в центре окружности и стал дожидаться, когда конец его тени достигнет окружности. Когда это произошло, Фалес быстро направился к месту на земле, где заканчивалась тень пирамиды, и положил там камень. Фалес справедливо считал, что в этот момент и тень от пирамиды равна высоте самой пирамиды. Затем Фалес измерил расстояние от камня до подножия пирамиды, прибавил к этому расстоянию половину длины основания пирамиды и огласил результат своего труда

Итог урока . И в заключении давайте проведём небольшой итоговый тест.

( ПРИЛОЖЕНИЕ 5) За каждый правильный ответ 1 балл. ( Проверка через документ- камеру)

Давайте посмотрим в ваших листах самооценки, сколько баллов вы набрали за урок . Выставление отметок.

Ребята, все опорные конспекты и задания вложите в папку для подготовки к ОГЭ . Тренировочные задания нужно выполнить с индивидуально- групповому занятию.

И закончить наш урок мне бы хотелось словами Фалеса Милетского : «Блаженство тела состоит в здоровье, блаженство ума – в знании». Спасибо всем за урок.

Приложение 1

Дата _____________ Классная работа ________________________________________

1. О т столба к дому натянут провод длиной 17 м, который закреплён на стене дома на вы­соте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м. Ответ дайте в метрах.

№ 2 Найти радиус окружности, если АВ = 12см, ОА = 13см.

№ 3 Лестница соединяет точки A и B и состоит из 15 ступеней. Высота каждой ступени равна 28 см, а длина - 96 см. Найдите расстояние ме­жду точками A и B (в метрах).

№ 4 На рисунке изображён колодец с «журавлём». Корот­кое плечо имеет длину 2 м, а длинное плечо - 5 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?

№ 5 Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря.

№ 6 На каком рас­стоянии (в метрах) от фонаря стоит че­ловек ростом 1,6 м, если длина его тени равна 8 м, высота фонаря 5 м?

№ 7 Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в см) от проектора нужно расположить экран B вы­сотой 320 см, чтобы он был полностью освещён, ес­ли настройки проектора остаются неизменными?

Приложение 2

Приложение 3

Приложение 4

Лист самооценки ученика

№п/п	Вид работы	Кол – во баллов
1.	Математический диктант
2.	Задачи на теорему Пифагора
3.	Устное решение задач
4.	Итоговый тест
	Итого:

Критерии отметки: менее 10 баллов – «2»

10 – 14 баллов - «3»

15-18 баллов - «4»

более 18 баллов – «5»

Приложение 5

Итоговый тест Вариант 1

1. Если стороны одного треугольника пропорциональны сторонам другого треугольника, то треугольники:

а) равны; б) подобны; в) нет ответа (1 балл) 2. Если треугольники подобны, то : а) стороны равны; б) углы пропорциональны; в) углы равны (1 балл) 3. Углы треугольника равны 20⁰, 40⁰, А⁰. Угол, соответствующий углу А подобного треугольника, равен: а) 40⁰; б) 120⁰; в) 60⁰ ; г) 20⁰ (2 балла) 4 . По какому признаку ∆AВО подобен ∆СДО, если В = Д: а) II; б) I; в) III (2 балла)







Итоговый тест Вариант 2 1.Если углы одного треугольника равны углам другого треугольника, то треугольники: а) подобны; б) нет ответа; в) равны; (1 балл) 2. Если треугольники подобны, то : а) стороны пропорциональны; б) стороны равны; в) углы пропорциональны (1 балл) 3. Стороны треугольника равны 15см, 21см, 30см. Две стороны подобного ему треугольника – 10 см и 5 см. Длина третьей стороны: а) 7см; б) 3см; в) 12см ; г) 10см (2 балла) 4 . По какому признаку ∆AВО подобен ∆СДО, если В= Д: а) II; б) I; в) III (2 балла)

8