"Изучение и освоение технологических приемов выполнения развертки бумажных изделий"

Изучение и освоение технологических приемов выполнения развертки бумажных изделий».

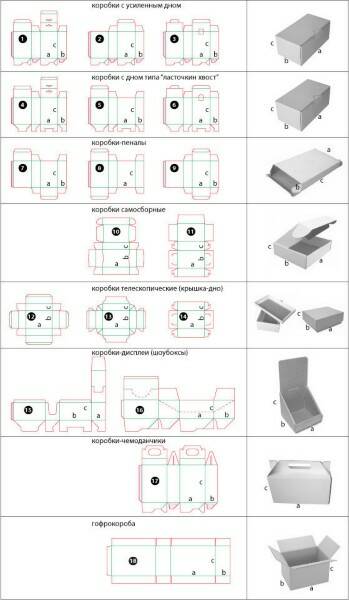
РАЗВЕРТКИ имеют большое применение на машиностроительных заводах, обувных фабриках, в швейных мастерских, а также при изготовлении всевозможной тары (пакеты, коробки и т.п.) Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки.

РАЗВЕРТКОЙ называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью.

При построении развертки надо знать сначала истинные, натуральные размеры и форму отдельных элементов предмета на чертеже. В простейших случаях развертки можно вычертить, не пользуясь проекциями предмета. Например, для построения развертки куба достаточно знать размер одного ребра куба.

Рассмотрим построение разверток поверхности некоторых простейших тел.

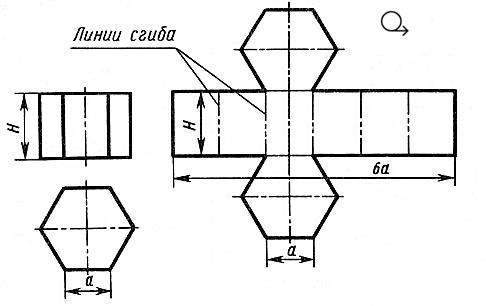
Рис 1. Развертка поверхности прямой шестиугольной призмы

Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т. е.6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований - два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба - штрихпунктирной с двумя точками.

Подобным образом можно построить развертки прямых призм с любой фигурой в основании.

Развертка поверхности правильной пирамиды представляет собой плоскую фигуру, составленную из боковых граней - равнобедренных или равносторонних треугольников и правильного многоугольника основания. Для примера представлены развёртки правильной четырехугольной пирамиды (рис. 2) и правильной пятиугольной пирамиды (рис. 3).

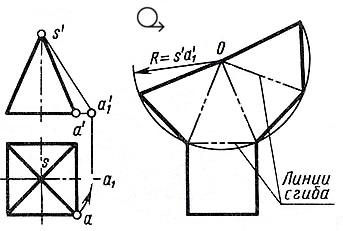
Рис 2. Развертка поверхности правильной четырёхугольной пирамиды

Решение задачи осложняется тем, что неизвестна величина боковых граней пирамиды, так как ребра граней не параллельны ни одной из плоскостей проекций. Поэтому построение начинают с определения истинной величины наклонного ребра SA. Определив способом вращения (см. рис. 8) истинную длину наклонного ребра SA, равную s'a'₁, из произвольной точки О, как из центра, проводят дугу радиусом s'a'₁. На дуге откладывают четыре отрезка, равные стороне основания пирамиды, которое спроецировано на чертеже в истинную величину. Найденные точки соединяют прямыми с точкой О. Получив развертку боковой поверхности, к основанию одного из треугольников пристраивают квадрат, равный основанию пирамиды.

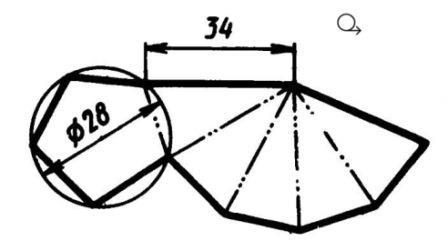
Рис 3. Развертка поверхности правильной пятиугольной пирамиды

Развертка поверхности прямого кругового конуса представляет собой плоскую фигуру, состоящую из кругового сектора и круга (рис. 4).

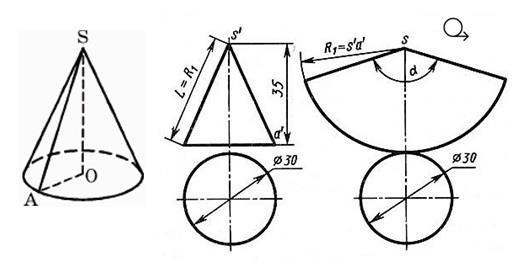
Рис 4. Развертка поверхности прямого кругового конуса

Развертка цилиндра представляет собой прямоугольник, одна сторона которого равна высоте цилиндра, а другая – развернутой длине окружности основания 2πR (рис. 5).

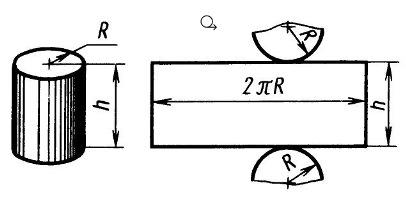
Рис. 5 Развертка поверхности прямого цилиндра

На картах мира (рис. 6) земной шар изображается в виде кругов — восточного и западного полушария. Развертка шара – круг или, точнее, два круга?

Попытаемся развернуть и совместить с плоскостью шаровую поверхность. Сделать это без складок и разрывов не удастся. Многие геометрические фигуры легко развертываются в плоскость, а шар – нет.

Если поверхность глобуса разрезать вдоль меридианов на маленькие дольки (сегменты) и выпрямить их, то в каждой из этих выпрямленных долек мы можем не заметить никаких видимых искажений. Но развертку мы получим с разрывом (рис. 6).

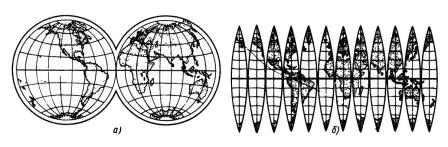
Рис. 6. Географическая карта

Именно такие «дольки» нарезают по контуру и наклеивают одну возле другой на поверхность школьного глобуса. Присмотритесь к глобусу, и вы убедитесь, что это так.

Чтобы получить карту без разрыва, приходится допускать некоторые неточности, которые сводятся к искажению направлений, расстояний и площадей, неодинаковых в разных частях карты.

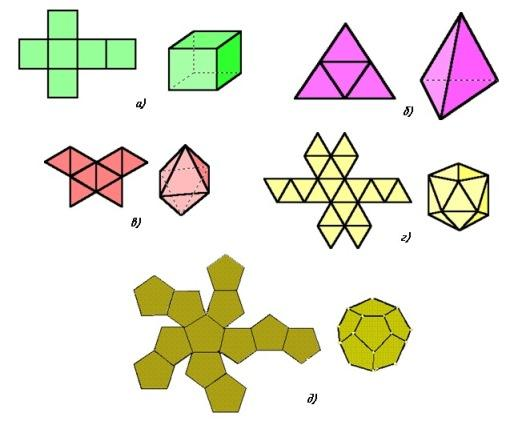
Развёртки некоторых правильных многогранников представлены на рисунке:

а) куб, б) тетраэдр, в) октаэдр, г) икосаэдр, д) додекаэдр.