1. Тема лекции: Частотная модуляция
План лекции:
Частотная модуляция
Математическая модель ЧМ-сигнала.
Спектр амплитуд ЧМ-сигнала.
1. Частотная модуляция
Частотная модуляция – это процесс изменения частоты несущего высокочастотного колебания в соответствии с законом изменения мгновенных значений модулирующего низкочастотного сигнала.
Пусть модулирующий сигнал UM (см. рис. 1а), является гармоническим колебанием с частотой F, амплитудой UmM и начальной фазой равной нулю, т.е.
UM=UmMsin2Ft=UmMsint (1.1)
где – угловая частота модулирующего колебания.
В качестве несущего колебания в электросвязи обычно используют также гармонические колебания UH (см. рис. 1б) с амплитудой UMH, высокой частотой fH и начальной фазой равной нулю, т.е.
UH=UMHsinHt (1.2)
На рис. 1 приведены временные диаграммы, полученные на основании определения частотной модуляции и поясняющие процесс формирования ЧМ сигнала.
На временном интервале от 0 до t1 модулирующее напряжение UM(t)=0, следовательно, отсутствует причина, вызывающая изменение частоты несущих колебаний. Поэтому на этом временном интервале частота ЧМ сигнала должна быть равна частоте несущих колебаний (см. рис. 1в).
В момент времени t1 появляется модулирующий сигнал, частота несущих колебаний должна изменяться. Предположим, положительные мгновенные значения UM вызывают увеличение, а отрицательный – уменьшение частоты несущей на некоторую величину  f пропорциональную величине UM (см. рис. 1в). Временная диаграмма ЧМ сигнала приведена на рис. 1г.
f пропорциональную величине UM (см. рис. 1в). Временная диаграмма ЧМ сигнала приведена на рис. 1г.

Рис. 1. Временные диаграммы
2. Математическая модель ЧМ сигнала.
Согласно рис. 1 амплитуда ЧМ сигнала в процессе модуляции не меняется и равна амплитуде несущих колебаний UMH, поэтому математическая модель ЧМ сигнала в общем виде может быть записана так:
UЧM(t)=UMHsin ЧM(t) (2.1)
ЧM(t) (2.1)
где  ЧM(t) – полная фаза ЧМ сигнала.
ЧM(t) – полная фаза ЧМ сигнала.
Согласно рис. 1 частота ЧМ сигнала должна меняться по закону
FЧM(t)=fH +  fgsint (2.2)
fgsint (2.2)
ЧM(t)= H +  gsint (2.3)
gsint (2.3)
где  fg – максимальное отклонение частоты ЧМ сигнала от несущей частоты fH в процессе модуляции называется девиацией частоты.
fg – максимальное отклонение частоты ЧМ сигнала от несущей частоты fH в процессе модуляции называется девиацией частоты.
 g=2
g=2 fg – девиация угловой частоты.
fg – девиация угловой частоты.
Индекс частотной модуляции М: эта величина прямо пропорциональна амплитуде UmM модулирующего гармонического сигнала и обратно пропорциональна его угловой частоте .
Если в (2.1) ввести обозначения (2.2) и (2.3), то получим математическую модель ЧМ сигнала при гармоническом модулирующем сигнале
UЧM(t)=UMHsin(Ht – Мcos t) (2.4)
Анализ уравнения (2.4) показывает, что ЧМ всегда сопровождается фазовой модуляцией, при этом индекс частотной модуляции М равен амплитуде изменения фазы – девиации фазы.
3. Спектр амплитуд ЧМ сигнала.
Получение спектра амплитуд любого сигнала сводится к получению представления этого сигнала в виде суммы гармонических колебаний.
Таким образом, даже для однотональной ЧМ спектр является сложным. Спектр содержит первый член – гармоническая составляющая с частотой несущей, вторая группа гармонических составляющих с частотами fH – kF является нижней боковой полосой частот, третья группа составляющих с частотами fH + kF представляет нижнюю боковую полосу частот. Число верхних и нижних боковых частот теоретически бесконечно. Боковые гармонические колебания расположены симметрично относительно 0 на расстоянии . Амплитуды всех компонент спектра, в том числе 0, пропорциональны Jk(m).
Для детального анализа и построения спектральных диаграмм необходимо знание функций Бесселя Jk(m) при различных значениях k и m. их можно найти в математических справочниках. На рис. 2 приведены графики функций Бесселя при k, m 8.
8.
На практике считают, что можно пренебречь всеми спектральными составляющими, номера которых km+1 (уровень меньше 5% от уровня несущей).
Таким образом, ширина спектра ЧМ сигнала в значительной степени зависит от индекса ЧМ. Если М 5, то частотная модуляция является широкополосной.

Рис.2. Графики функций Бесселя
Вопросы для самоконтроля
1. Что такое частотная модуляция?
2. Физический смысл девиации частоты при ЧМ
3. Каким требованиям должны удовлетворять несущие колебания?
2. Методические указания к выполнению практической работы
«Расчет и построение спектра частотно-модулированного сигнала»
Цель работы: закрепить теоретический материал и выработать умения при расчете и построении спектра ЧМ сигнала.
Рекомендуемая литература:
Костров Б. В. Технологии физического уровня передачи данных. Учебник, -М.: Издательский центр «Академия», 2018. - 224с.
Ушаков П.А. Цепи и сигналы электросвязи. Учебник. –М.: Издательский центр «Академия», 2010. – 352с.
Пример расчета.
Пусть даны следующие условия: 
 .
.
Алгоритм расчета:
Определить период колебаний модулирующей частоты:

2. Определить значение модулирующей частоты:

Определить девиацию частоты:

Значение несущей частоты равно:



Построить временную диаграмму ЧМ сигнала:
Выбирается масштаб по оси времени; для этого выделяем для изображения одного периода модулирующего колебания 10 см, тогда масштаб по времени:

б) Выбирается масштаб по оси частот, для этого выделяем для изображения девиации частоты 1 см, тогда масштаб по частоте  будет:
будет:

Отметим, что отсчет по вертикальной оси начинается не с нуля. Временная диаграмма ЧМ сигнала приведена на рис. 1.
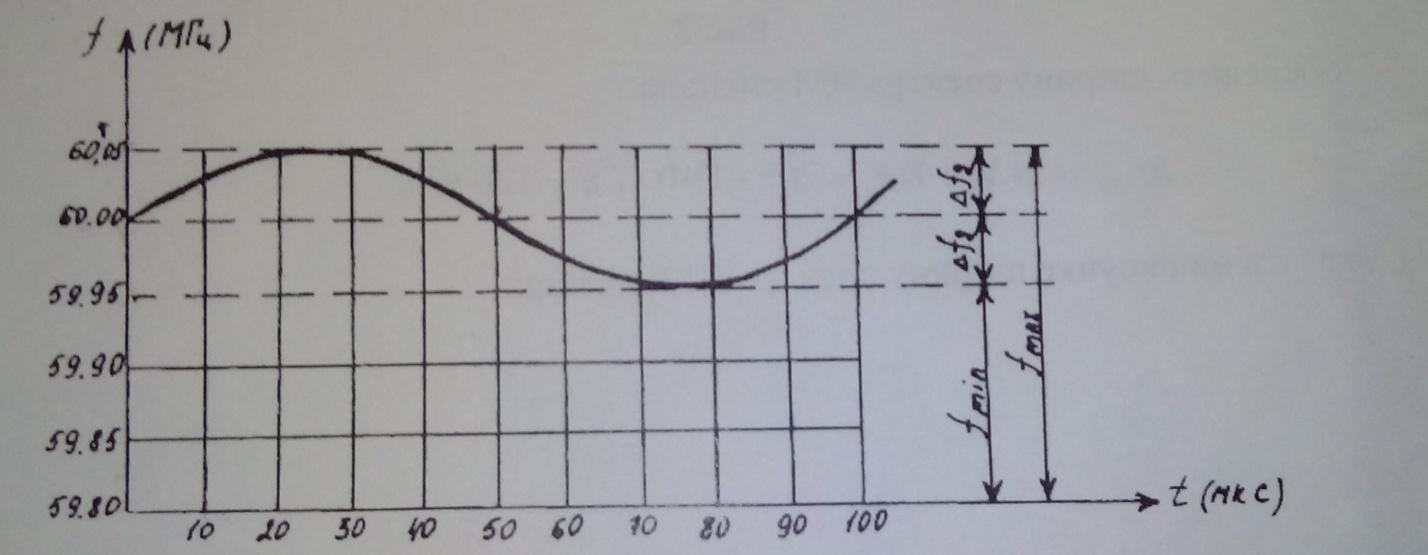
Рис. 1. Временная диаграмма ЧМ-сигнала
Определить по графикам значения функций Бесселя для индекса частотной модуляции М= 5 (см. рис. 2 в лекции)







Определить амплитуду составляющих ЧМ сигнала:
Рассчитать значения частот, составляющих ЧМ сигнал:
Построить в масштабе спектр амплитуд.

Определить ширину спектра ЧМ сигнала.
Указать на рисунке ширину спектра ЧМ сигнала
ЗАДАНИЕ:
| Вариант | 
| Ω, рад/с | M | 
|
| 1 | 60 | 2.5π | 1 | 50π |
| 2 | 60 | 2.5π | 2 | 60π |
| 3 | 60 | 2.5π | 3 | 70π |
| 4 | 60 | 2.5π | 4 | 80π |
| 5 | 60 | 2.5π | 5 | 90π |
| 6 | 50 | 2π  | 1 | 50π |
| 7 | 50 | 2π  | 2 | 60π |
| 8 | 50 | 2π  | 3 | 70π |
| 9 | 50 | 2π  | 4 | 80π |
| 10 | 50 | 2π  | 5 | 90π |
| 11 | 40 | 1.5π | 1 | 50π |
| 12 | 40 | 1.5π | 2 | 60π |
| 13 | 40 | 1.5π | 3 | 70π |
| 14 | 40 | 1.5π | 4 | 80π |
| 15 | 40 | 1.5π | 5 | 90π |
| 16 | 30 | π | 1 | 50π |
| 17 | 30 | π | 2 | 60π |
| 18 | 30 | π | 3 | 70π |
| 19 | 30 | π | 4 | 80π |
| 20 | 30 | π | 5 | 90π |
| 21 | 20 | 3π | 1 | 50π |
| 22 | 20 | 3π | 2 | 60π |
| 23 | 20 | 3π | 3 | 70π |
| 24 | 20 | 3π | 4 | 80π |
| 25 | 20 | 3π | 5 | 90π |
| 26 | 20 | 3π | 1 | 50π |
| 27 | 10 | 0.5π | 2 | 60π |
| 28 | 10 | 0.5π | 3 | 70π |
| 29 | 10 | 0.5π | 4 | 80π |
| 30 | 10 | 0.5π | 5 | 90π |
| 31 | 10 | 0.5π | 1 | 50π |
| 32 | 10 | 0.5π | 2 | 60π |





 f пропорциональную величине UM (см. рис. 1в). Временная диаграмма ЧМ сигнала приведена на рис. 1г.
f пропорциональную величине UM (см. рис. 1в). Временная диаграмма ЧМ сигнала приведена на рис. 1г.


 .
.






 будет:
будет:












