Муниципальное бюджетное общеобразовательное учреждение
"Основная общеобразовательная школа с Саклово"
| Рассмотрено на заседании ШМО Протокол № _1 от 28.08.2020 г Руководитель: О.Н. Сапранькова | Согласовано: Заместитель директора по УВР __________ Н.Н Галиева 31.08.2020 г. | Утверждаю: Директор МБОУ ООШ с. Саклово __________ Р.М.Газиев Приказ № от 31.08.2020 г. |
Муниципального района Краснокамский район Республики Башкортостан
КАЛЕНДАРНО ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
по алгебре
для 8 класса
на 2020 – 2021 учебный год
Составитель : Галиева Назлия Нурсагитовна
учитель высшей квалификационной категории
Саклово. 2020 год
Пояснительная записка
Программа рассчитана на 3 часа в неделю в каждом классе, всего 105 часов и соответствует федеральному государственному образовательному стандарту основного общего образования.
Программа по алгебре составлена на основе Фундаментального ядра содержания общего образования, требований к результатам освоения образовательной программы основного общего образования, представленных в федеральном государственном образовательном стандарте основного общего образования, с учётом преемственности с примерными программами для начального общего образования по математике. В ней также учитываются доминирующие идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности и способствуют формированию ключевой компетенции — умения учиться.
Курс алгебры 7-9 классов является базовым для математического образования и развития школьников. Алгебраические знания и умения необходимы для изучения геометрии в 7-9 классах, алгебры и математического анализа в 10-11 классах, а также изучения смежных дисциплин.
Практическая значимость школьного курса алгебры 7 - 9 классов состоит в том, что предметом его изучения являются количественные отношения и процессы реального мира, описанные математическими моделями. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.
Одной из основных целей изучения алгебры является развитие мышления, прежде всего формирование абстрактного мышления. В процессе изучения алгебры формируется логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию.
Обучение алгебре даёт возможность школьникам научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения.
В процессе изучения алгебры школьники учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у учащихся грамотную устную и письменную речь.
Знакомство с историей развития алгебры как науки формирует у учащихся представления об алгебре как части общечеловеческой культуры.
Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируются содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения, демонстрация возможностей применения теоретических знаний для решения разнообразных задач прикладного характера, например решения текстовых задач, денежных и процентных расчётов, умение пользоваться количественной информацией, представленной в различных формах, умение читать графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определённого типа.
Планируемые результаты обучения алгебре в 7-9 классах
Алгебраические выражения
Учащийся научится:
оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные, работать с формулами;
оперировать понятием "квадратный корень", применять его в вычислениях;
выполнять преобразование выражений, содержащих степени с натуральными показателями;
выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
выполнять разложение многочленов на множители.
Учащийся получит возможность:
выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования для решения задач из различных разделов курса.
Уравнения
Учащийся научится:
решать линейные уравнения с одной переменной, системы двух уравнений с двумя переменными;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.
Учащийся получит возможность:
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
Неравенства
Учащийся научится:
понимать терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность:
освоить разнообразные приѐмы доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач, задач из смежных предметов и практики;
применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
Числовые множества
Выпускник научится:
понимать терминологию и символику, связанные с понятием множества, выполнять операции над множествами;
использовать начальные представления о множестве действительных чисел.
Выпускник получит возможность:
развивать представления о множествах;
развивать представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
Функции
Учащийся научится:
• понимать и использовать функциональные понятия, язык (термины, символические обозначения);
строить графики элементарных функций, исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами;
понимать и использовать язык последовательностей (термины, символические обозначения);
применять формулы, связанные с арифметической и геометрической прогрессиями, и аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.
Учащийся получит возможность:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить боле сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач израз личных разделов курса;
решать комбинаторные задачи с применением формулы n–го члена и суммы n первых членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;
понимать арифметическую и геометрическую прогрессии как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую – с экспоненциальным ростом.
Элементы прикладной математики
Выпускник научится:
использовать в ходе решения задач элементарные представления, связанные с приближѐнными значениями величин;
использовать простейшие способы представления и анализа статистических данных;
находить относительную частоту и вероятность случайного события;
решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность:
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных;
приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы;
приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов;
научиться некоторым специальным приёмам решения комбинаторных задач.
Содержание курса алгебры 8 класса
Алгебраические выражения
Рациональные выражения. Свойства степени с целым показателем. Квадратный трѐхчлен. Корень квадратного трѐхчлена. Свойства квадратного трѐхчлена. Разложение квадратного трѐхчлена на множители. Квадратные корни.
Уравнения
Равносильные уравнения. Уравнение как математическая модель реальной ситуации. Квадратное уравнение. Формула корней квадратного уравнения. Теорема Виета. Рациональные уравнения. Решение рациональных уравнений, сходящихся к линейным или квадратным уравнениям.
Числовые множества
Множество и его элементы. Способы задания множеств. Равные множества. Пустое множество. Подмножество. Операции над множествами. Иллюстрация соотношений между множествами с помощью диаграмм Эйлера. Множества натуральных, целых, рациональных чисел.
Функции
Числовые функции
Функциональные зависимости между величинами. Понятие функции. Функция как математическая модель реального процесса. Область определения и область значения функции. Способы задания функции. График функции. Построение графиков функций с помощью преобразований фигур. Нули функции. Промежутки знакопостоянства функции. Промежутки возрастания и убывания функции. Обратная пропорциональность, квадратичная функция, функция у = √х, их свойства и графики.
Алгебра в историческом развитии
Из истории возникновения формул для решения уравнений 3-й и 4-й степеней. История развития понятия функции. Числа Фибоначчи. Задача Л. Пизанского (Фибоначчи) о кроликах. Л.Ф. Магницкий, П.Л. Чебышев, Н.И. Лобачевский, В.Я. Буняковский, А.Н. Колмагоров, Ф. Виет, П. Ферма, Р. Декарт, Н. Тарталья, Д. Кардано, Н. Абель, Б. Паскаль, Л. Пизанский, К. Гаусс.
Календарно- тематическое планирование. Алгебра. 8 класс
3 часа в неделю, всего 105 часов.
|
№ |
Тема и содержание урока |
Основные виды деятельности |
Кол-во часов | Дата |
| По пла ну | фактическая |
|
|
Глава 1 Рациональные выражения |
|
44 |
|
|
| 1-2 | Рациональные дроби | Распознавать целые рациональные выражения, дробные рациональные выражения, приводить примеры таких выражений. Формулировать: определения: рационального выражения, допустимых значений переменной, тождественно равных выражений, тождества, равносильных уравнений, рационального уравнения, степени с нулевым показателем, степени с целым отрицательным показателем, стандартного вида числа, обратной пропорциональности; свойства: основное свойство рациональной дроби, свойства степени с целым показателем, уравнений, функции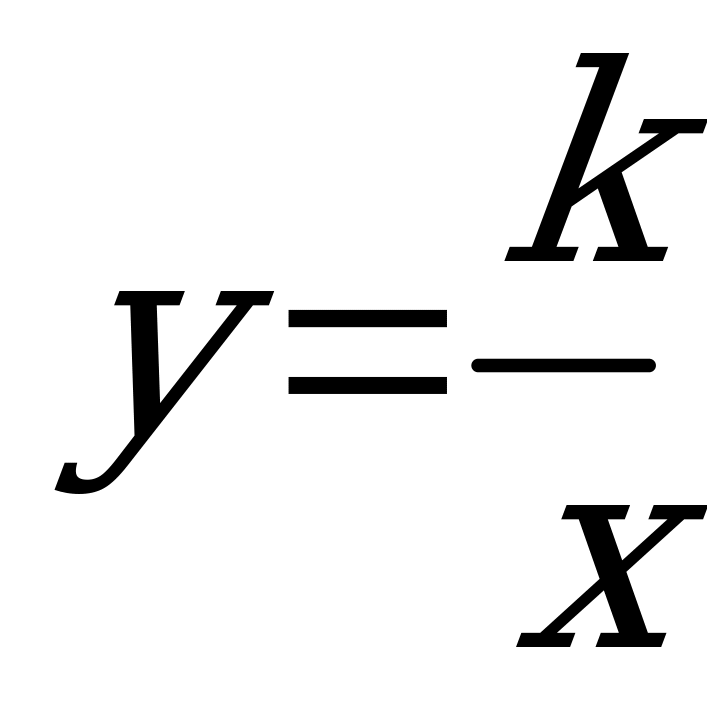 ; ; правила: сложения, вычитания, умножения, деления дробей, возведения дроби в степень; условие равенства дроби нулю. Доказывать свойства степени с целым показателем. Описывать графический метод решения уравнений с одной переменной. Применять основное свойство рациональной дроби для сокращения и преобразования дробей. Приводить дроби к новому (общему) знаменателю. Находить сумму, разность, произведение и частное дробей. Выполнять тождественные преобразования рациональных выражений. Решать уравнения с переменной в знаменателе дроби. Применять свойства степени с целым показателем для преобразования выражений. Записывать числа в стандартном виде. Выполнять построение и чтение графика функции 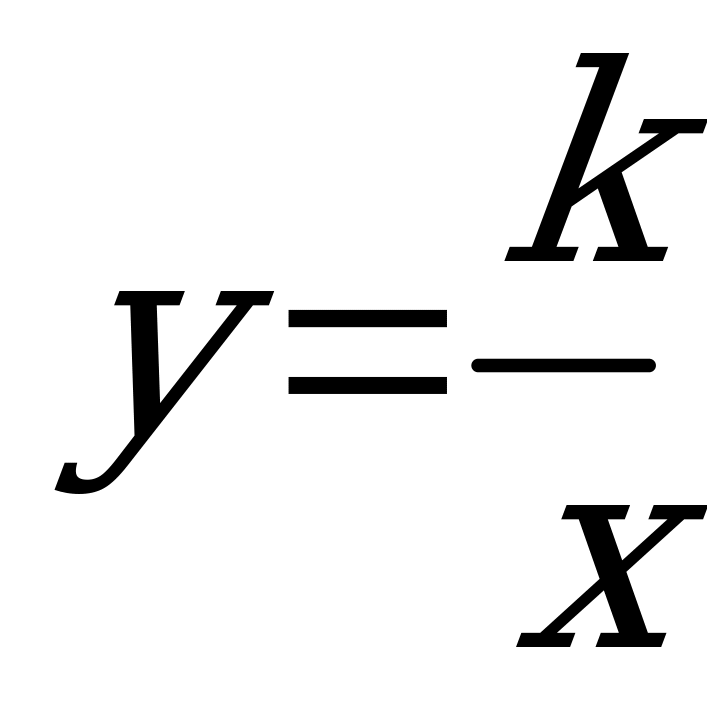 | 2 |
|
|
| 3 | Основное свойство рациональной дроби | 1 |
|
|
| 4 | Решение упражнений на основное свойство рациональной дроби | 1 |
|
|
| 5 | Решение задач на основное свойство рациональной дроби | 1 |
|
|
| 6 | Сложение рациональных дробей с одинаковыми знаменателями | 1 |
|
|
| 7 | Вычитание рациональных дробей с одинаковыми знаменателями | 1 |
|
|
| 8 | Решение упражнений на сложение и вычитание рациональных дробей с одинаковыми знаменателями | 1 |
|
|
| 9 | Сложение рациональных дробей с разными знаменателями | 1 |
|
|
| 10 | Вычитание рациональных дробей с разными знаменателями | 1 |
|
|
| 11 | Решение упражнений на сложение и вычитание рациональных дробей с разными знаменателями | 1 |
|
|
| 12 | Решение задач на сложение и вычитание рациональных дробей с разными знаменателями | 1 |
|
|
| 13 | Закрепление знаний по теме: "Сложение и вычитание рациональных дробей с разными знаменателями" | 1 |
|
|
| 14 | Повторение и систематизация учебного материала. | 1 |
|
|
| 15 | Контрольная работа № 1 | 1 |
|
|
| 16 | Умножение рациональных дробей. Возведение рациональной дроби в степень | 1 |
|
|
| 17 | Деление рациональных дробей. | 1 |
|
|
| 18 | Возведение рациональной дроби в степень | 1 |
|
|
| 19 | Решение упражнений на умножение и деление рациональных дробей, возведение рациональной дроби в степень. | 1 |
|
|
| 20-21 | Тождественные преобразования рациональных выражений | 2 |
|
|
| 22-23 | Выполнение тождественных преобразований рациональных выражений. | 2 |
|
|
| 24 | Решение упражнений по теме:" Тождественные преобразования рациональных выражений". | 1 |
|
|
| 25 | Закрепление знаний на выполнение тождественных преобразований рациональных выражений. | 1 |
|
|
| 26 | Повторение и систематизация учебного материала. | 1 |
|
|
| 27 | Контрольная работа № 2 | 1 |
|
|
| 28 | Равносильные уравнения. | 1 |
|
|
| 29 | Рациональные уравнения | 1 |
|
|
| 30 | Решение равносильных и рациональных уравнений. | 1 |
|
|
| 31-32 | Степень с целым отрицательным показателем | 2 |
|
|
| 33 | Преобразование выражений, содержащих степень с целым отрицательным показателем. | 1 |
|
|
| 34 | Решение упражнений по теме: "Степень с целым отрицательным показателем" | 1 |
|
|
| 35-36 | Свойства степени с целым показателем | 2 |
|
|
| 37 | Применение свойств степени с целым показателем | 1 |
|
|
| 38 | Преобразование выражений, используя свойства степени с целым показателем | 1 |
|
|
| 39 | Свойства степени с целым показателем | 1 |
|
|
| 40 | Функция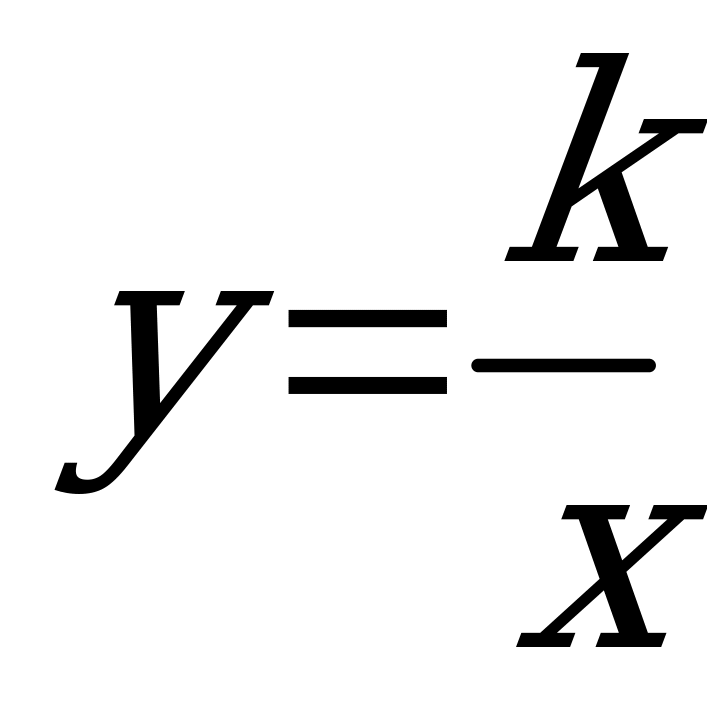 и её график и её график | 1 |
|
|
| 41-42 | Построение и чтение графика функции 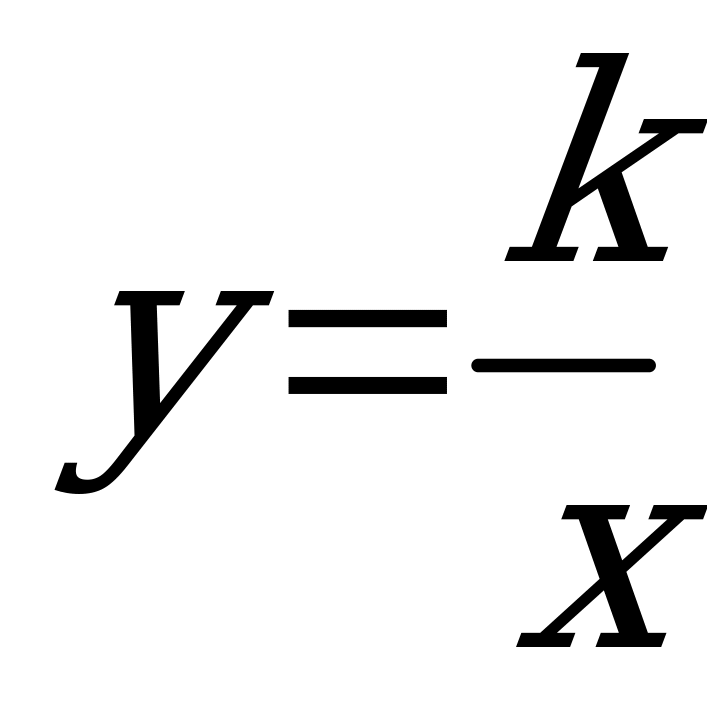 | 2 |
|
|
| 43 | Повторение и систематизация учебного материала. | 1 |
|
|
| 44 | Контрольная работа № 3 | 1 |
|
|
|
| Глава 2
Квадратные корни.
Действительные числа | 25 |
|
|
| 45-46 | Функция y = x2
и её график | Описывать: понятие множества, элемента множества, способы задания множеств; множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел и связи между этими числовыми множествами; связь между бесконечными десятичными дробями и рациональными, иррациональными числами. Распознавать рациональные ииррациональные числа. Приводить примеры рациональных чисел и иррациональных чисел. Записывать с помощью формул свойства действий с действительными числами. Формулировать: определения: квадратного корня из числа, арифметического квадратного корня из числа, равных множеств, подмножества, пересечения множеств, объединения множеств; свойства: функции y = x2, арифметического квадратного корня, функции 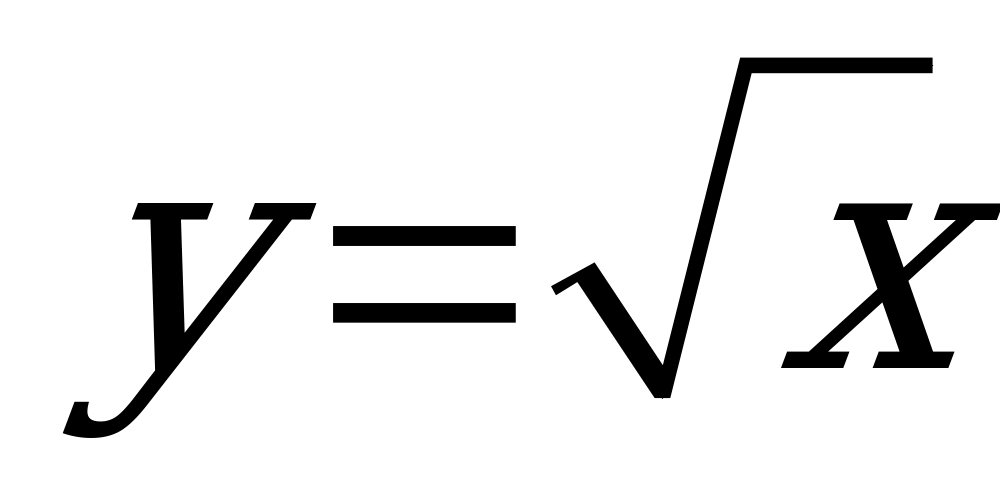 . . Доказывать свойства арифметического квадратного корня. Строить графики функций y = x2и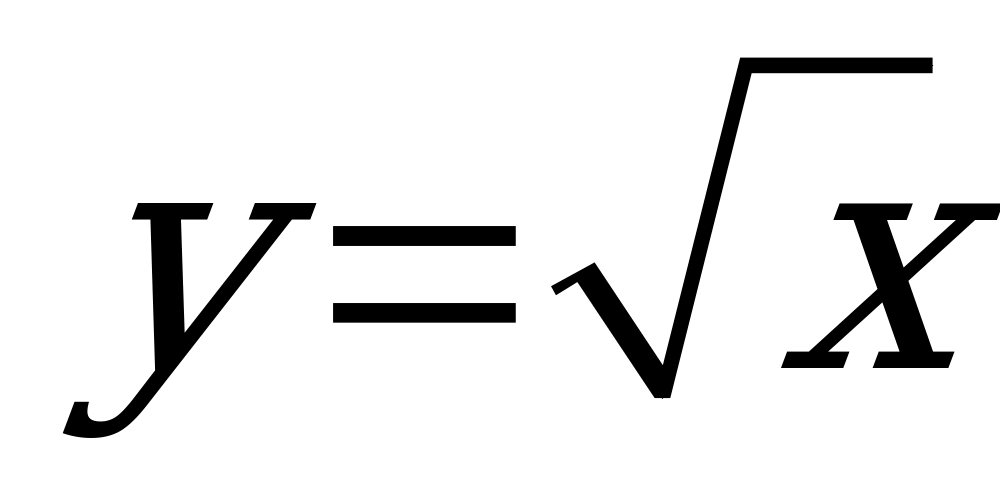 . . Применять понятие арифметического квадратного корня для вычисления значений выражений. Упрощать выражения, содержащие арифметические квадратные корни. Решать уравнения. Сравнивать значения выражений. Выполнять преобразование выражений с применением вынесения множителя из-под знака корня, внесения множителя под знак корня. Выполнять освобождение от иррациональности в знаменателе дроби, анализ соотношений между числовыми множествами и их элементами | 2 |
|
|
| 47 | Решение задач, используя свойства функции y = x2
и её график. | 1 |
|
|
| 48 | Квадратные корни. Арифметический квадратный корень. | 1
|
|
|
| 49 | Применение формул сокращенного умножения при действии с корнями.
| 2 |
|
|
| 50 | Решение упражнений по теме: "Квадратные корни. Арифметический квадратный корень" | 1 |
|
|
| 51-52 | Множество и его элементы | 2
|
|
|
| 53-54 | Подмножество. Операции над множествами | 2 |
|
|
| 55-56 | Числовые множества | 1
|
|
|
| 57 | Свойства арифметического квадратного корня
| 1 |
|
|
| 58-59 | Решение упражнений на свойства арифметического квадратного корня
| 2 |
|
|
| 60 | Применение основных правил действия с арифметическим квадратным корнем при упрощении выражений.
| 1 |
|
|
| 61-62 | Тождественные преобразования выражений, содержащих квадратные корни
| 2 |
|
|
| 63-64 | Решение упражнений на тождественные преобразования выражений, содержащих квадратные корни
| 2 |
|
|
| 65 | Закрепление знаний по тождественным преобразованиям выражений, содержащих квадратные корни
| 1 |
|
|
| 66 | Функция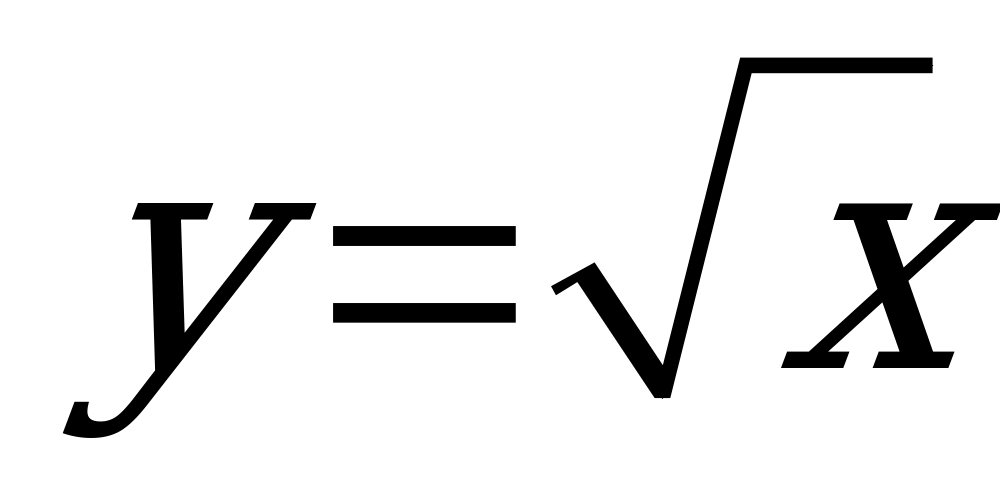
и её график | 1 |
|
|
| 67 | Построение и чтение графика функции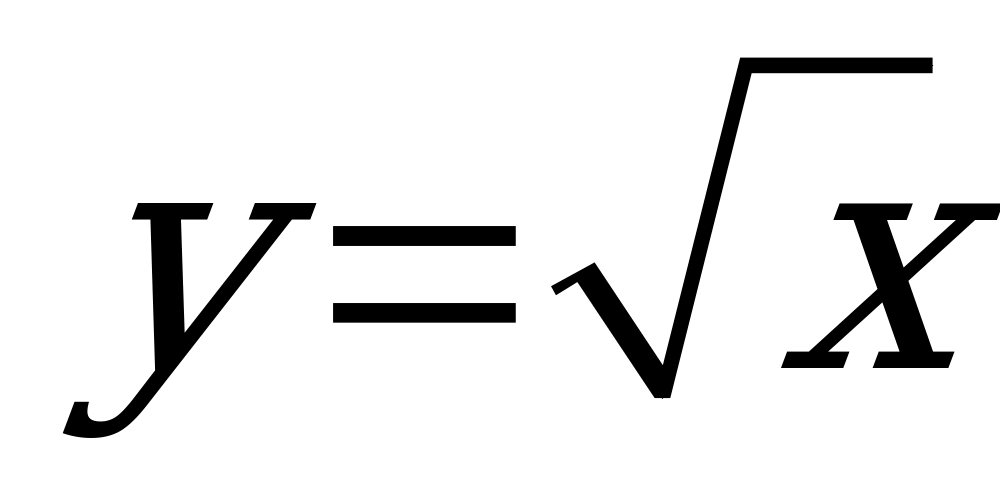
| 1 |
|
|
| 68 | Повторение и систематизация учебного материала.
| 1 |
|
|
| 69 | Контрольная работа № 4 | 1 |
|
|
|
| Глава 3 Квадратные уравнения |
| 26 |
|
|
| 70 | Квадратное уравнение и его корни. | Распознавать и приводить примеры квадратных уравнений различных видов (полных, неполных, приведённых), квадратных трёхчленов. Описывать в общем виде решение неполных квадратных уравнений. Формулировать: определения: уравнения первой степени, квадратного уравнения; квадратного трёхчлена, дискриминанта квадратного уравнения и квадратного трёхчлена, корня квадратного трёхчлена; биквадратного уравнения; свойства квадратного трёхчлена; теорему Виета и обратную ей теорему. Записывать и доказывать формулу корней квадратного уравнения. Исследовать количество корней квадратного уравнения в зависимости от знака его дискриминанта. Доказывать теоремы: Виета (прямую и обратную), о разложении квадратного трёхчлена на множители, о свойстве квадратного трёхчлена с отрицательным дискриминантом. Описывать на примерах метод замены переменной для решения уравнений. Находить корни квадратных уравнений различных видов. Применять теорему Виета и обратную ей теорему. Выполнять разложение квадратного трёхчлена на множители. Находить корни уравнений, которые сводятся к квадратным. Составлять квадратные уравнения и уравнения, сводящиеся к квадратным, являющиеся математическими моделями реальных ситуаций | 1 |
|
|
| 71 | Неполные квадратные уравнения | 1 |
|
|
| 72 | Решение неполных квадратных уравнений | 1 |
|
|
| 73 | Формула корней квадратного уравнения | 1 |
|
|
| 74-75 | Решение квадратных уравнений через дискриминант | 2 |
|
|
| 76 | Решение квадратных уравнений с параметрами | 1 |
|
|
| 77 | Теорема Виета | 1 |
|
|
| 78 | Решение задач, используя теорему Виета | 1 |
|
|
| 79 | Повторение и систематизация учебного материала | 1 |
|
|
| 80 | Контрольная работа № 5 | 1 |
|
|
| 81 | Квадратный трёхчлен | 1 |
|
|
| 82 | Разложение квадратного трехчлена на множители. |
1 |
|
|
| 83 | Решение упражнений по теме: «Квадратный трехчлен» | 1 |
|
|
| 84 | Решение биквадратных уравнений. | 1 |
|
|
| 85. | Дробно-рациональные уравнения, сводящиеся к квадратным. | 1 |
|
|
| 86-88 | Решение уравнений, сводящихся к квадратным уравнениям | 3 |
|
|
| 89-91 | Рациональные уравнения как математические модели реальных ситуаций | 3 |
|
|
| 92-93 | Решение задач с помощью квадратных уравнений. | 2 |
|
|
| 94 | Повторение и систематизация учебного материала. | 1 |
|
|
| 95 | Контрольная работа № 6 | 1 |
|
|
|
| Повторение и систематизация
учебного материала |
| 10 |
|
|
| 96-103 | Упражнения для повторения курса 8 класса |
| 8 |
|
|
| 104 | Контрольная работа № 7
|
| 1 |
|
|
| 105 | Итоговое занятие по курсу 8 класса
|
| 1 |
|
|















