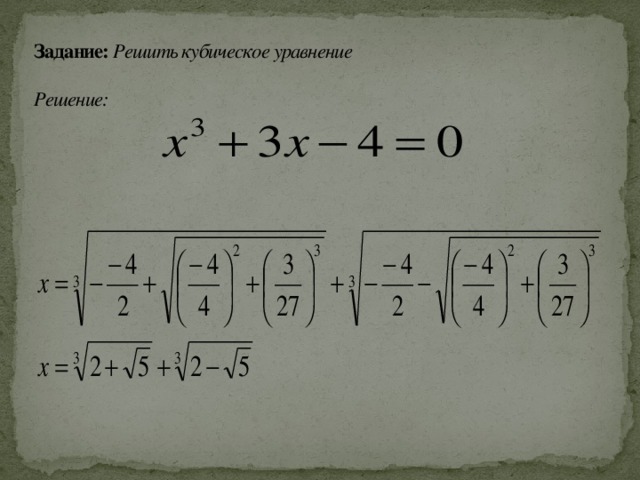СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 02.06.2025 15:17

Чебанова Елена Ильинична
29 лет
Местоположение
Россия, Сургут
Специализация
Кардано и его исследования кубического уравнения
Категория:
Математика
12.11.2016 20:31



 0: Свой способ решения Ферро изложил в рукописи. На одном из диспутов Антонио Фиоре предложил учителю математики Жуану де Кои задачи на решение кубических уравнений, и тот обратился за помощью к своему другу Николо Тарталье. Тарталья сумел продвинуться в решении этих задач и публично заявил об этом. Фиоре, сочтя это заявление пустой похвальбой, вызвал Тарталью на поединок. " width="640"
0: Свой способ решения Ферро изложил в рукописи. На одном из диспутов Антонио Фиоре предложил учителю математики Жуану де Кои задачи на решение кубических уравнений, и тот обратился за помощью к своему другу Николо Тарталье. Тарталья сумел продвинуться в решении этих задач и публично заявил об этом. Фиоре, сочтя это заявление пустой похвальбой, вызвал Тарталью на поединок. " width="640"
 0. Это позволило ему решить все предложенные задачи. Чуть позже Тарталья нашёл способ для решения уравнений вида = ax + b, где a, b 0. Тарталья обнаружил также, что решение уравнения + b = ax позволяет решить уравнение =ax + b. " width="640"
0. Это позволило ему решить все предложенные задачи. Чуть позже Тарталья нашёл способ для решения уравнений вида = ax + b, где a, b 0. Тарталья обнаружил также, что решение уравнения + b = ax позволяет решить уравнение =ax + b. " width="640"