Картотека проблемных ситуаций по теме: «Величины. Единицы измерения величин»

Картотека проблемных ситуаций по теме: «Величины. Единицы измерения величин»

Длина

1. Миша и Саша выполняли задание: «Измерить длину школьного коридора».

Свои измерения они записали так: Саша – 16 шагов, Миша – 18 шагов.

Почему у мальчиков получились разные измерения? Как им помочь?

Учащиеся высказывают разные предположения.

1. Мартышка, Слоненок и Попугай измерили длину Удава. Свои измерения они записали так: Слоненок – 5 Мартышка – 50 Попугай – 500

Кто правильно выполнил задание?

Учащиеся высказывают разные предположения.

1. «Вова начертил полоски. Помоги ему сравнить их по длине.» .

- Как сравнить длины полосок, изображенных на рисунке? Можно

наложить их друг на друга? (Нет, сделать этого нельзя, они нарисованы.)

Учащиеся высказывают разные предположения.

На доске нарисованы две полоски, расположенные таким образом, чтобы нельзя было определить на глаз, какая полоска длиннее, какая короче.

- Сравните эти полоски по длине. Создалась проблемная ситуация: наложить нельзя, определить на глаз невозможно.

Учащиеся высказывают разные предположения.

- Задание было одно? (Да.)

- А как вы его выполнили? (По-разному.)

- Почему так получилось? Чего мы еще не знаем? (Полоски нельзя

наложить друг на друга, и они начерчены на доске, где нет клеточек.)

- Какой возникает вопрос? (Как сравнить полоски, которые нельзя

наложить друг на друга, сравнить на глаз или с помощью клеточек.)

Здесь мы видим, что учитель предложил учащимся проблемное задание. В результате его решения создалась проблемная ситуация. Затем с помощью побуждающего от проблемной ситуации диалога учитель подвел учащихся к формулированию проблемы.

1. На этапе постановки проблемы учитель может дать учащимся проблемное задание на сравнение:

1 век * 100 лет 100дм² * 1м² 100кг * 1ц

100 коп. * 1 руб. 1дм² * 100см² 1000м * 1км

Далее учитель задает вопросы:

- Смогли ли вы выполнить задание полностью?

- Меры каких величин вы сравнивали?

- Что означает запись 1км?

- Какая величина может быть измерена километрами?

Учащиеся высказывают разные предположения.

1. Во 2-м классе учащиеся знакомятся с новой единицей длины - с миллиметрами. Работу можно организовать следующим образом.

У учащихся на столах карточки, на которых начерчены два

отрезка друг под другом, один длиной 4см, а другой длиной 4см

5мм.

- Одинаковые ли отрезки?

- Какой отрезок длиннее?

- Какой короче?

Затем учитель предлагает найти длину отрезков и спрашивает:

- Смогли выполнить задание?

- В чем затруднение? (Длина верхнего отрезка 4см, а нижнего -

4см и остаток меньше 1см.)

- Можно ли измерить остаток? (Да.)

- Какие будут догадки?

- Какими единицами измерения длины его можно измерить?

Учащиеся выдвигают несколько гипотез, затем происходит

их проверка. Некоторые учащиеся знают единицу измерения длины – миллиметр.

Масса

1. На столе учителя стоят две одинаковые по цвету и форме коробки, но одна коробка пустая, а в другую положен какой-то тяжелый предмет.

- Сравните эти коробки. (Они одинаковые по цвету, по форме.)

- Есть ли отличие у этих коробок? (Нет.)

И все-таки учитель отмечает: различие между ними существует. Учащиеся столкнулись с проблемной ситуацией. Учитель

побуждает их к формулированию проблемы.

- Какой возникает вопрос? (Чем отличаются эти коробки?)

На этапе поиска решения проблемы диалог можно построить следующим образом:

- Какие есть предположения?

Учащиеся высказывают свои догадки. У некоторых возникает желание рассмотреть коробки поближе, взять их в руки. Взяв

в руки коробки, учащиеся обнаруживают, что одна коробка тяжелее другой.

1. Учитель предлагает ученикам две книги, которые очень незначительно отличаются по массе.

- Какая книга легче, какая – тяжелее?

Мнения учащихся расходятся.

- Задание было одно?

- А сколько мнений?

- Какой возникает вопрос?

Учитель побуждает учащихся сформулировать проблему.

Далее идет поиск решения это проблемы.

1. Учащимся предлагается задание сравнить массу дыни и массу пакета риса. Создалась проблемная ситуация.

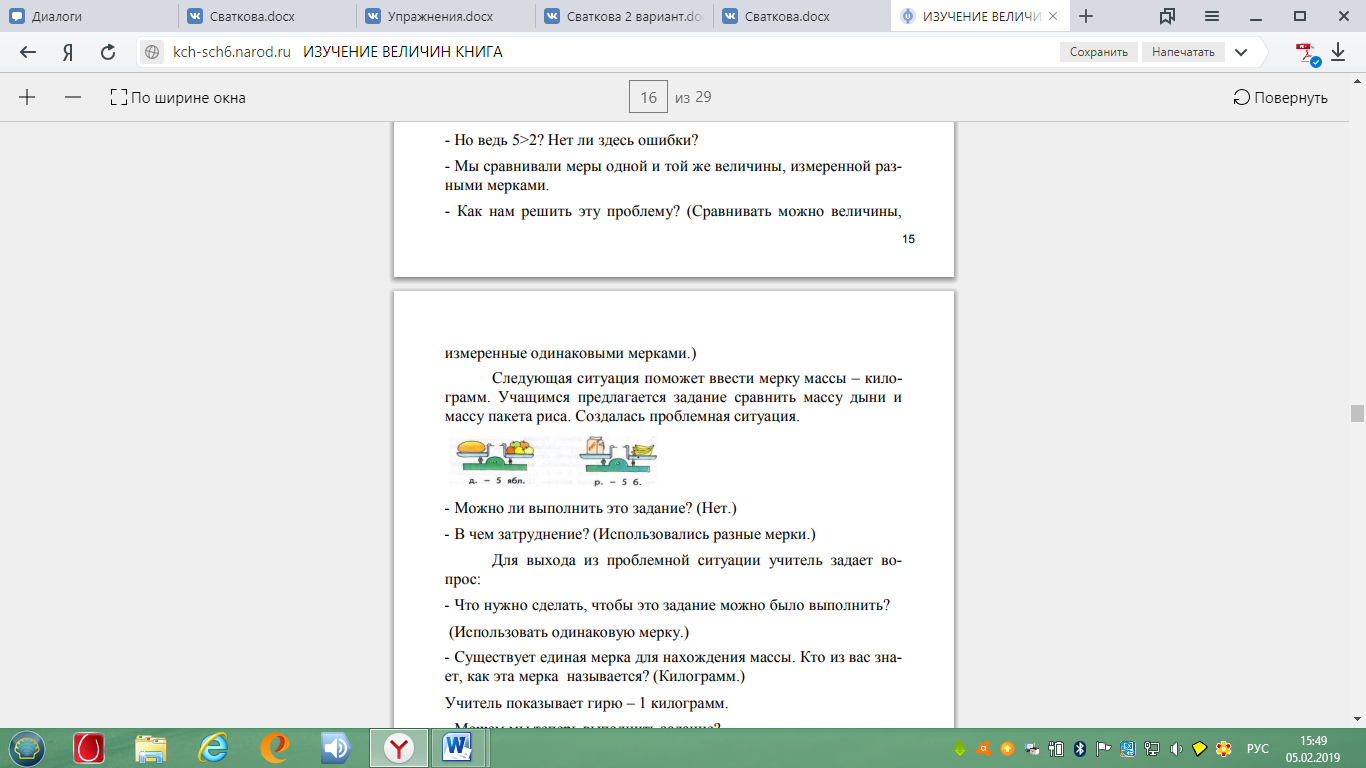
- Можно ли выполнить это задание? (Нет.)

- В чем затруднение? (Использовались разные мерки.)

Для выхода из проблемной ситуации учитель задает вопрос:

- Что нужно сделать, чтобы это задание можно было выполнить?

(Использовать одинаковую мерку.)

1. Учащимся предлагается задача: «Рассчитайте массу зерна на заводе, зная, что масса одного мешка – 50кг. Чему равна масса двух мешков? Трех?»

Учащиеся легко выполняют это задание.

- В день завод перерабатывает 1000 мешков. Сколько зерна он переработает за 1 день? (50000 кг зерна.)

- А теперь найдите, сколько зерна он переработает за месяц?

- Смогли выполнить задание?

- В чем затруднение?

- Чем это задание не похоже на предыдущее? (Получаются очень

большие числа.)

- Какой вы можете предложить выход из этой ситуации? (Нужна

более крупная мерка.)

Емкость

1. Предлагаются два сосуда с водой. Один узкий, другой широкий. Уровень воды в обоих сосудах одинаков. Кроме этого, на столе учителя два стаканчика различной емкости (обозначим их №1 и №2).

- Выясните с помощью мерки №1, в каком сосуде воды больше.

- Сколько мерок поместилось в широком сосуде? (7.)

- Сколько мерок поместилось в узком сосуде? (5.)

- Какой можно сделать вывод? (75. Значит, в широком сосуде

воды больше, чем в узком сосуде.)

- Выясните с помощью мерки №2, в каком сосуде воды больше.

- Сколько мерок поместилось в широком сосуде? (4.)

- Сколько мерок поместилось в узком сосуде? (2.)

- Какой можно сделать вывод? (42. Значит, в широком сосуде

воды больше.)

- Это свойство сосудов? (Да.)

- Кто знает, как называется это свойство? (Емкость.)

- Над какой темой мы сегодня будем работать? (Емкость.)

1. На столе учителя два сосуда: один широкий, другой узкий. В одном и другом налита вода. Уровень воды в узком сосуде выше, чем в широком сосуде. Учитель задает вопрос:

- В каком сосуде воды больше?

Мнения детей расходятся.

- Вопрос был один?

- А сколько мнений?

- Так чего мы еще не знаем, какой возникает вопрос?

Далее идет поиск решения проблемы.

Время

1. Детям предлагается прослушать две мелодии. Одна, из них длится 1 минуту, а другая мелодия - 55 секунд. После прослушивания детям задается вопрос:

- Какая мелодия длилась дольше?

Учитель создал проблемную ситуацию. Учащиеся затрудняются ответить.

- Вы можете выполнить задание?

- В чем затруднение?

Для выхода из проблемной ситуации учитель спрашивает:

- Как же нам узнать, какая мелодия длилась дольше? Какие есть

гипотезы?

Учащиеся выдвигают свои гипотезы и проверяют их. Если

во время работы учащиеся затрудняются с выбором правильной

гипотезы, то учитель предлагает:

- Во время прослушивания мелодии сосчитайте, сколько раз будет

двигаться стрелка на часах.

В процессе этой работы дети выясняют, что при прослушивании первой мелодии стрелка двигалась 60 раз и прошла полный

круг, т.е. мелодия длилась одну минуту. Вторая мелодия длилась

меньше, т.к. пока она звучала, стрелка двигалась 55 раз.

1. При знакомстве с веком, учащимся предлагается выполнить задание: Катя и Саша записали все известные им единицы измерения. На какие группы их можно разбить?

Литр, секунда, минута, дециметр, квадратный метр, месяц, час,

миллиметр, метр, сутки, килограмм, неделя, год, век.

- Назовите все известные вам элементы множеств «Единицы времени», «Единицы длины», «Единицы емкости», «Единицы массы», «Единицы площади».

- Все ли меры времени, записанные здесь, вам знакомы?

- Знаете ли вы, сколько лет длится век?

- Какие промежутки времени измеряют веками?

- Какой можно сделать вывод?

Площадь

1. Учащимся предлагается сравнить два квадрата и ответить

на вопрос:

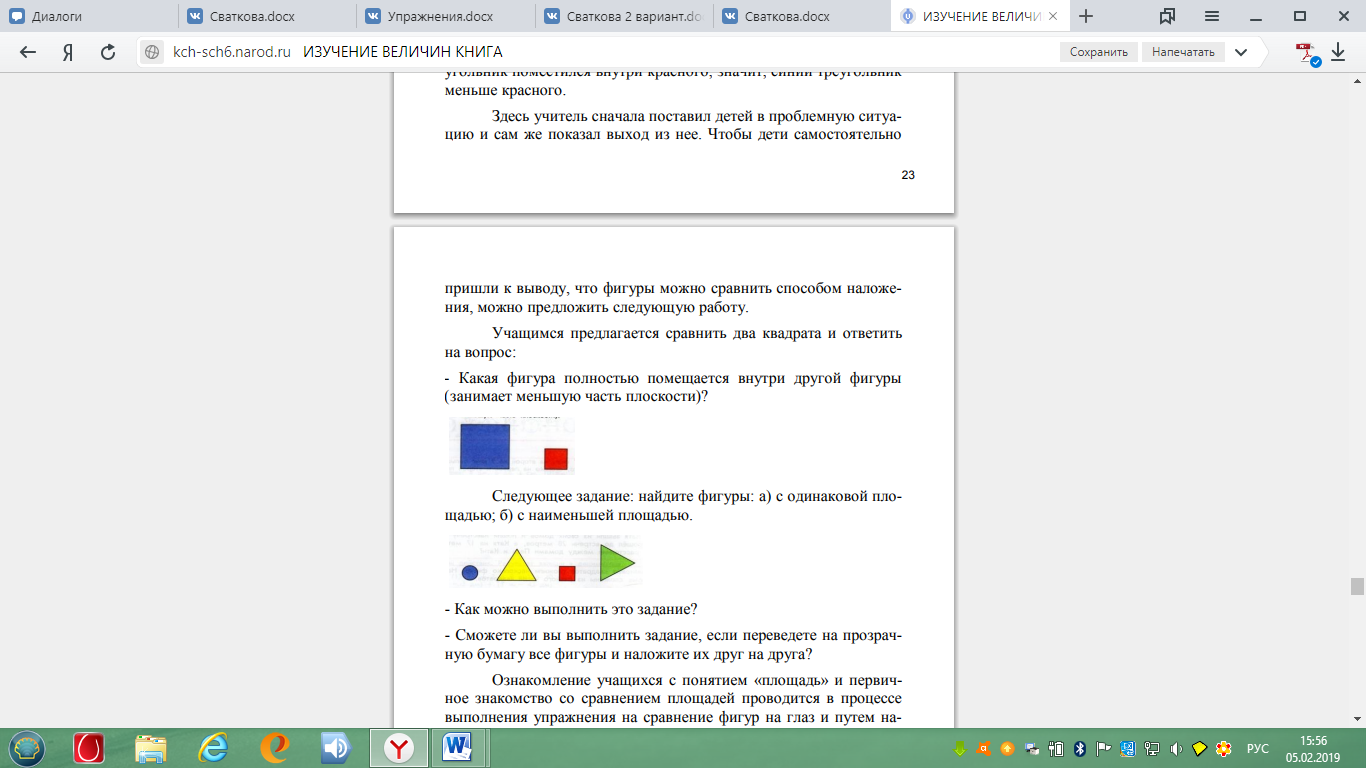
- Какая фигура полностью помещается внутри другой фигуры

(занимает меньшую часть плоскости)?

Следующее задание: найдите фигуры:

а) с одинаковой площадью; б) с наименьшей площадью.

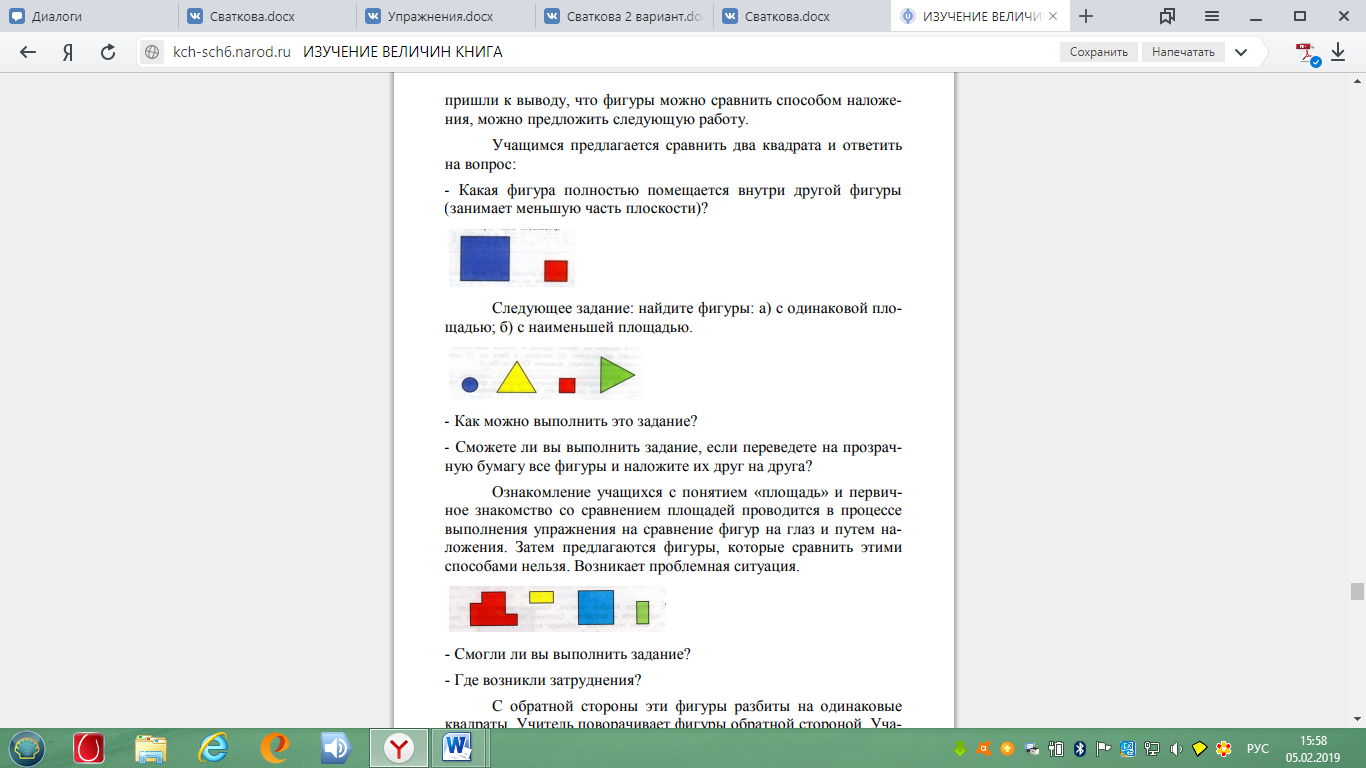
- Как можно выполнить это задание?

- Сможете ли вы выполнить задание?

1. По требованиям в учебном кабинете на одного учащегося должно быть не менее 3 кв. м.

Сколько учащихся могут находиться в учебном кабинете?

Что нужно знать, чтобы ответить на этот вопрос?

Узнай, сколько учеников могут находиться на уроке в вашем классе?

Литература

1. Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. учеб. заведений. -2-е изд., испр. - М.: Издательский центр «Академия»,1998.

2. Клименченко Д. Величины и их измерения // Начальная школа. - 1990.- №6.

3. Мельникова Е.Л. Проблемный урок, или Как открывать знания с учениками: Пособие для учителя. - М.: Просвещение, 2002.

4. Овчинникова М.В. Методика изучения темы «Величины» на уроках математики в начальных классах. Методические рекомендации для студентов факультета «Начальное обучение. Дошкольное воспитание.» - Ялта: ЦОП «Надежда», 2000.

5. «Школа 2100». Образовательная программа и пути ее реализации. //Под научной редакцией А.А. Леонтьева. Выпуск 3. - М.: Баласс, 1999.