Кинематика дифференциальных и планетарных механизмов

Дифференциальные механизмы

Дифференциальные механизмы имеют зубчатые колёса с подви осями (рис.6.5).

Зубчатое колесо 1 наз центр колесом, колесо 2, имеющ подв ось, – сателлитом, а звеноH, несущее сателлит, – водилом. Число ст подвиж механизма нах по фле Чебышева

W= 3n-2p₁-p₂=,

здесь n=3 – чло подв звеньев (колёса 1 и 2 водило H),

В данном мех=ме 2 нез закона движения, т.е. 2 звеньям м задать произв законы движ, тогда звено 2 б двигаться по опред закону.

Кинематика автомобильного дифференциала

При пом дифференц мех-ма (рис.6.6) в авто осущ передача вращат движения от двигателя к ведущим колёсам. При повороте дифференц мех-м распредел мощности меж ведущими колёсами так, чтобы их обороты согласовывались с усл движения.

Дифференц мех-м состоит из центрконич колёс 3 и 4, конич колеса – сателлита 5 и водила 2. Водило вып в виде конич колеса и передача вращения водилуосущ от карданного вала 1 при пом обычной конической передачи 1 – 2. На осн (6.2):

(6.4 (6.4) связыв обороты водила n₂ и об левого и правого колёс. Число обо n₂ явлизв. Если машина движется прямолин то к (6.4) доб n₃=n₄. При повороте к раве (6.4) доб:(6.5)Рав(6.4) и (6.5) позв получить определённреш и найти n₃ и n₄ 

Рис.6.6

Планетарные механизмы

Если у дифференц механизма центр колесо 1 сделать неподв и тем самым отнять 1 ст подвижн, то м получить зубчатый механизм с 1ст подвижности (рис.6.7).

Зубчатые мех со ст подвижности , у кот геом оси нек колёс перемещается, наз планетарными механизмами.

Найдём передаточное отн. Рассм планетарный мех-м как частн сл дифференц механизма и полагая ,м применить ф=лу (6.3). Получим:

=.Обр передаточное отн,

где  -передат отн от вала любого колеса n к валу водила H.След,

или  (6.6)

Отм, что к ф-ле (6.6) под цифрой 1 обозн неподв колесо. Это н учитывать и корректировать формулу при реш задач.

Кинематика дифференциальных и планетарных механизмов.

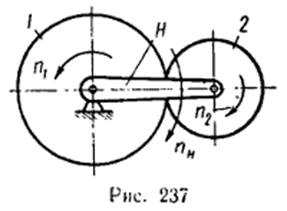
Планетарными наз передачи, в кот оси одного или неск колес закр в подвиж звене – водиле. Любая планетарная передача сост из 3 групп эл. 1я гр – центральные колеса (колеса, распол на неподв осях), 2я гр – сателлиты (колеса, распол на подв звене – водиле) и 3я группа – водила. На рис. 237 п схема передачи, сост из центрального колеса 1, сателлита 2 и водила H.

В общем сл центр колесо и водило м получвращ от 2 источн независимо др от др. Такая передача имеет 2 ст свободы и наз дифференциальной.

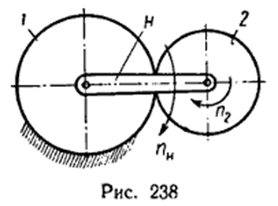
Если закрепить центр колесо, то получ передача с 1 стсв – движ м перед либо от водила к сателлиту, либо от сателлита к водилу – такая передача наз простой планетарной (рис. 238).

Сателлиты планетарных передач совер сложное вращдвижДвиж сателлитов отн Земли (отннепод с-мы к-т) склад из вращ их вместе с водилом – перенос дви и вращения их вокр осей, закреп в водиле, – относит движения.

Движение механизма относительно стойки

Движение механизма относительно водила

В движении звеньев отн водила угл скорости звеньев=угл скоростям в движ отн стойки – угл скорость водила. Если в движ отн стойки ось зубч колеса 2 под, то в движении отн водила оси обоих зубчатых колес непод. Поэтому к движ отн водила м применить осн теорему зацепления. т е м запис выр-ф-лу Виллиса для планетарных механизмов

Дифференц мех=мы не имеют постоянпередаточнотн. Передатотн м опр, ис метод обращён движения (метод Виллиса). Для этого дифф мех-му придаём допугл скорость= угл скор водила , но напр противоп. Это не измотн движения звеньев, абс же скорости б другими.

Такой дифф мех-м наз преобразованным, для кот справотн:(6.2)

полагая , м примен ф-лу (6.3). Получим:=.

Обратное передатотн,где  - передаточнотн от вала любого колеса n к валу водила H. След,или  (6.6)

Если в дифф механизме n зубчатых колёс:= (6.3)

Пример расчета

В планетарном механизме шестерня 1 рад R неподв, а кривошип ОА, вращвокрнепод оси, прох через тОперпендпл-ти рис, приводит в движ свободно насаж на конец А шестерню 2 рад r. Для указ на рис полож мех=ма найти скорости и ускор т А и В, если для соотвмо времени извабс вел угл скорости и углускорения кривошипа .

Исхданные R=0.6м r=0.4 м α=60 град ω_ОА=1 с^-1 ε_ОА=1 с^-2

1. Кривошип ОА совершвращ движение вокруг неподв оси, прох через т Оперпендплти рис. Опр скорость и ускор т А кривошипа, кот одноврпринадл и под шестерне 2.

Абс величина скорости т А . Для зад полож.
Вектор скор  напрперпенд ОА (рад вра) в напрвращ, на рис. 1 дуг стрелкой .

Ускор т Апредстразлож на касательную и нормальную составляющие
. (3), (4).
Для заданного положения
, (6). (7)
Касательнускор () напр по касат к этой ок (перпенд ОА) в стор, указ дуг стрел .

Величина ускорения т А

2. Шестерня 2 совершплоскопаралдвиж. Учит, что шест 2 катится без скольж по неподв шестерне 1, мцс (т )подв шестерни б нахо в точке соприкосн 2 шестерен (рис. 1)., зная вел скорости одной из точек и положмцс под шестерни, м опр вел её мгн угл скорости (ω₂) п, (7)где расст . . Для задан положения  .

Шестерня 2 в указ полож движется замедленно. Это следует из сопоставлнаправл векторов и  (направл в противоп сто). След, угловое ускор шест2 (ε₂) напр в сторону, противопнапр угловой скорости ω₂, что усл показано на рис.1 дуговой стрелкой ε₂.
Вел угл ускорения ε₂  ,
где  - вел углускор кривошипа ОА. Для зад полож.

Пр 2

Опр передаточное отн планетарного мех-маДано: z₁=100, z₂=99, =100, z₃=101.

передаточное отн здесь очень мало. Вал 1 вращ в 10 000 раз медл, чем вал водила. Для осущ такого малого перед отн при пом обычного зубчмехманбы сделать его многоступен, что потреб бы большого кол колес.но при таких передатотн планетарный мехм м надежно раб только в сторону уменьш числа оборотов ведом вала по ср с ведущим, т. е. м перед движ от водила к колесу. При передаче движ в сторону увел числа оборотов мех-м при таких передатотноблоч низким к. п. д. и даже м б самотормозящим, т. е. не м даже двигаться. Поэтому при оч малых передат отношениях планетарные передачи применя только в маломощных мех-мах, раб в течение небольших промежутков времени (напр, в приборах дистанционного управления).