| Мотивация к уроку (5 мин.) | Учитель проводит мотивационную беседу, готовит учащихся к постановке целей урока. Вы приехали в "Орленок" и уже на второй день вас переписывают в школу. По полученным данным, учеников распределяют по классам и перед завучами школы, ставится сложная задача. Она состоит в составлении расписания. Это расписание не только должно исходить из количества и состава класса, но и из желаний и возможностей учителей преподающих у этих классов. Сегодня мы поговорим с Вами о науке, разрешающей такие вопросы и задачи. Тема урока: "Комбинаторика"
Сегодня на уроке перед нами ставятся следующие задачи: 1. Познакомиться с понятием "Комбинаторика". 2. Научиться решать элементарные задачи из этого раздела математики.
Из истории: С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы. Еще с давних пор дипломаты, стремясь к тайне переписки, изобретали сложные шифры, а секретные службы других государств пытались эти шифры разгадать. Стали применять шифры, основанные на комбинаторных принципах, например, на различных перестановках букв с использованием ключевых слов и т. д. Многие ученые проводили исследования по комбинаторике. И только в 1666 г. была опубликована работа Готфрида Вильгельма Лейбница «Об искусстве комбинаторики». С этого момента комбинаторику рассматривают как самостоятельный раздел математики. Задача, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. Область математики, в которой изучаются комбинаторные задачи, называются комбинаторикой. И сегодня мы научимся находить возможные комбинации для решения элементарных комбинаторных задач и рассмотрим сферы их применения. | На экран монитора выводится первый слайд с темой урока. |
| Изучение нового материала (20 мин) | Речь пойдет о возможных вариантах решения элементарных задач комбинаторики основанных на трех простейших способах решения поставленных задач.
Способ первый - перебор. Перед учениками ставится задача - из группы теннисистов, в которую входят 4 человека - Антонов, Григорьев, Сергеев и Федоров, тренер выделяет двоих для участия в соревнованиях пар. Сколько существует вариантов выбора таких пар.
Вопрос ко всем ученикам. Когда удобен данный способ?
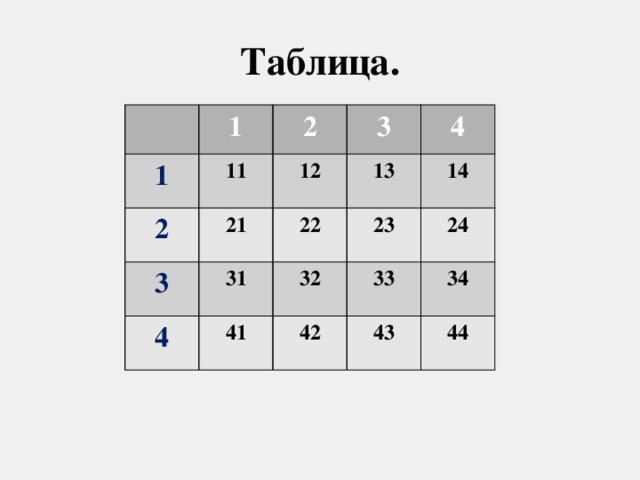
Хорошо, тогда пробуем еще один способ. Его основная цель составление таблицы возможных вариантов. Например: сколько можно составить двухзначных чисел из следующих цифр: 1, 2, 3, 4.
А что если я перед Вами поставлю условие, что цифры не должны повторяться??? То сколько тогда будет вариантов???
А когда удобен этот способ?
Правильно, ведь если нужно выбирать из трех или более элементов, то таблицу не составить, или же придется создать таблицу трехмерную, которую составить для обычного ученик - это серьезная проблема.
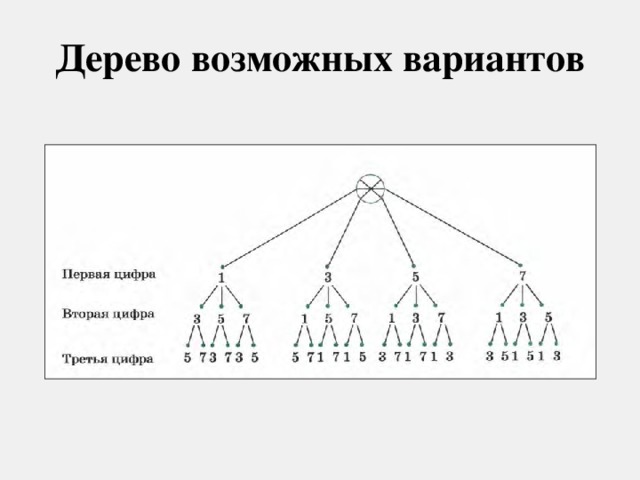
Есть еще один неплохой способ, именуемый, дерево возможных вариантов. Например - сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7, при условии, что цифры е повторяются.
Но и у этого способа есть слабое место? Как вы думаете?
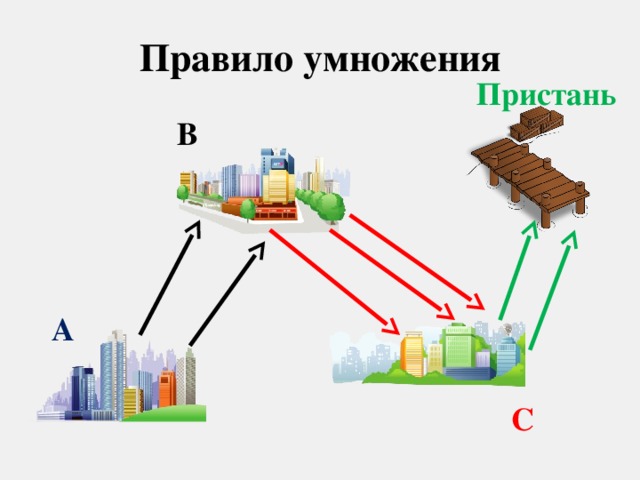
Рассмотрим следующую задачу: Из города А в город В ведут две дороги, из города В в город С - три дороги, из города С до пристани - две дороги. Туристы хотят проехать через города В и С к пристани. Сколькими способами они могут выбрать маршрут. | Учащимся рассказывается о примерах элементарных задач, изучаемых в комбинаторике и о способах их решения.
На экран выводится слайд 4, если есть ученики знающие ответ. они объясняют своими словами, как решать задачу, а затем учитель рассказывает о способе перебора остальным ученика. Если же таковых учеников нет, то учитель полностью объясняет способ перебора всевозможных вариантов на примере представленной задачи.
Правильный ответ: если количество элементов (участников), не очень большое количество (например от двух до пяти).
Детям демонстрируется слайд 5. В нем с помощью таблицы составлены все варианты двухзначных чисел из представленных четырех цифр. Правильный ответ будет 16.
Ученики должны исключить из таблицы варианты с одинаковыми цифрами. В ответе должно быть 12.
Правильный ответ ученика: если в задаче нужно составить всевозможные пары сочетаний или всевозможные варианты с двумя элементами.
Детям демонстрируется 6 слайд, с более сложным решением. В нем рассказывается еще об одном способе решения, дерево возможных вариантов (учитель подробно рассказывает о варианте решения.
Правильный ответ ученика - количество возможных вариантов. ведь если элементов будет больше 10, все способы считать придется долго!
Детям демонстрируется слайд 7. В данном способе используется комбинаторное правило умножения. (Учитель подробно излагает способ решения задачи). |
| Первичное закрепление (5 мин) | Нами рассмотрены возможные варианты решения простейших комбинаторных задач. Давайте теперь вы сами попробуете решить одну (все ученики уже заранее поделены на три группы). У меня в университете, преподаватель, ведущий предмет теория вероятностей, рассказывая про комбинаторику приводил такую жизненную ситуацию: "Однажды у нас дома произошла проблема с электричеством. Чтобы исправить неполадки, нужен был срочно электрик". Мой преподаватель знал, что он живет в соседнем доме. Подойдя к соседнему дому он увидел, что на двери установлен старый кодовый замок. Тут ему, как он рассказывал и понадобились навыки комбинаторики. Он знал, что эти кодовые замки трехзначные и для их открытия необходимо было перебрать все трехзначные комбинации. Начинал он с самого младшего числа и далее по старшинству . Как он утверждал - на каждую комбинацию у него уходило по две секунды, а открыл дверь он через дев минуты. Так какой же был код на двери?
| Детям демонстрируется слайд 8. И каждой группе ставится цель - решить эту задачу. Один ученик группы подходит к учителю с ответом. Если ответ правильный, ученику выдаются три номера. Первая группа, давшая правильный ответ получает карточку с номерами 714721726. Вторая группа - получает карточку с номерами 715722727. Третья группа - получает карточку с номерами 716723728. |
| Проверка знаний (7 мин) | Я много рассказал вам о комбинаторных задачах и о способах решения простейших задач. Но вот о истории становления этой науки я вам почти ничего не рассказал. Дело в том, что я немного позабыл о том, что хотел вам рассказать. Я специально дал вам листки с номерами. Это номера задач из учебника, которые вы должны решить. Ответы этих задач расположенных в порядке возрастания, дают нам код необходимый для открытия этих сундуков. (Детям демонстрируется программа с сундуками, которые необходимо открыть, введя в поле код, необходимую комбинацию(ответы задач)). Открыв эти сундуки, мы получим анаграмму из букв, которую нужно будет решить. Полученные слова помогут мне восстановить, то о чем из истории комбинаторики я хотел Вам рассказать.
"Китай" - Первое упоминание о вопросах, близких к комбинаторным, встречается в китайских рукописях, относящихся к 12-13 веку до нашей эры. В этих книгах писалось, что все в мире является сочетанием двух начал - мужского и женского со следующими элементами - земля, горы, вода, ветер, гроза, огонь, облака и небо. В этих же рукописях описано придание о императоре Ию, который увидел на берегу реки черепаху, на панцире которой был изображен рисунок из белых и черных кружков. (Детям демонстрируется слайд 9, рассказывается о магическом квадрате). "Игра" - значительный толчок к развитию комбинаторики дали азартные игры, существовавшие еще в глубокой древности, получившие распространение после крестовых походов. Наибольшее распространение получила игра в кости. А самая знаменитая игра - это конечно же покер. "Компьютер" - в эпоху компьютеров, комбинаторика приобретает самую важную роль, ведь комбинации в компьютерах встречаются везде.
| Учащиеся решают поставленные задачи. Группа с карточкой 714721726 должна получить ответ 83612. Введя этот код в необходимую программу ученикам открываются буквы слова "Компьютер". Аналогично для карточки 715722727, код - 1013230 и открываются буквы слова "Китай". Для третьей группы с карточкой 716723728, код - 1228180 и открываются буквы слова "Игра".
По мере угадывания слов, детям рассказываются факты из истории комбинаторики.
|