10 класс
Геометрия
Урок № 55
Тема: Усечённая пирамида. Площади поверхности усеченной пирамиды
Тип: урок изучения нового материала.
Цель: сформировать представление об усечённой пирамиде и её площади.
Задачи:
Образовательная:
изучить теоретический материал по теме «Усечённая пирамида»;
Разобрать и доказать теорему о площади поверхности усечённой пирамиды.
Развивающая:
Развитие навыки доказательства теорем;
Развитие самостоятельности и логического мышления.
Воспитательная:
Воспитывать интерес к геометрии;
Увеличение степени дисциплинированности и организованности на уроке;
Воспитывать внимательность и умение работать как самостоятельно, так и в коллективе.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга. Выявляются отсутствующие на уроке.
II. Проверка домашнего задания
Учитель берёт у 4–5 человек тетрадь для проверки выполнения домашнего задания.
III. Актуализация знаний учащихся
1. Фронтальный опрос
– Что называется пирамидой?
– Что называется правильной пирамидой?
– Что называется площадью боковой поверхности пирамиды?
– Что называется площадью полной поверхности пирамиды?
– Что называется трапецией?
– Что называется равнобедренной трапецией?
– Что называется прямоугольной трапецией?
– Как найти площадь трапеции?





2. Устное решение задач
Задача 1.
В С Дано: АВСD – трапеция;
BAD = 45
BC = 6 см
АD = 8 см
Найти: S – ?
А h1 h1 D
Решение:
h = 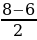 = 1 (см).
= 1 (см).
h = h1 tg45 = 1 (см).
h = h1 = 1 (см).
S = 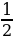 (8+6) 1= 7 (см2).
(8+6) 1= 7 (см2).
Ответ: S = 7 см2.
Задача 2.
В 4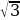 С Дано: АВСD – трапеция;
С Дано: АВСD – трапеция;


АВСЕ – квадрат;
ВС = 4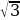 см, CDE = 30
см, CDE = 30
Найти: АD – ?
А Е D
Решение:
АЕ = 4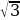 см
см
АЕ = ВС = СЕ = 4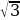 см;
см;
ЕD = 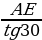 =
= 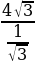 = 12
= 12
AD = (4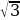 + 12) cм.
+ 12) cм.
IV. Постановка темы и целей урока
–Ребята, тема, которую нам сегодня предстоит разобрать, звучит так: «Усечённая пирамида. Площади поверхности усеченной пирамиды». Сегодня вам предстоит узнать, что это такое и разобрать теорему.
V. Изучение нового материала
Прошу ученика изобразить на доске произвольную пирамиду РА1А2…Ап.
Учитель говорит:
– Возьмём произвольную пирамиду РА1А2…Ап и проведём секущую плоскость , параллельно плоскости ɑ основания пирамиды и пересекающую боковые рёбра в точках В1,В2,…Вп. Плоскость разбивает пирамиду на два многогранника. Многогранник, гранями которого является п-угольники А1,А2,…Ап и В1,В2,…Вп (нижнее и верхнее основания), расположенные в параллельных плоскостях, и п-четырёхугольников А1А2В2В1, А2А3В3В2, … АпА1В1Вп (боковые грани), называется усечённой пирамидой.
Отрезки А1В1, А2В2, … АпВп называются боковыми рёбрами усечённой пирамиды. Усечённую пирамиду с основаниями А1,А2,…Ап и В1,В2,…Вп обозначают так:
А1А2…Ап В1В2…Вп. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды.
– Ребята, откройте учебник на странице 64. Посмотрите на рисунок 76.
– Назовите верхнее и нижнее основания, боковые грани и рёбра усечённой пирамиды, высоту усечённой пирамиды.
– Ребята, докажите, что боковая грань усечённой пирамиды – трапеция? (А1А2В1В2 – трапеция (А1В1 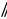 А2В2).)
А2В2).)
– Говорят, что усечённая пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию. Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции. Высоты этих трапеций называются апофемами. Встаёт вопрос: как найти сумму площадей её боковых граней? Площадью боковой поверхности усечённой пирамиды называется сумма площадей её боковых граней.
Sбок. = 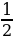 (р1+ р2) h,
(р1+ р2) h,
где р1 и р2 – периметры оснований;
h – апофема.
VI. Решение задач. Закрепление изученного материала/
1) Учитель возле доски решает №268
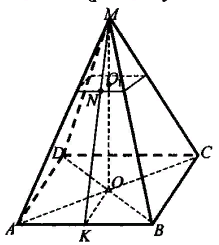
 Дано:
Дано:
MABCD – правильная пирамида,
А1В1С1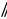 АВС,
АВС, 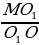 =
= 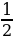 ,
,
NK – апофема, NK = 4 дм,
Sус.пир. = 186 дм2.
Найти: 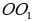 – ?
– ?
Решение: Рассмотрим МКО. Т.к. N1O1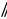 KO,
KO,
то 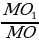 =
= 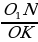 , значит, стороны
, значит, стороны 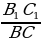 =
= 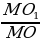 .
.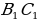 = 1 : 3.
= 1 : 3.
Пусть В1С1 = x, ВС = 3х. Имеем Sбок. = 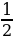 (4х+ 12х) 4. Sосн. = х2+ 9х2 = 10х2
(4х+ 12х) 4. Sосн. = х2+ 9х2 = 10х2
Sполн. = 10х2 + 32 = 186
5х2 + 16х – 93 = 0
D = 256 + 1860 = 2116,
т.к. D 0, то 2 решения.
х1 = 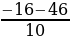 = – 6,2 – не удовлетворяет условию задачи, не может быть
= – 6,2 – не удовлетворяет условию задачи, не может быть
х2 = 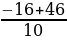 = 3
= 3
В1С1 = 3 (см), ВС = 9 (см), NO = 1,5 (см), OK = 4,5 (см). KF = OK – NO1 = 3.
Из KNF по теореме Пифагора NF = ОО1 = 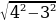 =
= 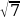 (дм).
(дм).
Ответ: 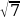 дм.
дм.
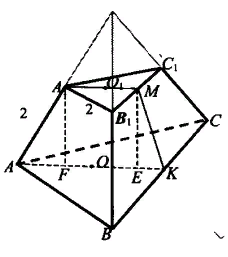
2) Ученик решает возле доски № 269
Дано:
ABCА1В1С1 – усечённая пирамида,
А1В1=В1С1=А1С1 = 2 см;
АВ = ВС = АС = 4 см; АА1 = 2см.
Найти: 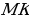 – ?
– ?
А1F1 – ?
Решение: Пусть О и О1 – центры оснований ирамиды.
1) Из АВС имеем: АВ = R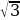 , R = AO.
, R = AO.
AO = 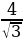 дм, ОК =
дм, ОК = 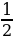 АО =
АО = 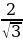 дм.
дм.
2) Из А1В1С1 находим А1О = 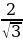 дм, О1М =
дм, О1М = 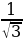 дм.
дм.
3) ЕК = ОК – ОЕ
ОЕ = О1М, остюда ЕК = 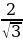 –
– 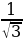 =
= 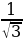 дм.
дм.
4) АА1F имеем: FA = AO – FO, FO = А1O, AF = 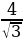 –
– 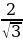 =
= 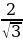 дм.
дм.
А1F = 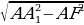 =
= 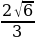 дм.
дм.
5) Из МЕК имеем: МК = 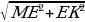 =
= 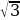 дм.
дм.
Ответ: 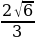 дм,
дм,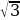 дм.
дм.
VII. Рефлексия учебной деятельности
– Что такое усечённая пирамида?
– Что такое апофема?
– Кому что осталось непонятым?
VIII. Подведение итогов урока
__________________________________________________________________________
Домашнее задание
Учитель раздаёт каточки с домашнем заданием.
| Фамилия, имя _____________________________________________
Дата «___» ______________ 20 __ г. Домашняя работа Пройдите тест: 
Ответы: 1 – __, 2 – __, 3 – __, 4 – __, 5 – __, 6 – __.
|












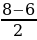 = 1 (см).
= 1 (см).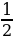 (8+6) 1= 7 (см2).
(8+6) 1= 7 (см2).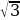 С Дано: АВСD – трапеция;
С Дано: АВСD – трапеция; 

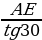 =
= 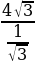 = 12
= 12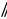 А2В2).)
А2В2).) 
 Дано:
Дано: 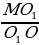 =
= 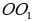 – ?
– ?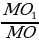 =
= 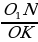 , значит, стороны
, значит, стороны 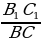 =
= 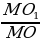 .
.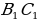 = 1 : 3.
= 1 : 3. 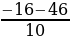 = – 6,2 – не удовлетворяет условию задачи, не может быть
= – 6,2 – не удовлетворяет условию задачи, не может быть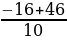 = 3
= 3 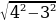 =
= 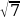 (дм).
(дм).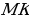 – ?
– ?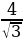 дм, ОК =
дм, ОК = 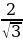 дм.
дм. 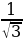 дм.
дм. 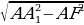 =
= 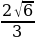 дм.
дм. 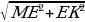 =
= 










