Урок по математике
«ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД».
Тип урока: урок изучения нового материала.
Цель: Ознакомление с многогранниками: тетраэдром и параллелепипедом. Формирование познавательных, регулятивных, коммуникативных УУД.
Воспитание внимания, наблюдательности, умения слушать, умения читать, конспектировать и понимать текст учебника, развитие самостоятельного, творческого, логического мышления.
Задачи: 1. Повторить и обобщить теоретический материал по теме «Параллельность прямых и плоскостей»
2. Ввести понятие многогранника, тетраэдра, параллелепипеда, рассмотреть их элементы, свойства.
3. Изображать рассматриваемые объекты на плоскости. Решить задачи на применение полученных знаний.
План урока.
Организационный момент. 3 мин.
Актуализация знаний. 18 мин.
Изучение нового материала. 40 мин.
Решение задач. 25 мин.
Подведение итогов, задание домашнего задания. 4 мин.
Ход занятия.
Организационный момент.
Приветствие преподавателя Проверка готовности к занятию. Организация внимания. Сегодня мы начинаем изучение новой темы, название которой вы скажете сами, отгадав ребус, представленный на слайде.
Какое слово зашифровано в этом ребусе?
Многогранник. Параллелепипед. Тетраэдр. Сообщение темы урока самими обучающимися.
Актуализация ранее приобретенных знаний.
1).3 обучающихся работают у доски по пройденному материалу. Доказательство признака параллельности прямой и плоскости, свойства параллельных плоскостей и решение задачи 63 (б). Остальные работают по карточкам.
Установить соответствие
Две прямые в пространстве называются параллельными, если они Если одна из двух параллельных прямых пересекает плоскость, то и Две прямые называются скрещивающимися, если они Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она Прямая и плоскость называются параллельными, если они Две плоскости называются параллельными, если они Если прямая и плоскость имеют бесконечное множество общих точек, то прямая | а) не лежит в одной плоскости
б) не имеют общих точек
в) лежит в плоскости
г) не пересекаются
д) лежат в одной плоскости и не пересекаются
е) параллельны
ж) параллельна данной плоскости
з) другая прямая пересекает эту плоскость |
Самопроверка (ответы на слайде презентации) , выставление в листок самооценки баллов за проделанную работу.
Отвечают обучающиеся , которые работали у доски, остальные слушают. Выставляются оценки.
2) Задание по вариантам.
I ВАРИАНТ.
Найти ошибку, переставить прямоугольники:
Две прямые


Лежат в одной плоскости.
Не лежат в одной плоскости


Скрещиваются
Пересекаются.
II ВАРИАНТ.
Найти ошибку, переставить прямоугольники:
Две плоскости.



Имеют одну общую точку.
Имеют множество общих точек
Не имеют общих точек.



Плоскости параллельны
Плоскости пересекаются
Плоскости совпадают
Проверка, выставление оценок в листок самооценки.
Изучение нового материала.
1) Преподаватель знакомит обучающихся с понятием многогранник. Слайды презентации.
2) Презентацию «Тетраэдр. Параллелепипед» подготовили 2 обучающихся (им заранее было дано творческое задание). Остальные слушают.
3) Работа по изучению и конспектированию теоретического материала по вариантам.
Вариант 1
а). Прочитайте п.12, абзац 3, стр.24
б). Запишите определение тетраэдра и выпишите его элементы
Противоположные рёбра тетраэдра - ?
в). Как изобразить тетраэдр на плоскости?
г). Заполните таблицу.
| Многогранник | Количество рёбер | Количество вершин | Количество
граней | Вид грани |
| Тетраэдр (tetra – четыре, hedra – грань) |
|
|
|
|
Вариант 2
а). Прочитайте п.13, абзац 1 – 3 до слов: Две грани параллелепипеда…., стр.25
б). Запишите определение параллелепипеда и выпишите его элементы
в). Как изобразить параллелепипед на плоскости?
г). Заполните таблицу.
| Многогранник | Количество рёбер | Количество вершин | Количество
граней | Вид грани |
| Параллелепипед от греч. parallelos - параллельный и epipedon - плоскость) |
|
|
|
|
Проверка фронтально. На доске заполнить таблицу и вывести формулу Эйлера.
Выставление оценки в листок самооценки знаний.
4).Работа с учебником стр.25
Задание 1. Запишите определения (учебник, п.13, абзац 3 и 4, стр.25):
а) смежные грани -
б) противоположные грани -
в) боковые грани-
г) противоположные вершины -
д) диагональ параллелепипеда -
Задание 2. Начертите параллелепипед и проведите в нём диагонали.
Задание 3. Выпишите свойства параллелепипеда:
Противоположные грани параллелепипеда… ?
Диагонали параллелепипеда…?
Поменялись тетрадями, проверили друг у друга и выставили оценки в листок самооценки знаний, который сдали преподавателю.
IV. Решение задач.
Открываем учебник на странице 29.
№ 68 выполняем устно по готовому чертежу.
№ 67 письменно. Читаем задачу. Один обучающийся выходит к доске,
остальные работают в тетрадях
Дано: DABC – тетраэдр,  ADB=54,
ADB=54,  BDC=72,
BDC=72,  CDA=90, DA=20 см, BD=18 см, CD=21 см.
CDA=90, DA=20 см, BD=18 см, CD=21 см.
Найти: а) ребра основания АВС; 
б) S всех бок. сторон.
Решение: а) 


б) SADC=1/2 *AD*DС= ½*20*21=210;
SВDC= ½*18*21*sin72=179.95;
SВDА=1/2 *BD* AD= ½*18*20* sin54=145,62.
Ответ: а) АС=29, АВ=17,7, ВС=23,36.
б) SADC=210; SВDC =179.95; SВDА=145,62.
№70. С комментированием решаем. ДАНО: DABC тетраэдр.
AM=MB , AK=KC, AN=ND
Доказать, что (MNK)∣∣(BCD)

Решение.
MK ∣∣BC (свойство средней линии треугольника)
MN ∣∣BD (свойство средней линии треугольника)
MK∩MN
BC∩BD отсюда следует, что (MNK) ║ (BCD) по признаку параллельности двух плоскостей.
Страница 30, выполняем №76:
Дан параллелепипед ABCDA1B1C1D1. Докажите, что АС||A1C1 и BD∣∣B1D1.
Дано: ABCDA1B1C1D1 - параллелепипед.
Доказать, что АС||A1C1, BD∣∣B1D1
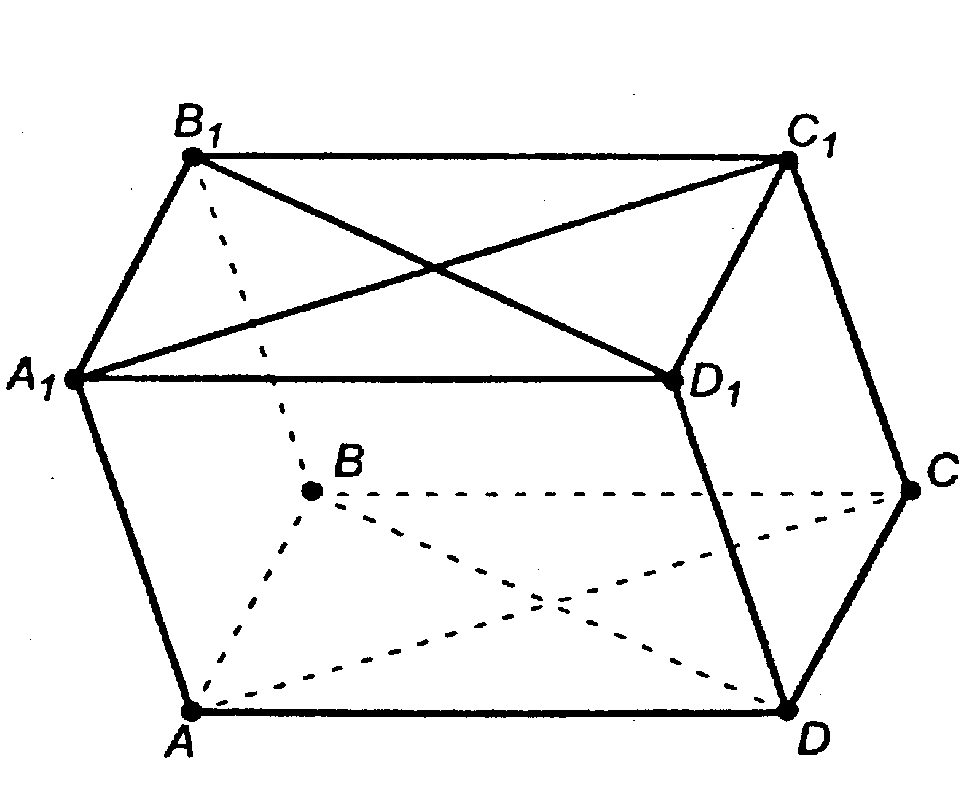
Док-во:1) Рассмотрим четырехугольник АА1С1С:
Т.к. АА1D1D - параллелограмм (по определению),= АА1|| D1 D.
Т. к. DD1С1С - параллелограмм (по определению),= D1 D || С1С.
Таким образом, АА1||С1С.
2) В силу свойств параллелепипеда АА1С1С - параллелограмм, отсюда А1С1 || AC.
3) Аналогично B1D1 D B - параллелограмм, поэтому B1D1 || BD.
Объявляются оценки обучающимся, работавшим у доски.
V. Подведение итогов. Рефлексия.
Сегодня на уроке мы познакомились с понятием тетраэдр, параллелепипед.
Что такое тетраэдр? Что такое параллелепипед? Назовите свойства
параллелепипеда.
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
сегодня я узнал…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал, что…
я приобрел…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
урок дал мне для жизни…
мне захотелось…
Домашнее задание. Выучить пункт 12,13.
Доказать свойства параллелепипеда. Выполнить презентацию
«Тетраэдр и параллелепипед».
















 ADB=54,
ADB=54, 















