ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЛУГАНСКОЙ НАРОДНОЙ РЕСПУБЛИКИ
«КРАСНОЛУЧСКИЙ УЧЕБНО-ВОСПИТАТЕЛЬНЫЙ КОМПЛЕКС № 6
«СОЗВЕЗДИЕ»
Методическая разработка
урока геометрии
11 класс
по теме «Объемы пространственных фигур»
Автор:
Мороз Лидия Васильевна,
специалист высшей
квалификационной категории,
учитель математики
г. Красный Луч
Введение
Как известно, важное значение в процессе обучения математике имеет понимание школьниками практической значимости того или иного учебного материала. В данной методической разработке подобраны задачи практического содержания в которых вычисляется объём пространственных фигур.
Актуальность использования задач с практическим содержанием в курсе геометрии не вызывает сомнения, так как условия естественного развития личности ребёнка наиболее полно реализуются в случае, когда обучение раскрывает взаимосвязь геометрии не только с другими науками, но и с жизнью. Данная разработка показывает, что математические абстракции возникают из практики, из задач, поставленных реальной действительностью.
Задачи с практическим содержанием это средство мотивации изучения теоретического материала, так как именно на примере практических задач можно показать необходимость знания той или иной теоремы для решения проблем возникающих перед человеком в повседневной жизни и профессиональной деятельности.
Основная часть
Цель: формировать навыки практического применения теоретических знаний по теме «Объёмы пространственных фигур» для решения задач.
Задачи
образовательные:
– показать практическую значимость данной темы в жизни человека;
– формировать навыки решения практических задач;
– формировать умения правильного построения чертежей;
развивающие:
– развивать умение правильно пользоваться формулами для решения задач;
– развивать умение самостоятельно мыслить;
– развивать абстрактное мышление и пространственное воображение;
воспитательные:
– воспитывать интерес к предмету математика, любознательность;
– воспитывать взаимовыручку, взаимоподдержку.
План урока
| № | Этап урока | Формы, методы используемых педагогических технологий | Требования к результатам обучения |
|
| 1 | Организационный момент | Работа над эпиграфом урока | Концентрация внимания учащихся. Положительный эмоциональный настрой |
|
| 2 | Актуализация опорных знаний | Самопроверка выполнения домашнего задания по готовому решению (индивидуальная работа, наглядно-иллюстративный метод). Работа с моделями геометрических тел (групповая работа, наглядно-иллюстра-тивный метод). Фронтальный опрос теоретических знаний (репродуктивный метод). | Повторение ранее изученного материала, формирование адекватной оценки своих достижений, осуществление выделения необходимой информации; структурирование знаний |
|
| 3 | Постановка проблемы и цели урока | Проблемные методы | Формулировка темы урока и целей урока |
|
| 4 | Формирова-ние знаний, умений, навыков | Групповые технологии, межпредметные связи с историей, экологией, физикой, проблемные вопросы, решение практико-ориентированных задач, решение задач по готовым чертежам «Аукцион идей». При решении задач используется проблемно-поисковый метод. | Умение применять формулы объемов геометрических тел и свойства объёмов при решении практических задач, умение создавать математические модели реальных объектов. Умение работать в группе, собирать и анализировать информацию, слушать, обсуждать вопросы при коллективной работе, высказывать свои суждения, выслушивать других, опровергать их доводы или соглашаться с ними, аргументировать свои доказательства, учиться правильно распределять время. Презентовать результат своей работы. |
|
|
| Физкультминутка | Здоровьесберегаю-щая технология | Отдых, релаксация, снятие напряженности. |
|
| 5. | Домашнее задание | Уровневая дифференциация, творческая работа | Закрепление изученного, развитие творческого потенциала |
|
| 6. | Рефлексия | Работа с листами рефлексии. Минутка хвастовства. | Осознание содержания пройденного, оценка эффективности собственной работы на уроке |
|
Конспект урока
1. Организационный момент
Учитель: Здравствуйте! Присаживайтесь!
Посмотрите, пожалуйста, друг на друга, улыбнитесь!
Посмотрите на меня, улыбнитесь!
Пожелаем успеха друг другу и начнем урок!
Сегодня на уроке вы будете работать в группах. (Группы сформированы заранее.) Для совместной работы нужна взаимовыручка, взаимоподдержка, умение слушать и слышать друг друга, принять точку зрения другого. Надеюсь, ваша совместная работа сегодня будет именно такой.
Французский философ ученый Блез Паскаль утверждал: «Величие человека в его способности мыслить». (Слайд 2)

Мы отправимся в увлекательный мир геометрии, который откроет вам некоторые тайны, связанные с телами вращения, ведь геометрия полна приключений. Помните, что за каждой задачей скрывается приключение.
2. Актуализация знаний, умений, навыков
а) проверка домашнего задания
Учитель: Обратите внимание на слайд и выполните самопроверку. (слайд 3)

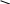 У кого есть вопросы по решению задачи? (Вопросов нет)
У кого есть вопросы по решению задачи? (Вопросов нет)
А что пропущено при решении задачи? (Вычисления, даны только ответы)
При решении задачи должно быть все вычисления.
б) геометрическая разминка
Какую тему мы изучаем? (Объёмы тел)
Объёмы каких тел изучили? (Объём конуса, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, усеченного конуса, усеченной пирамиды).
Вспомним формулы объёмов тел. На ваших столах стоят фигуры геометрических тел и лежат карточки, на которых написаны части формул. Вам необходимо восстановить формулу, прочитать ее, выбрать соответствующую модель тела и показать на ней основные элементы. (Обучающиеся закрепляют формулы на доске, показывают модель геометрического тела и основные элементы)
(Приложение 1)
Для успешной работы на уроке нам нужно вспомнить свойства объёмов.
(Равные тела имеют равные объёмы. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел)
На каком уроке вы еще сталкивались с нахождением объема? (на физике)
Вспомните формулу плотности вещества. (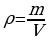 )
)
Значит, m=? (m= ρV)
Как зависит объем цилиндра и конуса от радиуса основания и высоты? (Прямо пропорционально высоте и квадрату радиуса)
Чему равно отношение соответственных сторон подобных треугольников? (Коэффициенту подобия к)
В каких единицах измеряется объём? (В кубических единицах)
А еще? (В литрах)
Напоминаю! 1 литр=1 дм3
Заполните листы рефлексии.
3. Постановка целей и задач урока.
Учитель. Мы с вами повторили формулы объёмов пространственных тел, свойства объемов и единицы их измерения. Как вы думаете, чем мы будем заниматься на уроке? (Учиться решать задачи, используя данные формулы)
Правильно. Будем учиться решать задачи в том числе и практического содержания, а также задачи ГИА.
Открываем тетради, записываем число, классная работа, «Решение задач по теме «Объёмы пространственных фигур».
4. Формирование знаний, умений, навыков
Учитель. А теперь переходим к основному этапу работы в группах. Сегодня у нас работают группы «Изготовители мороженого», «Экологи», «Историки». Представители групп подготовили исторические справки, с которыми нас познакомят. Каждая группа получает задачу, которую нужно решить, записать решение в тетради, оформить чертеж и решение задачи на доске. После оформления на доске группа готова к отчету. Выступает один представитель группы, объясняет решение задачи. Остальные обучающиеся слушают, задают вопросы, оценивают ответ, предлагают свое решение, затем записывают решение в тетрадях.
Задание группе «Изготовители мороженого»:
Мороженое знали и любили еще во времена Киевской Руси. Особое место отводили лакомству из измельченного замороженного молока или сливок. А ведь это и есть прототип современного мороженого пломбир! Многие считают, что история мороженого пломбир пошла именно от славян. Так как упоминание рецепта впервые встречается на территории Киевской Руси. Хотя официально его придумали французы, назвав лакомство в честь местечка Плобьерле Беем.
Дана модель конуса. Выполнить необходимые измерения и определить вес мороженого, которое можно поместить в данный рожок, если плотность пломбира 1,1 г/см3 .
Р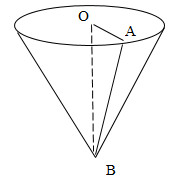 ешение
ешение
Измеряем длину окружности основания конуса, используя нить. Длина окружности равна 19 см.
Используя линейку измеряем образующую конуса. Образующая конуса АВ = 10 см. Из
формулы l = 2πr находим радиус. r=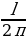 ,
,
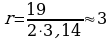 (см), ОА = r ≈ 3 см.
(см), ОА = r ≈ 3 см.
Из ∆АОВ (∠О = 90) по теореме Пифагора
АВ2 = АО2 + ВО2, тогда ВО = 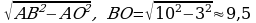 (см).
(см).
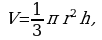 где h = ВО, r = ОА.
где h = ВО, r = ОА.
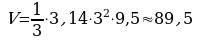 (см3)
(см3)
m = ρV, m=1,1.89,5 ≈ 98,5 (г)
Ответ: 98,5 г
Вопросы обучающихся команде «Изготовители мороженого».
Как можно измерить диаметр основания конуса? (Штангенциркулем или линейкой, но для этого нужно точно знать расположение центра круга)
Задание группе «Историки»:
Египетские пирамиды – древнейшее и вместе с тем единственное, сохранившееся до наших дней, чудо света. Пирамида Хеопса – самая большая пирамида. Она была самым большим сооружением всего мира, пока в 1889 году не уступила первенство Эйфелевой башне.
Основанием пирамиды служит квадрат со стороной 230 м, угол наклона боковой грани к плоскости основания равен 50 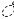 . Найдите объём самой высокой Египетской пирамиды, если основание высоты находится в центре квадрата.
. Найдите объём самой высокой Египетской пирамиды, если основание высоты находится в центре квадрата.
Решение
П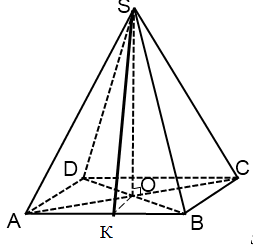 усть SABCD – данная пирамида, в основании которой лежит квадрат ABCD, AB = 230 м, точка О – центр квадрата. SО – высота пирамиды.
усть SABCD – данная пирамида, в основании которой лежит квадрат ABCD, AB = 230 м, точка О – центр квадрата. SО – высота пирамиды.
Проведем ОК АВ, тогда по теореме о трех перпендикулярах SК АВ.
∠SКО – линейный угол двугранного угла SABD, ∠SКО=50 ̊ .
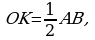 ОК = 115 м.
ОК = 115 м.
Из ∆SОK (∠О = = 90) SO=OK tg∠SКО, SO = 115۰1,2 ≈ 138 (м).
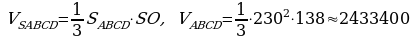 (м3).
(м3).
Ответ: 2433400 м3
Вопросы обучающихся группе «Историки»
Почему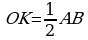 ? (Перпендикуляр, проведенный к середине стороны квадрата, равен ее половине)
? (Перпендикуляр, проведенный к середине стороны квадрата, равен ее половине)
Задание группе «Экологи»:
29 мая на площадке электростанции Норильско-Таймырской энергетической компании из-за проседания опор лопнул резервуар. Из него вытекло дизельное топливо. 15 тысяч тонн попало в реки Далдыкан и Амбарная, еще 6 тысяч – в грунт. Амбарная впадает в огромное озеро Пясино. Дальше – Карское море. Эта авария стала первой аварией такого крупного масштаба в заполярной Арктике. Минприроды считает, что восстановление экосистемы в районе аварии займет не менее 10 лет.
У бензовоза, ехавшего вдоль берега океана, заглох мотор. Если через 12 минут шоферу не удастся уехать, поднимающийся прилив утащит машину в пучину моря, и 10 тонн бензина попадет в океан. На помощь приходят рабочие грузовика, на котором оказалось 50 пустых бочек. Диаметр основания каждой бочки – 0,5 м, высота – 1 м. Бензин можно заливать в бочки через шланг со скоростью 900 л/мин. Если опорожнить цистерну, еще один грузовик сможет отбуксировать бензовоз в безопасное место. Хватит ли бочек, чтобы перелить бензин? Успеют ли рабочие это сделать?
Решение
10 тонн бензина имеют объём 10000 л.
Бочка имеет форму цилиндра. Ее объем V=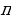 r2h, где h = 1 м, r = d:2,
r2h, где h = 1 м, r = d:2,
r = 0,5:2 = 0,25 (м).V = 196,25 л.
Находим количество бочек 10000:196,25 ≈ 50,9 ≈ 51
Чтобы перелить полностью бензин, бочек не хватит.
Но этого достаточно для отбуксировки бензовоза.
Найдем время, необходимое для опорожнения цистерны
1000:900 = 11,11 (мин). Рабочие успеют опорожнить цистерну.
Ответ. Бочек не хватит. Рабочие успеют опорожнить цистерну.
Вопросы обучающихся группе «Экологи»
Какие знания применяли при решении этой задачи? (Свойство объемов)
Пока представители групп готовятся к отчету, остальные обучающиеся по готовому чертежу определяют объёмы фигур.
Задачи, которые мы сейчас решим, предлагались на ЕГЭ по математике (базовый уровень).
 Слайд 4
Слайд 4
(Ответ: 2000 см3 )
 Слайд 5
Слайд 5
Ответ: 600 см3. В каких единицах должен быть ответ? (В литрах. Ответ:0,6 л)
При решении задач нужно внимательно читать условие. Это залог успешного решения задачи.
Слайд 6

(Ответ: 21 см3)
Какие знания применяли при решении этой задачи? (Свойство объемов)
Физкльтминутка
Один обучающийся показывает движения, остальные повторяют или импровизируют. Звучит ритмичная музыка (1 минута)
Выступления с отчетами.
Вы успешно справились с полученными заданиями. Смогли ответить на вопросы одноклассников. Вы почувствовали себя «великими людьми»? (Да)
А теперь я вам предлагаю провести «Аукцион идей». По готовым чертежам определить, какие величины можно найти. Задания взяты из ГИА.
Слайд 7 Вариант 2. Задание 2.4.
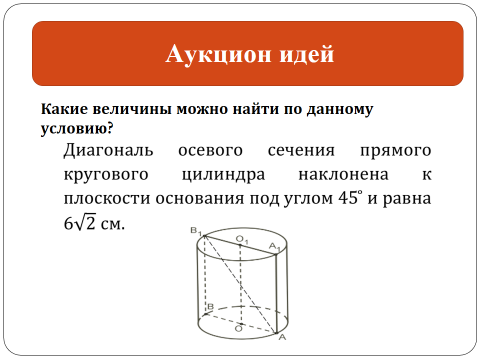
(углы ВАВ1, АВ1В, АВ1А1, А1АВ1, высоту, радиус, доказать, что сечение – квадрат, объем, площадь основания, площадь боковой поверхности, площадь полной поверхности)
Слайд 8 Вариант 8. Задание 2.4.

(углы сечения В и С, образующую АВ, высоту АО, радиус ОВ, объем, площадь основания, площадь сечения, определить вид сечения (проходит через высоту), площадь боковой поверхности, площадь полной поверхности).
5. Домашнее задание. Слайд 9

6. Рефлексия
Заполните листы рефлексии.
А теперь минутка хвастовства
Вы сегодня хорошо работали. Я думаю, что для вас домашнее задание не покажется трудным, так как подобные задачи мы разобрали на уроке.
Слайд 10
Методические рекомендации по проведению урока
Данный урок можно проводить после изучения теоретического материала об объемах пространственных тел, а также при итоговом повторении, подготовке обучающихся к ГИА. Может быть использован как занятия математического кружка.
Обучающимся предлагается подготовить мини-сообщения об истории возникновения мороженого, египетских пирамидах, экологической катастрофе.
Перед уроком происходит деление ребят на группы. Ребята, как правило, уже знают правила работы в группе.
При решении практических задач нужно обратить внимание обучающихся на то, что создаются математические модели реальных жизненных ситуаций, с помощью геометрического чертежа они визуализируются для того, чтобы увидеть где применяются полученные при изучении геометрии теоретические сведения. При решении задач необходимо обращать внимание на внимательное изучение условия задания. Очень много ошибок допускают обучающиеся по невнимательности. Учитель постоянно мотивирует детей на изучение геометрии. Показывает, что изучаемый материал возник из реальных потребностей людей.
Материально-техническое обеспечение урока.
Ноутбук, мультимедийный проектор, модели геометрических тел, штангенциркуль, линейка, нить, таблицы Брадиса.
Список использованной литературы
Далингер В.А. Поисково-исследовательская деятельность учащихся по математике: учебное пособие. – Омск: Изд-во ОмГПУ. 2005. - 456 с.
Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций / базовый и углубл. уровни [Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.]. – 3-е изд. – М.: Просвещение, 2016. – 255 c.
Скопец З.А. Геометрические миниатюры/ З.А. Скопец. – М.: Просвещение. 1990. – 220 с.
Пухначев Ю.В. Математика без формул / Ю.В. Пухначев, Ю.П. Попов. – М.: Знание. 1979. – 158 с.
Семенов С.С. За страницами учебника геометрия / С.С. Семенов. – М.: Просвещение. 1999. – 340 с.
Приложения
Приложение 1
| 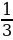 Sоснh Sоснh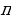 r2h r2h
|
| 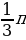 r2hSосн r2hSосн
|
| 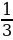 h(S+ S1+ h(S+ S1+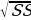 1) 1)
|
| 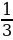 h(S+ S1+ h(S+ S1+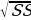 1) 1)
|
Лист рефлексии
| Моя деятельность | Справился сам | Справился с помощью | Не справился |
| Домашнее задание решение задачи |
|
|
|
| Повторение: формулы объемов |
|
|
|
| Повторение: свойства объемов |
|
|
|
| Повторение: элементы геометрических тел |
|
|
|
| Работа в группе |
|
|
|
| Решение задач по готовым чертежам |
|
|
|
| Задачи ГИА |
|
|
|
| Творческое задание |
|
|
|
| Оценка за урок |
|
|
|









 У кого есть вопросы по решению задачи? (Вопросов нет)
У кого есть вопросы по решению задачи? (Вопросов нет)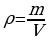 )
) ешение
ешение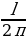 ,
,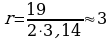 (см), ОА = r ≈ 3 см.
(см), ОА = r ≈ 3 см.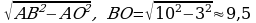 (см).
(см).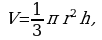 где h = ВО, r = ОА.
где h = ВО, r = ОА.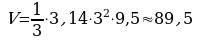 (см3)
(см3) . Найдите объём самой высокой Египетской пирамиды, если основание высоты находится в центре квадрата.
. Найдите объём самой высокой Египетской пирамиды, если основание высоты находится в центре квадрата. усть SABCD – данная пирамида, в основании которой лежит квадрат ABCD, AB = 230 м, точка О – центр квадрата. SО – высота пирамиды.
усть SABCD – данная пирамида, в основании которой лежит квадрат ABCD, AB = 230 м, точка О – центр квадрата. SО – высота пирамиды.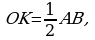 ОК = 115 м.
ОК = 115 м. 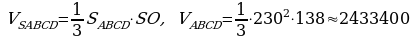 (м3).
(м3).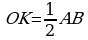 ? (Перпендикуляр, проведенный к середине стороны квадрата, равен ее половине)
? (Перпендикуляр, проведенный к середине стороны квадрата, равен ее половине)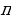 r2h, где h = 1 м, r = d:2,
r2h, где h = 1 м, r = d:2,  Слайд 4
Слайд 4 Слайд 5
Слайд 5




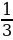 Sоснh
Sоснh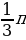 r2hSосн
r2hSосн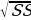 1)
1)









