Конспект урока: "Площадь фигур"

Проверил

Дата

Подпись

Отметка за конспект:

Отметка за урок:

11 ноября.

Классная работа.

Площадь

3 см

4 см 5 см

6460

1615

5*3=15

3*5=15

S = a х b

11 ноября.

Классная работа.

Площадь

27

8

17

32

3

3 см

4 см 5 см

6460

1615

5*3=15

3*5=15

S = a х b

Тема

«Площадь. Сравнение площадей фигур»

Цель урока

Организация деятельности детей по формированию и первичному усвоению знаний о площади, формированию умений сравнивать площади различными способами.

способами сравнения фигур: “на глаз”, путём наложения одной

фигуры на другую, с использованием подсчета квадратов

представление о площади фигур, познакомить с различными

способами сравнения фигур: “на глаз”, путём наложения одной

фигуры на другую, с использованием подсчета квадратов

Планируемые результаты

Коррекционные:

- коррекция речи;

- коррекция мышления.

Предметные:

- уметь использовать в речи термин  «площадь»;

- уметь находить площадь фигуры разными способами;

- применять правило порядка выполнения действий при вычислении значения выражения;

- развивать вычислительные  навыки и умения.

Личностные:

- овладение способностью самостоятельно оценивать свои результаты и оценивать действия своих одноклассников;

-осознание своих возможностей в учении;

-способность адекватно судить о причинах своего успеха или неуспеха.

Метапредметные:

- определять цель учебного задания, контролировать свои действия в процессе его выполнения;

- развивать способность обнаруживать и исправлять ошибки.

УУД:

Познавательные:

- обобщать (выделять ряд объектов по заданному признаку);

- делать выводы в результате совместной работы класса и учителя;

- проводить аналогии между изучаемым материалом и собственным опытом;

Регулятивные:

- принимать и сохранять учебную задачу, соответствующую этапу обучения;

- в сотрудничестве с учителем, классом находить несколько вариантов решения учебной задачи;

Коммуникативные:

- принимать участие в работе;

- договариваться и приходить к общему решению в совместной деятельности;

- адекватно использовать средства устного общения для решения коммуникативных задач.

Основные понятия

Площадь, сравнение площадей

Межпредметные связи

Русский язык, литературное чтение.

Ресурсы (оборудование):

- основные

- дополнительные

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Для учащихся: учебник математики для 3 класса

Моро, рабочая тетрадь, линейка, простой карандаш, геометрические

фигуры: квадраты белый 6х6 см, белый 4х4 см, круги белые,

прямоугольник 5х3.

Для учителя: геометрические фигуры: квадраты белый 6х6 см, белый

4х4 см, круги белые, прямоугольник 5х3.

Учебник М. И. Моро, «Математика» 3 класс, 1 часть; рабочая тетрадь. Интерактивная доска проектор, компьютер, линейка, простой карандаш. Геометрические фигуры: белые квадраты 6*6 см, 4*4 см, белые круги, прямоугольник 5*3 см.

Презентация, геометрические фигуры: белые квадраты 6*6 см, 4*4 см, белые круги, прямоугольник 5*3 см.

Организация пространства

Фронтальная работа, индивидуальная работа.

Технология проведения

Деятельность учителя

Деятельность учеников

1. Мотивация к учебной деятельности

1 мин

Здравствуйте, ребята! Меня зовут Ольга Станиславовна, я рада приветствовать вас на нашем уроке математики.

Прозвенел звонок весёлый.

Мы начать урок готовы.

Будем думать, рассуждать,

И друг другу помогать.

- Прочитайте слова на доске: «Всё познаётся в сравнении!» (слайд 1). Они и будут девизом нашего урока. Какая деятельность будет основной на уроке? (познавать и сравнивать)

- Верно! Если мы приложим достаточно усилий, то сможем изучить новую тему.

Проверяют готовность к уроку. Настраиваются на работу, садятся за парту.

2. Актуализация и фиксирование индивидуального затруднения в пробном действии

Устный счёт

5 мин

- Откройте тетради, запишите число и "Классная работа".

11 ноября.

Что вы скажете о числе 11? (двузначное)

- Какой сейчас идёт месяц? (ноябрь)

- Какой это месяц по счёту? (одиннадцатый)

- Что скажете о числе 15?(оно двузначное)

- Давайте сравним эти два числа.

15 больше 11. На сколько больше? (на 4)

- Вот мы и начали процесс сравнения на уроке математики. И вы видите, что математика очень тесно связана с жизнью.

- Поэтому продолжим работать.

- Отступите от последней записи две клетки вниз и две клетки от края тетради.

Я сейчас буду читать выражения. Вам нужно записать только ответы через клетку вниз.

Слушайте внимательно!

1. Увеличьте 9 в 3 раза (27).

2. Уменьшите 32 на 4 (8).

3. Сумма чисел 8 и 9 (17).

4. Разность 40 и 8 (32).

5. Найдите частное чисел 18 и 6 (3).

6. В большой коробке 16 карандашей, а в маленькой 8 карандашей.

Во сколько раз в большой коробке карандашей больше, чем в маленькой? (в 2 раза)

Взаимопроверка

- Поменяйтесь с соседом тетрадью. Возьмите в руку простой карандаш. Я буду читать правильные ответы.

Если у вас также, ставите знак «+», если другой ответ - знак «-».

Если у соседа нет ошибок, на полях карандашом поставьте оценку 5.

Если 1-2 ошибки, ставите оценку 4.

Если 3 ошибки - 3.

Если больше трёх минусов ничего не ставите.

Записывают в тетрадь число, классная работа.

Записывают ответы.

Выполняют взаимопроверку.

3. Этап выявления места и причины затруднений

7 мин

- Ребята, как вы думаете, для чего нам нужны знания таблиц умножения и деления, свойства геометрических фигур?

 – Знание таблиц умножения и деления, свойств геометрических фигур понадобится нам при изучении темы нашего урока.

Слайд 2.

         – Два брата близнеца, Филя и Киря, решили смастерить столики для кукольного домика.

Слайд 3.

Они выпилили столешницы прямоугольной формы. Филя вырезал столешницу со сторонами – 3 см и 8 см. Киря – 4 см и 6 см.

Слайд 4.

        После того, как мальчики выполнили эту работу, им стало интересно: а у кого столешница получилось больше?

        Слайд 5.

        Филя: «У меня! Потому что выше!»

        Киря: «У меня! Потому что шире!»

        Мальчики не смогли определить, чей же стол будет больше?

        Я предлагаю вам помочь справиться Филе и Кире с этой проблемой.

(Возможно, дети предложат свои варианты, например, найти периметр: если периметр больше, значит ли это, что столешница больше?)

Дети сходятся во мнении, что нужно обратиться за помощью к учителю.

Чтобы решать примеры, задачи, высчитывать периметр.

Выполняют вычисления.

Ответы детей.

4. Этап построение проекта выхода из создавшейся ситуации

3 мин

 – Чтобы узнать, чья столешница больше, нужно найти ПЛОЩАДЬ.

- Ребята, а вы слышали слово «Площадь»? Где оно вам встречалось?

Слайд 6,7.

- Скажите, вы уже догадались, какая будет тема нашего урока?

- Какую же цель мы поставим на сегодняшнем уроке?

- Закончите предложения:

Познакомиться с понятием …

… со способами сравнения фигур

- Отлично!

- Составим план работы:

Слайд 8, 9.

1. Узнать … (что такое площадь).

2. Научиться сравнивать … (площади фигур).

3. Закрепить умение … (сравнивать площади фигур различными способами).

Учащиеся говорят, что встречали данное слово в словосочетаниях:

Красная площадь, площадь 40- летия Победы, площадь квартиры, площадь спортивной площадки (площадь в центре города, строительная площадка, площадка во дворе для игр, спортивная площадка, лестничная площадка, площадь обоев, площадь стола, площадь футбольного поля, площадь поля, засеянного какими-либо культурами и др.).

- Площадь

- Площадь

- Познакомиться

Ответы детей.

5. Реализация построенного проекта

15 минут

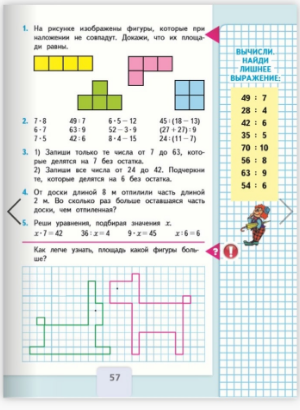
- Сегодня мы с вами рассмотрим слово ПЛОЩАДЬ с математической точки зрения. Это слово часто будет звучать сегодня на уроке. Запишите новое слово в тетрадь.

Словарная работа

Назовите орфограммы в слове “ Площадь”.

- Гласная после шипящих: сочетание ча-ща пиши с буквой а;

- Смягчающий мягкий знак, смягчает предшествующий согласный

звук, а сам звука не даёт.

-В математике принято обозначать данную величину латинской буквой S. Запишите в тетрадь.

Работа с геометрическим материалом

а) Возьмите квадраты. Покажите квадрат, который больше.

Как сравнивали?

Видно “ на глаз”.

Про такие фигуры говорят, что площадь большого квадрата больше

площади маленького квадрата.

Как ещё можно сравнить площади этих фигур?

Можно наложить одну на другую.

Наложите и сравните площади квадратов.

Маленький квадрат полностью вместился в большой, значит площадь большого квадрата больше площади маленького квадрата.

б) Возьмите круги. Сравните площади и покажите круг, площадь

которого меньше.

Площади кругов равны, так как при наложении круги полностью совпали. Понятие площади.

 – А что такое площадь? Как вы это понимаете?

        Слайд 10, 11.

 – В толковом словаре Владимира Даля: 

Площадь – это величина, которая указывает, сколько места занимает фигура на плоскости.

Как мы сравнивали площади фигур?

Физкультминутка

Вот Незнайкина зарядка.

Выполняйте по порядку.

Быстро встаньте, улыбнитесь,

Выше, выше потянитесь.

Ну-ка плечи распрямите,

Поднимите, опустите.

Влево, вправо повернулись,

Рук коленями коснулись.

Сели – встали,

Сели – встали,

Вы, надеюсь, не устали?

Надо вам свободно встать

И спокойнее дышать.

Единицы площади

а) Возьмите прямоугольник и белый квадрат.

Как удобнее сравнивать площади прямоугольника и квадрата “на

глаз” или наложением?

Дети пытаются сравнить площади фигур “на глаз” и наложением.

“На глаз” или наложением сравнить площади прямоугольника и

квадрата нельзя, фигуры разные по форме и ни одна полностью не

вмещается в другой.

Как же сравнить площади этих фигур?

Если правильного ответа не будет, учитель сам предлагает начертить

прямоугольник и квадрат в тетради.

а) Назовите общие свойства прямоугольника и квадрата.

Чем отличаются?

б). Вычерчивание прямоугольника и квадрата в тетради.

Измерьте сторону квадрата.

4 см

Начертите квадрат. Укажите на чертеже длину стороны квадрата.

Измерьте длину и ширинку прямоугольника.

5 см, 3 см

Начертите прямоугольник. Укажите длины сторон прямоугольника.

Как же сравнить площади этих фигур?

1. Если правильного ответа не будет, обратить внимание детей на то,

что, начертив фигуры в тетради, мы разбили их на одинаковые

фигуры меньшего размера – клетки тетради.

Можно посчитать клетки.

Посчитайте клетки, I вариант – квадрата, II вариант - прямоугольника.

- Сколько клеток поместилось в квадрате, в прямоугольнике?

Запишите числа и сравните их.

6460

Сравните площади квадрата и прямоугольника.

Площадь квадрата больше площади прямоугольника.

Большую площадь имеет та фигура, которая содержит большее число клеток.

2. Разобьём квадрат и прямоугольник на квадраты со стороной 1см.

Подсчитайте, сколько квадратов со стороной 1см поместилось в квадрате?

В прямоугольнике? Запишите числа и сравните их.

1615

Сравните площади фигур.

Площадь квадрата больше площади прямоугольника.

Результат сравнения площадей не зависит от выбора единиц

измерения.

3. Как удобнее подсчитать квадраты, на которые разбит прямоугольник?

1 способ: посчитать по порядку

2 способ: 3 ряда по 5 квадратов, 5 • 3 = 15

5 столбцов по 3 квадрата, 3 • 5 = 15

Какое предположение можем выдвинуть? Площадь прямоугольника и квадрата

находится произведением длины и ширины.

Запишите в тетрадь вычисления.

4. Подведём итог наших наблюдений. Так что же такое площадь?

Это количество квадратов, которое умещается в данной фигуре.

Если обозначить стороны буквами a, b, то получаем формулу: S = a х b

Запишите формулу в тетрадь.

Как можно сравнить площади фигур?

(“на глаз” и наложением друг

на друга)

Как можно вычислить площадь фигуры? Используя формулу.

Записывают слово Площадь в тетрадь.

- На глаз

- Наложить их друг на друга.

Выполняют, повторяя за учителем.

Ответы детей.

- “На глаз” и наложением друг на друга.

Ответы детей.

- 6460

- 1615

- Площадь прямоугольника и квадрата

находится произведением длины и ширины.

- Количество квадратов в фигуре.

- “На глаз” и наложением друг

на друга.

- Через ф-лу: S= a х b.

6. Первичное закрепление с проговариванием во внешней речи

5 мин

- Откройте учебник на стр.57 № 1 (устно).

- Прочитайте задание (1 ученик).

На рисунке изображены фигуры, которые при наложении не

совпадут. Докажите, что их площади равны.

- Кто скажет, какой способ мы здесь применим? Что нужно будет сделать?

( посчитать квадратики)

- Кто может доказать? (Все фигуры состоят из 4 квадратов одинаковой площади, значит, площади фигур равны.)

- А теперь посмотрите на эти фигуры. (Учитель показывает фигуры).

- Что вы заметили? (Квадраты разные по размеру.)

- Будут ли  площади фигур равны? Почему? (разная площадь)

- А как мы можем сравнить эти фигуры в таком случае? (на глаз)

- Молодцы!

- В каждом предложении есть главные члены.

- Посчитать квадраты.

- Все фигуры состоят из 4 квадратов одинаковой площади, значит, площади фигур равны.

- Квадраты разные по размеру.

- Нет, потому что у них разная площадь.

- «На глаз».

7.Самостоятельная работа с самопроверкой по эталону

5 мин

- Замечательно! Продолжаем урок.

-Давайте проверим, насколько хорошо вы усвоили сегодняшнюю тему урока.

- Перед вами на партах лежат карточки. Возьмите их. Вам необходимо разделить рисунок на три фигуры одинаковые по площади, и раскрасить их

разными карандашами.

Построй фигуру равную по площади данной, но другой формы.

- Хорошо. Сравните работу с доской (слайд 15).

- Все ли справились с заданием?

- У кого выполнено правильно?

- У кого ошибки?

- Молодцы. Справились с заданием.

Ответы детей.

8. Этап включения в систему знаний и повторений

2 мин

- Какую тему урока мы сегодня проходили?

- Какая была цель? Достигли её?

- Что такое площадь фигуры? (это то, сколько фигура занимает места на плоскости)

Отвечают на вопросы.

9.Рефлексия учебной деятельности на уроке

2 мин

Домашнее задание

- Итак, ребята, наш урок подходит к концу.

Вернёмся ещё раз к девизу «Всё познается в сравнении!» Вспомним наш план.

1. Узнать … (что такое площадь).

2. Научиться сравнивать … (площади фигур).

3. Закрепить умение … (сравнивать площади фигур различными способами).

На все ли пункты плана мы нашли ответы?

- В чём возникли трудности?

Откройте дневники, запишите домашнее задание: стр. 57 №5.

- На столе у вас лежат круги, закрасьте ту часть, которая соответствует вашей личной оценке за урок. Спасибо! (Приложение 1)

Отвечают на вопросы.

- Площадь

- Сравнивать площадь разных фигур.

- Да!

Ответы детей.

Записывают домашнее задание.

Оценивают свою деятельность на уроке.