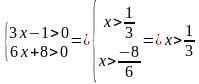Алгебра
10 класс
Урок № ____
Тема: Логарифмические уравнения
Цель урока: повторить понятие и свойства логарифма; изучить способы решения логарифмических уравнений и закрепить их при выполнении упражнений.
Задачи урока:
- обучающие: повторить определение и основные свойства логарифмов, уметь применять их при вычислении логарифмов и решении логарифмических уравнений;
-развивающие: развивать логическое мышление, память, внимание, культуру математической речи;
-воспитательные: воспитывать настойчивость, самостоятельность; прививать интерес к предмету.
Тип урока: формирование новых знаний.
Ход урока
Организационный момент
Проверка д/з
Формулирование целей и задач урока
Актуализация опорных знаний
1. Дайте определение логарифма.
2. От любого ли числа можно найти логарифм?
3. Какое число может стоять в основании логарифма?
4. Функция y=log0,8 x является возрастающей или убывающей? Почему?
5. Какие значения может принимать логарифмическая функция?
6. Какие логарифмы называют десятичными, натуральными?
7. Назовите основные свойства логарифмов.
8. Можно ли перейти от одного основания логарифма к другому? Как это сделать?
Изучение нового материала
Определение: Уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.
Простейшим примером логарифмического уравнения служит уравнение 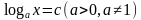 .
.
Способы решения логарифмических уравнений:
Решение уравнений на основании определения логарифма
Метод потенцирования
Уравнения, решаемые с помощью применения основного логарифмического тождества
Метод приведения логарифмов к одному и тому же основанию
Решение уравнений на основании определения логарифма.
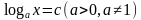 имеет решение
имеет решение 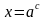 .
.
На основе определения логарифма решаются уравнения, в которых:
по данным основаниям и числу определяется логарифм,
по данному логарифму и основанию определяется число,
по данному числу и логарифму определяется основание.
| Пример 1 | Пример 2 | Пример 3 |
| 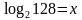
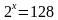
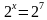
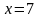
Ответ: 7 | 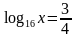
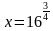
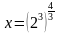
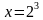
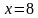
Ответ: 8 | 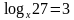
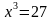
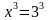
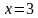
Ответ: 3 |
Метод потенцирования.
Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их т.е. 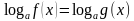 , то
, то 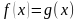 , при условии, что
, при условии, что 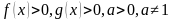 .
.
Пример: Решите уравнение 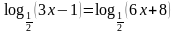
| 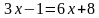
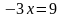
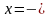 3 3
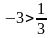 - неверно - неверно
Ответ: решений нет.
| ОДЗ: 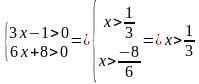
|
Уравнения, решаемые с помощью применения основного логарифмического тождества.
Пример: Решите уравнение
| 


 – не принадлежит ОДЗ – не принадлежит ОДЗ
 – принадлежит ОДЗ – принадлежит ОДЗ
Ответ: х=2
| ОДЗ:
|
Метод приведения логарифмов к одному и тому же основанию.
Пример: Решите уравнение 
| 



 – принадлежит ОДЗ – принадлежит ОДЗ
Ответ: x = 16.
| ОДЗ: x 0
|
Закрепление изученного материала
______________________________________________________________________________________________________________________
Домашнее задание
___________________________________________________________
Подведение итогов урока





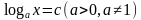 .
.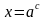 .
. 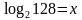
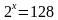
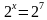
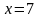
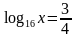
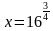
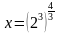
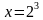
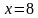
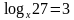
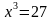
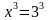
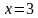
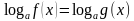 , то
, то 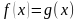 , при условии, что
, при условии, что 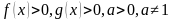 .
. 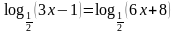
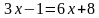
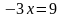
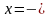 3
3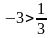 - неверно
- неверно