Конспект урока по геометрии, 7 класс, «Сумма углов треугольника».

Конспект урока по геометрии в 7 классе

Тема урока: «Сумма углов треугольника».

Тип урока: урок изучения нового материала.

Учебник: Геометрия 7-9 класс, Атанасян Л.С.

Учитель: Лобасова Анастасия Алексеевна.

Цель: формировать умение доказывать теорему о сумме углов треугольника, решать простейшие задачи по данной теме.

Ученик должен знать:

• Виды треугольников, понятие внешнего угла треугольника.

• Теорему о сумме углов треугольника.

• Теорему о внешнем угле треугольника.

• Теорему о соотношениях между углами и сторонами треугольника.

Ученик должен уметь:

• Уметь находить неизвестные внутренние углы треугольника.

• Уметь находить внутренний угол треугольника, смежный с внешним углом.

• Уметь определять существование треугольника с заданными сторонами и с заданными углами.

• Четко и аккуратно выполнять геометрические построения.

Планируемые результаты изучения темы:

Личностные: проявляют познавательный интерес к предмету.

Предметные: умеют осуществлять проверку выводов, положений, закономерностей; доказывать и применять при решении.

Метапредметные результаты изучения темы (универсальные учебные действия): познавательные: проводят сравнение, сериацию и классификацию по заданным критериям, умеют отвечать на поставленные вопросы; регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета сделанных ошибок, осмысливают ошибки и устраняют их; коммуникативные: считаются с разными мнениями и стремятся к координации различных позиций в сотрудничестве.

Ход урока.

1. Организационный момент

Данный урок предназначен для ознакомления с темой «Виды треугольников». При помощи него все желающие смогут получить представления о том, что представляет собой треугольник, какие существуют виды этой геометрической фигуры. Также учитель расскажет об одной из важнейших теорем – сумме углов треугольника.

2. Теорема о сумме углов треугольника

В этом уроке мы рас­смот­рим виды тре­уголь­ни­ков. Рас­смот­ре­ние видов тре­уголь­ни­ков ба­зи­ру­ет­ся на важ­ной тео­ре­ме о сумме углов тре­уголь­ни­ка.

Тео­ре­ма 1: Сумма углов тре­уголь­ни­ка равна  .

Дано: ∆АВС.

До­ка­зать: ∠1 + ∠2 + ∠3 = .

До­ка­за­тель­ство: Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

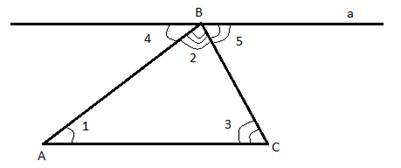
Рис. 1. Ри­су­нок к тео­ре­ме 1

Через точку В про­ве­дем пря­мую а, па­рал­лель­ную сто­роне АС. Такая пря­мая су­ще­ству­ет и яв­ля­ет­ся един­ствен­ной. ∠1 = ∠4 по свой­ству па­рал­лель­ных пря­мых и се­ку­щей АВ, по этому же свой­ству ∠3 = ∠5. ∠4 + ∠2 + ∠5 =  , а зна­чит, ∠1 + ∠2 + ∠3 = . Тео­ре­ма до­ка­за­на.

АВ = АС – бо­ко­вые сто­ро­ны. ВС – ос­но­ва­ние.

3. Теорема о внешнем угле треугольника

Перед тем как рас­смот­реть тео­ре­му о внеш­нем угле тре­уголь­ни­ка, сле­ду­ет ска­зать о внеш­нем угле. ∠4 (смеж­ный с ∠3) – внеш­ний угол ∆АВС.

Тео­ре­ма 2: Внеш­ний угол тре­уголь­ни­ка равен сумме двух углов тре­уголь­ни­ка, не смеж­ных с ним.

Дано: ∆АВС.

До­ка­зать: ∠4 =∠1 +∠2.

До­ка­за­тель­ство:  Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

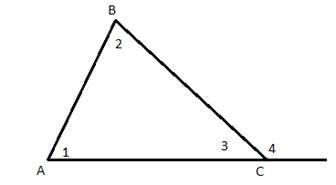
Рис. 2. Ри­су­нок к тео­ре­ме 2

Зна­чит, ∠4 = ∠1 + ∠2, что и тре­бо­ва­лось до­ка­зать.

1. Виды треугольников

Виды тре­уголь­ни­ков

1. Если в тре­уголь­ни­ке все углы ост­рые, то такой тре­уголь­ник на­зы­ва­ет­ся ост­ро­уголь­ным. 

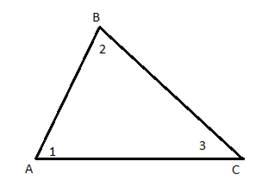
Рис. 3. Ост­ро­уголь­ный тре­уголь­ник

При­ме­ры: а. ∠1 = ∠2 = ∠3 = . Зна­чит, в сумме имеем  .

б.  ∠1 = , ∠2 = ∠3 = .

2. Если в тре­уголь­ни­ке есть угол, рав­ный  , то такой тре­уголь­ник на­зы­ва­ет­ся пря­мо­уголь­ным.

∠С = .

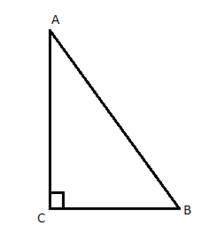
Рис. 4. Пря­мо­уголь­ный тре­уголь­ник

∠А + ∠В +  = .

∠А +∠В = – = . Зна­чит, ∠А и ∠В ост­рые. Таким об­ра­зом, в пря­мо­уголь­ном тре­уголь­ни­ке один угол  , два осталь­ные угла – ост­рые.

Для сто­рон пря­мо­уголь­но­го тре­уголь­ни­ка су­ще­ству­ют спе­ци­аль­ные на­зва­ния. Сто­ро­на, ле­жа­щая про­тив пря­мо­го угла, на­зы­ва­ет­ся ги­по­те­ну­зой, а дру­гие сто­ро­ны на­зы­ва­ют­ся ка­те­та­ми.

3. Если в тре­уголь­ни­ке один угол на­хо­дит­ся в пре­де­лах ( ; ), то такой тре­уголь­ник на­зы­ва­ет­ся ту­по­уголь­ным.

Рис. 5. Ту­по­уголь­ный тре­уголь­ник

∠А + ∠В = – ∠С. ∠А и ∠В – ост­рые.

При­мер 1: До­ка­жи­те, что в любом тре­уголь­ни­ке най­дет­ся хотя бы один угол, ве­ли­чи­на ко­то­ро­го не мень­ше  .

До­ка­за­тель­ство:Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

Рис. 6. Чер­теж к при­ме­ру 1

До­ка­жем ме­то­дом «от про­тив­но­го». Пусть ∠А , ∠B , ∠C , тогда ∠А + ∠В + ∠С , это невоз­мож­но, по­сколь­ку ∠А + ∠В + ∠С = .

1. Задание в классе

№ 223, 225, 226, 227.

1. Домашнее задание

Выучить теоремы, знать виды треугольников. № 229,230,231,235.

1. Выводы по уроку

На данном уроке была сформулирована теорема о сумме углов треугольника, теорема о внешнем угле треугольника, были рассмотрены виды треугольников, а также научились решать задачи на применение данных теорем.