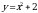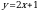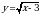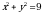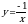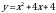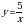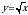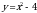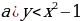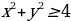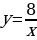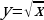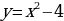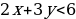Просмотр содержимого документа
«Конспект урока по теме: "Неравенства с двумя переменными"»
Тема урока: Неравенства с двумя переменными.
На уроке применяются элементы следующих современных образовательных технологий:
- Информационно-компьютерные технологии;
- Здоровьесберегающие технологии.
Цели урока:
Образовательные: определение неравенства с двумя переменными; изображение множества решений неравенства с двумя переменными на координатной плоскости.
Развивающие: формирование видов учебно-познавательной деятельности.
Воспитательные: воспитание аккуратности, дисциплины, самостоятельности, трудолюбия, внимания, самоконтроля, интереса к предмету.
Раздаточный материал: Алгоритм нахождения множества решений неравенства.
ТСО: мультимедийное оборудование, презентация.
| Этап урока | Деятельность учителя | Деятельность ученика | Слайд презентации, приложение |
| I Орг. момент | - приветствие; - проверка подготовленности к уроку. |
| 
|
|
II
АОЗ
| По таблице повторить тему «Элементарные функции и их графики». | Формула, задающая функцию | Линия, являющаяся графиком этой функции | | 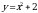
| парабола | | 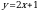
| прямая | | 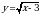
| кривая | | 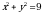
| окружность | | 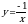
| гипербола | | 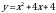
| парабола | Работа по карточкам (3 обучающихся): Карточка 1. Построить график функции: 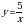 Карточка 2. Построить график функции: 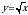 Карточка 3. Построить график функции: 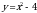
| Самостоятельно выполняют с коллективной проверкой
| слайд 2 |
|
III Проблемное объяснение нового знания | 1) Выполните устно следующее упражнение:
| Учащиеся находят отличия в записанных неравенствах (в 2-х неравенствах - по 1 переменной, в остальных – по две) и записывают тему урока. | 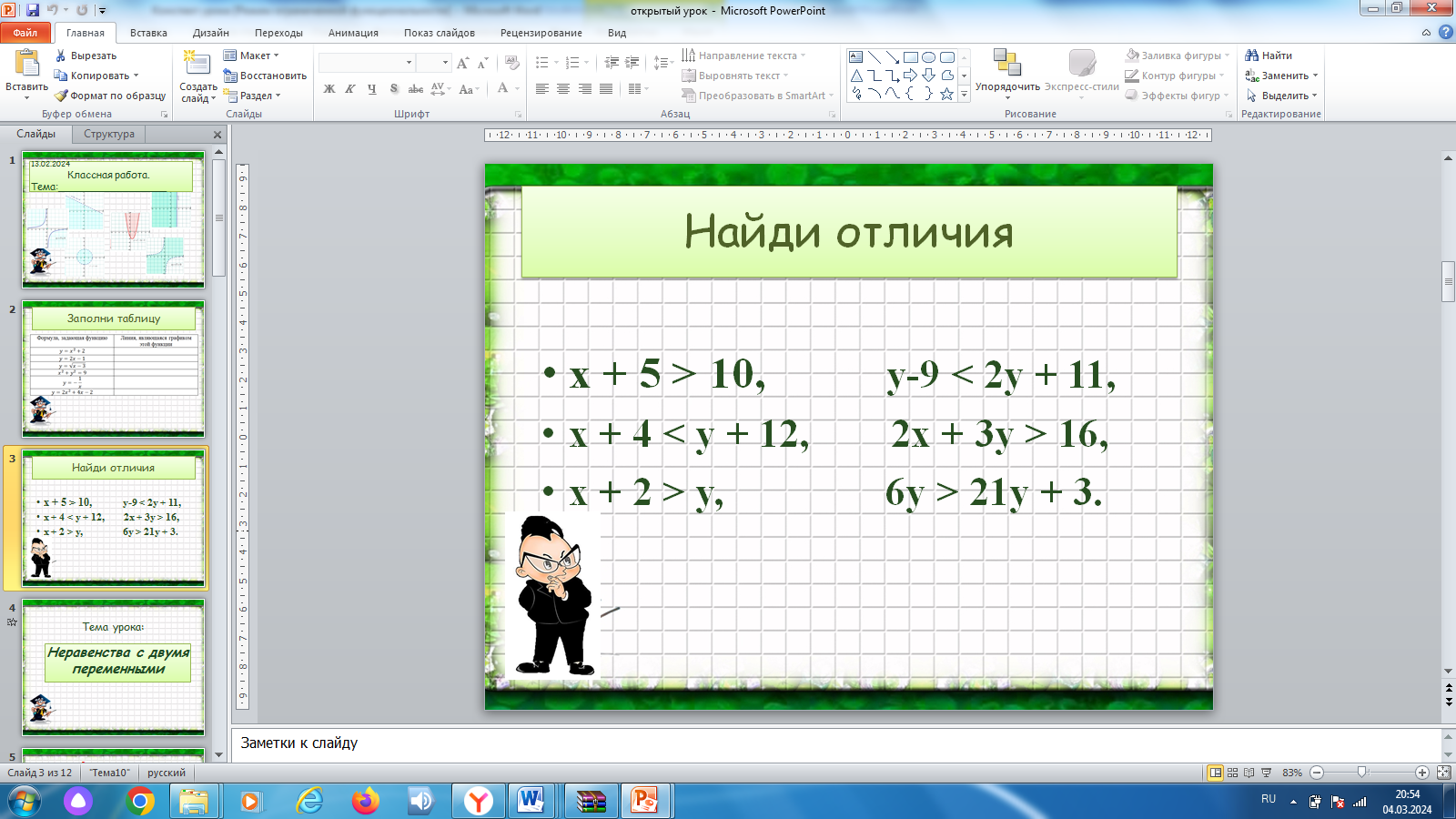
|
| 2) Определение неравенства с двумя переменными.
| Чтение определения по слайду. Запись в тетради. | 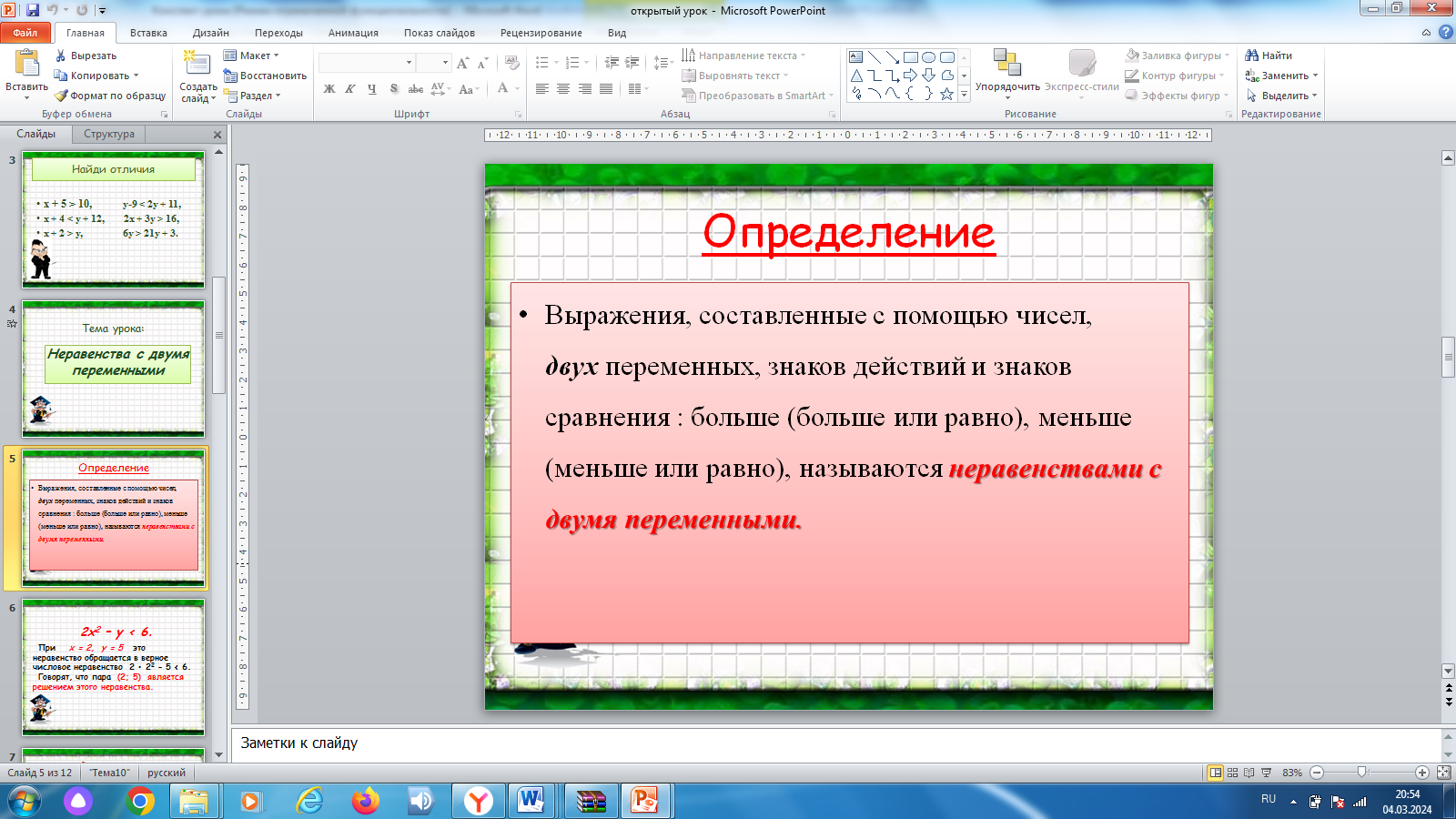 |
|
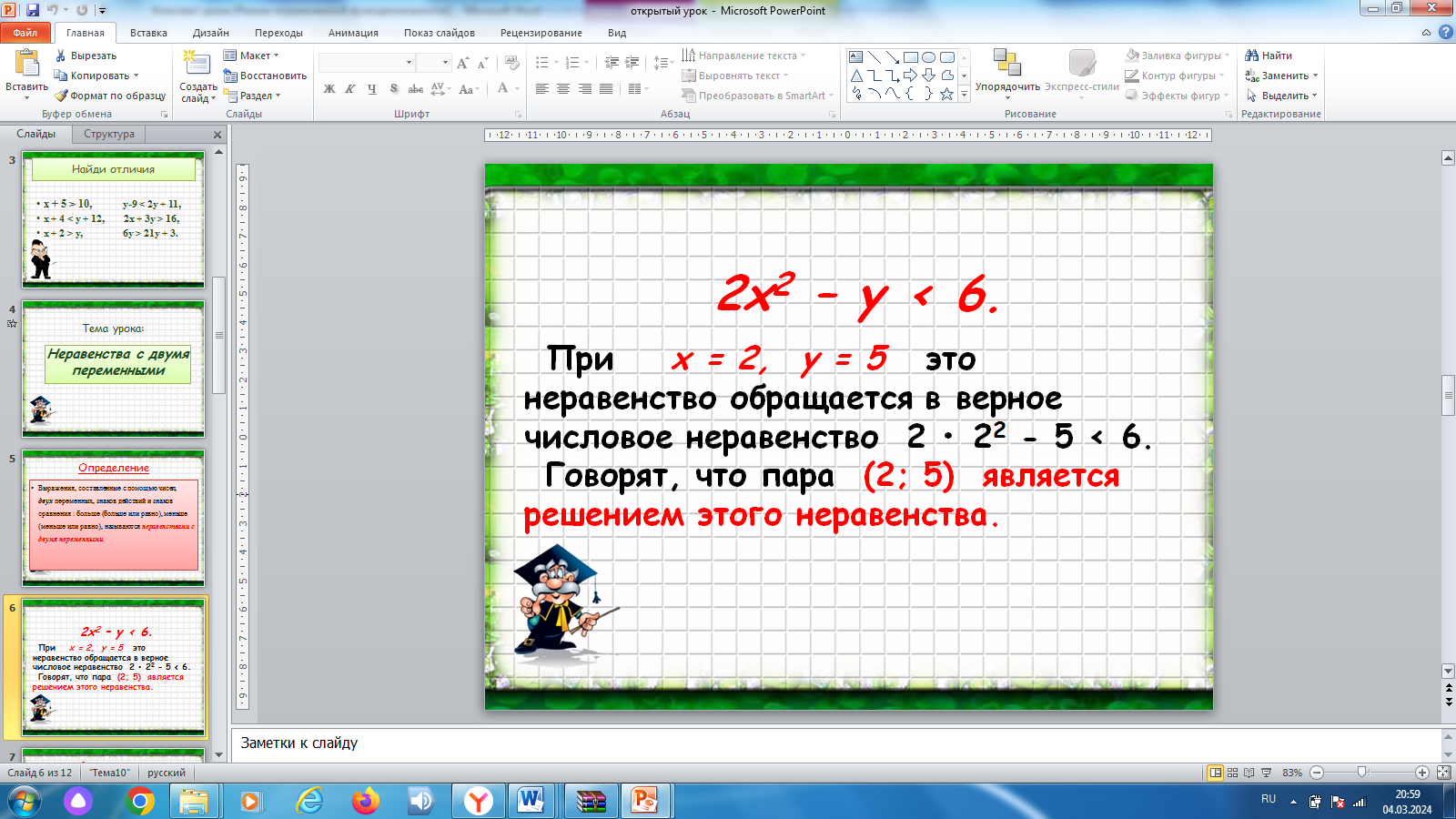
| 3) Рассмотрим неравенство: 2х2 – у 6. При х = 2, у = 5 это неравенство обращается в верное числовое неравенство 2 • 22 - 5 Говорят, что пара (2; 5) является решением этого неравенства.
|
| 
|
| Определение решения неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).
Решаем устно №447 бв, 448 аб. | Чтение определения по слайду. Запись в тетради. №447, б) да в) нет 448 (а,б)
|  |
|
| Чтобы определить множество точек, которые являются решением неравенства с двумя переменными, нужно построить график, преобразовав неравенство в равенство, выразив у через х, построить график, взять контрольную точку, с помощью которой определить решение данного неравенства. Алгоритм, заготовленный заранее учителем, приклеивается в тетрадях учащимися.
| Заполняют пропуски в алгоритмах нахождения множества решений неравенства 2x + 3y . |  |
| IV Физминутка для глаз | Давайте выполним несколько упражнений для снятия напряжения глаз. | Смотрят слайды
|
| V Первичное закрепление во внешней речи
| Закрепим полученные знания.
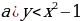
б)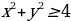
| Решение заданий на интерактивной доске. Построение множества решений неравенства с помощью программы WorkSpace |
|
| VI Самостоятельная работа с самопроверкой |
- решите №446 (б,д), №448(а,б) | Решение номеров самостоятельно. Проверка по слайду |
|
| VII Рефлексия | - С какой темой мы сегодня познакомились на уроке? - Что такое неравенство с двумя переменными? - Что является решением неравенство с двумя переменными? - Как определить на графике множество точек, которые являются решениями неравенства с двумя переменными? |
|
|
| VIII Домашнее задание | № 447, 449
|
Записывают в дневники | 
|
ФАМИЛИЯ ИМЯ кадета____________класс_________
Карточка № 1. Построить график функции 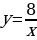
ФАМИЛИЯ ИМЯ кадета____________класс_________
Карточка № 2. Построить график функции 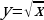
ФАМИЛИЯ ИМЯ кадета____________класс_________
Карточка № 3. Построить график функции 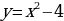
Алгоритм решения
неравенства с двумя переменными
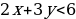
Заменить знак неравенства на равно;
Выразить переменную у через х;
Построить график полученного уравнения
Выделить часть плоскости соответствующую знаку неравенства
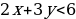
Для этого берем пробную точку из любой части плоскости и подставляем координаты этой точки в неравенство. Если получилось верное числовое неравенство, выделяем часть плоскости, в которой находится пробная точка. Если неверное неравенство – выделяем часть плоскости, которой пробная точка не принадлежит.
14