8 класс АЛГЕБРА Урок № ___
Тема: Определение степени с целым отрицательным показателем.
Тип: урок – изучения нового материала.
Цель: ввести понятие степени с целым отрицательным показателем.
ХОД УРОКА
I. Организационный момент
Учитель и ученики приветствуют друг друга. Выявляются отсутсвующие
II. Cообщение темы и цели урока
III. Изучение нового материала
Окружающий нас мир очень разнообразен и качественно и количественно. Приведём из справочника по физике сведения о массах двух физических тел:
1) масса солнца равна 1,985 ∙ 10-28 г (для простоты ≈ 2 ∙ 1033 г);
2) масса электрона равна 9,108 ∙ 10-28 г (для простоты ≈ 10-27 г).
Обозначение 1033 соответствует произведению тридцати трёх множителей, каждый из которых равен 10. Давайте поймём смысл записи 10-27.
Последовательно запишем степени числа 10 с показателями 0, 1, 2,3, … . Получаем последовательность (ряд) чисел: 100, 101, 102, 103, … В этой записи каждое предыдущее число меньше последующего в 10 раз. Учитывая такую закономерность, распространим нашу запись влево. Перед числом 100 надо написать  , перед числом
, перед числом  запишем число
запишем число  и т.д. Тогда получим последовательность (ряд) чисел: …,
и т.д. Тогда получим последовательность (ряд) чисел: …,  ,
,  ,
,  , 100, 101, 102, 103, ….
, 100, 101, 102, 103, ….
Как было отмечено раннее , закономерность такой последовательности чисел: показатель степени каждого предыдущего числа на 1 меньше показатели степени последующего числа. Поэтому по аналогии с числами, стоящими справа от числа 100, числа, стоящие слева от числа 100, записывают в виде степени числа 10 с отрицательным показателем. Тогда вместо  пишут 10-1, вместо
пишут 10-1, вместо  пишут 10-2 и т.д.
пишут 10-2 и т.д.
Поэтому рассмотренную последовательность чисел:  ,
,  ,
,  , 100, 101, 102, 103, … можно записать в виде: …, 10-3, 10-2, 10-1, 100, 101, 102, 103, … Итак 10-1 означает
, 100, 101, 102, 103, … можно записать в виде: …, 10-3, 10-2, 10-1, 100, 101, 102, 103, … Итак 10-1 означает  , 10-2 означает
, 10-2 означает  и т.д. Такая договорённость принята для степеней с любыми основаниями (кроме нуля). Поэтому получаем следующее определение.
и т.д. Такая договорённость принята для степеней с любыми основаниями (кроме нуля). Поэтому получаем следующее определение.
Если а ≠ 0 и п – целое отрицательное число, то ап =  .
.
Пример 1
По определению степени с целым отрицательным показателем найдём:
а) 2-4 =  =
= 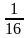 ;
;
б) 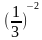 =
= 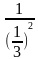 =
= 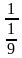 = 9;
= 9;
в) а-3 = 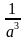 ;
;
г) а-2 b-3 =  ∙
∙  =
= 
Отметим, что выражение 0n при целом отрицательном n и при n = 0 не имеет смысла. При натуральном n выражение 0n имеет смысл, и его значение равно нулю.
Вернёмся к началу нашего урока. Масса электрона составляет примерно 10-27 г =  г = 0,000…01 г. Попутно подчеркнём разнообразие нашего мира: масса Солнца отличается
г = 0,000…01 г. Попутно подчеркнём разнообразие нашего мира: масса Солнца отличается
(26 нулей)
от массы электрона в  =
= =
=  ∙
∙  =
=  = 100 …60 нулей ...0 раз (представить такое различие невозможно).
= 100 …60 нулей ...0 раз (представить такое различие невозможно).
Приведённое определение позволяет решать более сложные задачи.
Пример 2
Вычислим значение выражения 2 ∙ 3-3 + 5 ∙ 9-1 – 4 ∙ 3-2.
Используем определение степени с целым отрицательным показателем и получим:
2 ∙ 3-3 + 5 ∙ 9-1 – 4 ∙ 3-2 = 2 ∙ + 5 ∙
+ 5 ∙  - 4 ∙
- 4 ∙  =
=  +
+  -
-  =
=  .
.
Пример 3
Упростим выражение (у-1 + х-1) ∙  +
+  -1 .
-1 .
Используя определение, получим: (у-1 + х-1) ∙  +
+  -1 = (
-1 = ( +
+  (
( +
+  )-1 =
)-1 =
 ∙ (х + у)-1 =
∙ (х + у)-1 =  ∙
∙ =
=  .
.
Пример 4
С учётом определения имеем:
IV. Решение упражнений
№ 964 – 969; 974; 976; 980.
V. Домашнее задание
Прочитайте 37 пункт
Решить № 970; 973; 977.
VI. Оценивание







 , перед числом
, перед числом  запишем число
запишем число  и т.д. Тогда получим последовательность (ряд) чисел: …,
и т.д. Тогда получим последовательность (ряд) чисел: …,  ,
,  ,
,  .
. =
= 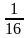 ;
;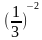 =
= 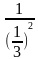 =
= 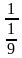 = 9;
= 9;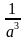 ;
; ∙
∙  =
= 
 г = 0,000…01 г. Попутно подчеркнём разнообразие нашего мира: масса Солнца отличается
г = 0,000…01 г. Попутно подчеркнём разнообразие нашего мира: масса Солнца отличается  =
=









