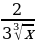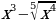Тема урока: Производная.
Цель:
- образовательная: отрабатывать практические навыки в нахождении производных элементарных функций: по определению, по формулам
-воспитательная: формирование навыков контроля и взаимоконтроля, воспитание кругозора, интереса к восприятию нового материала.
-развивающая: развитие внимания, логики, умения сопоставлять факты и делать соответствующие выводы, умения рассуждать и аргументировать свои действия.
Тип урока: комбинированный.
Формы работы: фронтальная, индивидуальная.
Методы: беседа.
Оборудование и дидактический материал: плакаты, карточки для самостоятельной работы.
ХОД УРОКА
1.Организационный момент(1мин).
Учитель: Здравствуйте ребята! По приветствуйте гостей нашего урока.
Открыли тетради и записали число. Мы работаем второй урок по теме «Производная»
Вспомним, о чем мы говорили на прошлом уроке?
Давайте подумаем, чем мы будем заниматься на уроке?
Какие цели и задачи мы поставим перед собой на этот урок?
2. Актуализация знаний(6мин).
1. На прошлом уроке мы ввели понятие предела функции. Вы выучили определение? Кто может ответить на этот вопрос?
Что такое предел функции?

На прошлом уроке мы учились находить пределы функций
Выучили 4 теоремы о пределах (повторим)
| 
| Предел константы, равен константы |
| Постоянный множитель выносится за знак предела |
| Предел суммы, равен сумме пределов |
| Предел произведения, равен произведению пределов |
| Предел частного, равен частному пределу |
Попробуем посчитать пределы
Решение пределов у доски
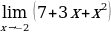
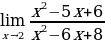
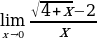
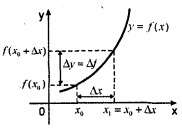
Что такое приращение аргумента, приращение функции?

Давайте вспомним определение производной.

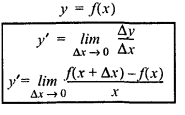
А теперь давайте проверим, как вы на сегодня хорошо выучили формулы дифференцирования, которые мы с вами записали в тетрадь
Проведем маленькую разминку. Я готовилась к уроку и написала формулы, проверьте правильно ли я их записала?
Поиграем. Найди ошибку!
3. Отработка практических навыков
Сейчас каждый ученик получит индивидуальную карточку и будет работать самостоятельно
Работа по карточкам-инструкциям 1 группа
| Инструкция (пример) | Вычислить |
| 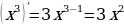
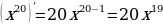
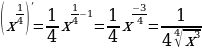 | 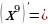 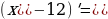 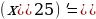 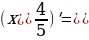
|
| (5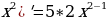 =10x =10x 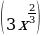 ’ = 3* ’ = 3* 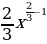 =2 =2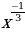
| (6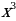 )’ = )’ = (4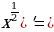 |
| Найти производную функции у = x3−2x2+7x−1 Решение y′=(x3−2x2+7x−1)′=(x3)′−(2x2)′+(7x)′−(1)′= Используя правило производной степенной функции (xp)′=px p−1 имеем: y′=3x3−1−2⋅2x2−1+7−0=3x2−4x+7 Ответ: y′=3x2−4x+7 | у =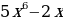
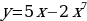
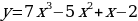
|
2 группа работает у доски и в тетрадях
Используя определение производной, найти f’(x)
f’(x) = 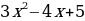
y = 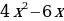 в точке х0 = 2
в точке х0 = 2
После того, как 1 группа выполнила задания на карточках, приступает к решению заданий 2 группы
Карточки – инструкции сдали
Учитель. Хочу обратить ваше внимание, как найти значение степенной функции под знаком радикала. Необходимо вспомнить формулу,
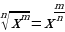
Пример: y = 
Решение
y = 7x4 - 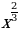
y’ = 7*4x4-1 - 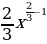 = 28x3 -
= 28x3 - 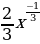 =28x3 -
=28x3 - 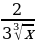
Решить самостоятельно y = 6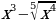
Мы готовимся при изучении этой темы к экзамену ГИА и давайте рассмотрим
задания 1 части некоторых билетов
Билет 5
| Найдите производную функции f x x3 3x 2
|
Билет 6
| Найдите производную функции f x x ex
|
Билет 7
| Найдите производную функции 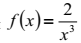 |
Билет 9
| Найдите производную функции 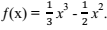 |
Билет 15
| Найти производную функции 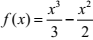
|
Итог урока:
Заслушиваются оценки учеников.
Рефлексия.
Как вы считаете, кто из вас работал в полную силу своих возможностей, чувствовал себя уверенно?
А кто из вас работал хорошо, но не полную силу, испытывал чувство неуверенности, боязни, что отвечу неправильно?
На следующем уроке мы будем изучать правила дифференцирования. По желанию выучить материал наперед
Подготовить сообщение на тему : Геометрический и физический смысл производной. Почему возник такой вопрос?
Изучить п. 45.Решить упражнение 780,791








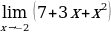
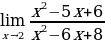
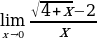



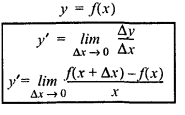
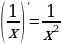

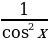
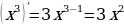
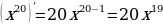
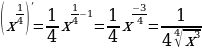
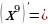
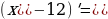
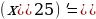
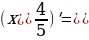
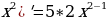 =10x
=10x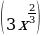 ’ = 3*
’ = 3* 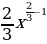 =2
=2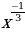
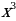 )’ =
)’ = 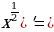
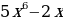
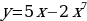
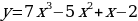
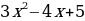
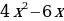 в точке х0 = 2
в точке х0 = 2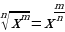
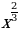
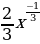 =28x3 -
=28x3 -