Конспект урока геометрии в 10 классе "Признак перпендикулярности двух плоскостей"

Урок геометрии в 10 классе.

Автор учебника: Л.С. Атанасян.

Тема урока: «Признак перпендикулярности двух плоскостей»

Тип урока: Урок изучения нового материала

Цели урока:

Предметные: ввести понятие угла между плоскостями, познакомить учащихся с определением перпендикулярных плоскостей, признаком перпендикулярности двух плоскостей, формировать умение применять его при решении задач.

Личностные: развивать познавательный интерес к предмету, формировать умение представлять результат своей деятельности.

Метапредметные: формировать умение ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.

Планируемые результаты: учащийся научится применять новую теорему при решении несложных задач.

Оборудование: доска, проектор.

Cлова И. Ф. Шарыгина: «Высшее проявление духа — это разум. Высшее проявление разума — это геометрия…»

1. Оргмомент.

2. Актуализация знаний.

Задача: Отрезок АО перпендикулярен Плоскости равнобедренного треугольника АВС с основанием ВС. Найти расстояние от точки О до стороны ВС треугольника АВС, если АО=8, АВ=17, ВС=16.

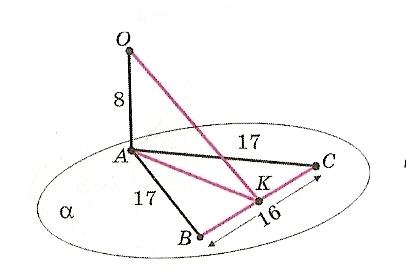
Найти АК, ОК.

Решение: Рассмотрим треугольник АВК – прямоугольный. АК – катет. ВК=16:2=8

ВК=

Рассмотрим треугольник ОАК прямоугольный.

ОК – гипотенуза. ОК=

3. Изучение нового материала.

1) Беседа: Эпиграф. Геометрия и география. Фотопутешествие «Отвесные скалы» - слайды №2-11

2) Целеполагание – слайды №12 - 15

3) Определение - слайд №16

4) Примеры соблюдения перпендикулярности плоскостей в практической деятельности – слайды №17 – 21

5) Формулировка теоремы: «Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны»;

Доказательство проводится по заранее заготовленному чертежу.

Дано:

α, β, AM ⊂ α, AM⏊ β, AM ∩ β = A

Доказать: α ⏊ β

Доказательство:

1) α ∩ β = АР, при этом АМ ⏊ АР, т. к. АМ ⏊ β

по условию, то есть АМ перпендикулярна к

любой прямой, лежащей в плоскости β

2) АТ ⊂ β, AТ ⏊ AР,

∠ТАМ — линейный угол двугранного угла ⇒

∠ТАМ = 90°, т.к. МА ⏊ β ⇒ α ⏊ β

Что и требовалось доказать - слайд №22

6) Следствие: Плоскость, перпендикулярная к прямой,
по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей - слайд №23

4. Первичное закрепление (Устные задачи) - слайд №24

• 1. Верно ли, что две плоскости, перпендикулярные третьей, параллельны?

• 2. Сколько плоскостей, перпендикулярных данной плоскости, можно провести через данную прямую?

• 3. Плоскость α перпендикулярна плоскости β. Будет ли всякая прямая плоскости α перпендикулярна плоскости β?

• 4. Плоскость и прямая параллельны. Верно ли утверждение о том, что плоскость, перпендикулярная данной плоскости, перпендикулярна и данной прямой?

• 5. Плоскость и прямая параллельны. Будет ли верно утверждение о том, что плоскость, перпендикулярная прямой, перпендикулярна и данной плоскости?

5. Решение задач № 178, 180, 181, 182, 183 – слайды №25 – 29

6. Итоги урока. Информация о домашнем задании.

F