КОНСПЕКТ УРОКА ГЕОМЕТРИИ В 9 КЛАССЕ ПО ТЕМЕ "ТЕОРЕМА СИНУСОВ"

Конспект урока геометрии в 9-м классе "Теорема синусов"

Бигманова Рузалия Шамиловна,

 учитель математики МБОУ «Каркалинская ООШ» Лениногорского района РТ

Цель урока:

1. Доказать теорему синусов и показать ее применение при решении задач.

2. Повторить и закрепить: вычисление площади треугольника по двум сторонам и углу между ними, вычисление площади параллелограмма, пропорция, основное свойство пропорции, умение составлять новые пропорции, умение выразить один из членов пропорции через остальные три.

Ход урока

I. Организационный момент. Постановка цели и задач урока.

II. Актуализация опорных знаний.

1. Что значит решить прямоугольный треугольник.

2. Рассказать о ходе решения прямоугольных треугольников:

– по катетам;
– по катету и гипотенузе;
– по катету и острому углу;
– по гипотенузе и острому углу;

III. Мотивация практической необходимости теоремы синусов.

Проверка задач №2 и №3 из домашнего задания.

№1. Дано:

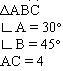
Найти BC – ?

Рис. 1

Решение

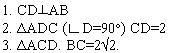
№2. Дано:

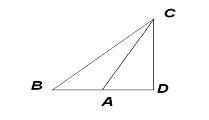
Рис. 2

Решение.

На доске и в тетрадях записывается тема урока, условие теоремы.

IV. Объяснение нового материала.

Теорема синусов: 

Задача.

Дано:

ABC

Доказать:

План доказательства.

1. Провести высоту СD

2. Выразить СD через b и  A.

3. Выразить СD через a и  B.

4. Приравнять полученные для CD выражения.

Рассмотреть доказательства теорем:

1 случай.  A – острый.

Рис. 3

2 случай.  A – тупой.

Рис. 4

Учащиеся выполняют эту работу на местах самостоятельно, а двое из учеников на откидных досках с невидимой для класса стороны.

Затем доказательство разбирается, работа отдельных учащихся оценивается.

V. Формирование умений и навыков. Применение теоремы синусов для решения задач.

1. Двое у доски показывают решение задач №1 и №2 из домашнего задания с помощью теоремы синусов.

2. Решить самостоятельно:

а) а = 20,  A = 75⁰,  В = 60⁰. Найти b.

б) a = 8,7, b = 6,5,  A =45⁰. Найти LB.

в) c = 14,  A = 60⁰,  C = 40⁰. Найти a.

г) LA = 80⁰, a = 16, b = 10. Найти LB.

Ответы изображаются на экране с помощью мультимедийного проектора.

VI. Итоги урока.

1. Ставится вопрос.

Будет ли теорема синусов справедлива для прямоугольного треугольника.

2. Вывод, что теорема синусов справедлива для любого треугольника.

VII. Домашнее задание. №1026(б, г), №1027, № 1029 (учебник геометрии Л.С. Атанасян)

VIII. Рефлексия (Что знал? Что узнал? Что интересного?).