Алгебра 11 класс
Дата: (2 урока)
Тема: Определённый интеграл. Задачи, приводящие к понятию определённого интеграла.
Тип урока: изучение нового материала.
Цель урока:
Образовательные: формирование понятия интеграла; формирование навыков вычисления определенного интеграла; формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.
Развивающие: способствовать развитию познавательных интересов учащихся; содействовать развитию мышления, самостоятельности, наблюдательности;
Воспитательные: прививание интереса к получению знаний; способствовать воспитанию творческой активности учащихся; формирование аккуратности при вычислении интегралов и построения чертежей.
Ученик должен знать: понятие первообразной, таблицу первообразных функций, формулу Ньютона –Лейбница, геометрический смысл определенного интеграла
Ученик должен уметь: вычислять определенный интеграл
Оборудование: Карточки (ДО и после), интерактивная доска
Ход урока:
Актуализация знаний 5мин
| до | понятия | после |
|
| Первообразная, обозначение
|
|
|
| Неопределенный интеграл, запись
|
|
|
| Чему равна первообразная функции у=f(kx+m)?
|
|
|
| Что является первообразной для скорости движения тела?
|
|
|
| Что такое определенный интеграл для данной функции?
|
|
Свяжите все эти понятия и определите тему урока, сформулируйте цели и задачи 3мин
Ответы на обороте доски: 5x; x2; x3; sinx; ln│x│.
Оцените себя на листе опроса.
Ответы пишите во второй столбец.
�а) �; �б)
�; �б) �; �в)
�; �в) �; �г)
�; �г) �; �д)
�; �д) �.
�.
Ответы на обороте доски: �1 � +c; �1
� +c; �1 �+c; �1
�+c; �1 �+c; �
�+c; � �+c; �1
�+c; �1 �+c.
�+c.
ВЫВОД: неопределенный интеграл- это множество первообразных, отличающихся только числом.
Формирование новых знаний
Выявите связь между понятиями, которые я назову, и продолжите этот ряд: 5 и 1/5, умножение и деление, возведение в квадрат и извлечение из-под корня, дифференцирование и… Какой термин будет в паре? Почему? Какие это действия?
Неопределенный интеграл -….
Интеграл, интегрирование, интеграция… Однокоренные слова, к тому же вышедшие за пределы математики и ставшие обиходными. В газетах читаем об интеграции наук, культур, в политике и экономике ведут речь об интегральных процессах.
Любопытно, что идеи интегрального исчисления возникли задолго до появления идей дифференциального исчисления. Греческие математики Эвдокс и Архимед (4; 3 века до н.э.) для решения задач вычисления площадей и объемов придумали разбивать фигуру на бесконечно большое число бесконечно малых частей и искомую площадь (объем) вычисляли как сумму площадей (объемов) полученных элементарных кусочков
Во второй половине 17 века идеи, подготовленные всем предшествующим развитием математики, были гениально осознаны, обобщены и приведены в систему английским физиком и математиком И. Ньютоном и немецким математиком В.Г. Лейбницем. Они создали стройную систему понятий и выработали правила, по которым можно вычислять интегралы.
Сегодня мы будем следовать естественноисторическому развитию математики и искать тот самый скрытый порядок в хаосе…
Геометрический смысл задачи интегрирования.
Какая связь между величинами пути s(t) и v(t) - скорости? -физика
Т.е, s’(t)=v(t) и обратное действие интегрирования дает � �=s(t).
�=s(t).
Таким образом, интеграл скорости равен пути.
 , где S-перемещение,V-скорость, t –время
, где S-перемещение,V-скорость, t –время
 , где m-масса тонкого стержня, ρ- линейная плотность
, где m-масса тонкого стержня, ρ- линейная плотность

 , где A-работа, F-сила, N–мощность
, где A-работа, F-сила, N–мощность
 , гдеq-заряд, I-сила тока.
, гдеq-заряд, I-сила тока.
Рассмотрим, в чем заключается геометрический смысл этого интеграла.

Причем, чем больше будет n, тем точнее будет площадь трапеции. Сумму площадей прямоугольников принято искать в виде предела последовательности (Sn): S=limSn. Итак, мы проделали два шага: разбили отрезок [a,b] на n равных частей и составили сумму Sn прямоугольников. Далее мы можем его вычислить. В курсе мат. анализа доказано, что этот предел в случае непрерывной функции существует. Его называют определенным интегралом от функции y=f(x) по отрезку [a,b] и обозначают так � �. Числа a и b называют пределами интегрирования.
�. Числа a и b называют пределами интегрирования.
Тогда, определение площади из задачи теперь можно записать следующим образом: � �. S –площадь криволинейной трапеции, изображенной на рисунке. В этом состоит геометрический смысл определенного интеграла.
�. S –площадь криволинейной трапеции, изображенной на рисунке. В этом состоит геометрический смысл определенного интеграла.
Если функция y=f(x) непрерывна на отрезке [a,b], то справедлива формула � �, где F(x) – первообразная для f(x). Приведенную формулу называют формулой Ньютона-Лейбница�
�, где F(x) – первообразная для f(x). Приведенную формулу называют формулой Ньютона-Лейбница� �.
�.
| 1 смысл | 2 смысл |
| Это приращение первообразных в концах интервала | Площадь криволинейной трапеции под графиком функции |
Первичная отработка навыков применения новых знаний - взаимопроверка
№49.5-49.7(б) №49.8-49.10(б)
 через понижение степени
через понижение степени
Переходим к карточке и заполняем 2 часть (после)
Самостоятельная работа
Самостоятельная работа Самостоятельная работа
| 1 вариант | 2 вариант |
| 1. 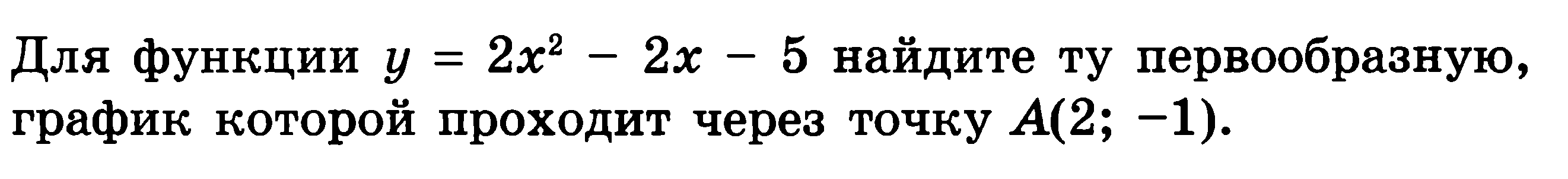
2. 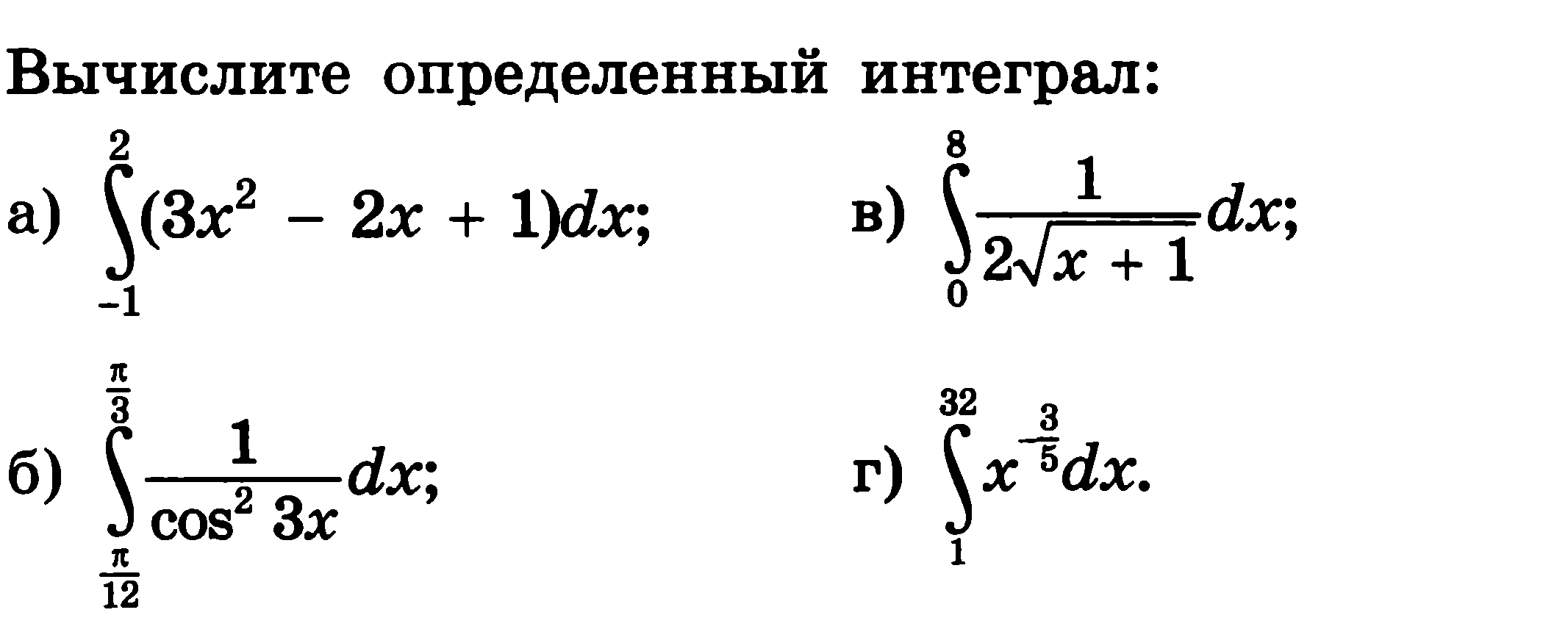
3. На рисунке изображён график некоторой функции  (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x). (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) − F(2), где F(x) — одна из первообразных функции f(x). | 1 2.
3. На рисунке изображён график некоторой функции  (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где (два луча с общей начальной точкой). Пользуясь рисунком, вычислите , где  — одна из первообразных функции — одна из первообразных функции  . . |
Итог урока. Что трудного для вас оказалась? Что было понятным, что не понятным 49.7-49.9(в) формулу знать и знать геометрический смысл







 , где S-перемещение,V-скорость, t –время
, где S-перемещение,V-скорость, t –время , где A-работа, F-сила, N–мощность
, где A-работа, F-сила, N–мощность , гдеq-заряд, I-сила тока.
, гдеq-заряд, I-сила тока.
 через понижение степени
через понижение степени