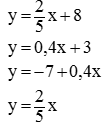Тема урока: Линейная функция. (Слайд 1)
Цель урока.
Обобщить и систематизировать знания учащихся по теме «Линейная функция у = kx + b».
Выработать способности учащихся обобщать частные случаи.
Формировать графическую культуру учащихся и навыки их самостоятельной работы.
Тип урока: урок обобщения
План урока: I. Организационный момент. (блок 1)
II. Проверка знаний учащихся.(блок 2)
III. Лабораторная работа (блок 3)
IV. Физминутка. (блок 4)
V. Интеллектуальная разминка (блок 5)
VI. Самостоятельная работа. (блок 6)
VII. Подведение итогов урока.
VIII. Домашнее задание.
Блок 1 (мотивация) представляет собой специально отобранную систему оригинальных объектов-сюрпризов, способных вызвать удивление учащегося. Этот блок обеспечивает мотивацию учащегося к занятиям и развивает его любознательность.
Сегодняшний урок мы проводим в честь линейной функции. А если какое-то мероприятие проводится в честь кого-то, а в нашем случае в честь чего-то, то это уже (учащиеся могут подсказать) … бенефис. Итак, сегодня урок-бенефис линейной функции.
Мы завершаем тему «Линейная функция», поэтому на уроке вы должны будете продемонстрировать свои знания в честь «Линейной функции». Для начала я приглашаю вас вспомнить некоторые факты. Проводится фронтальный опрос:
– Что такое функция?
– На каком рисунке изображен график функции?
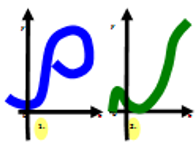 Рис. 1.
Рис. 1.
– Что такое область определения функции?
– Найдите область определения функции
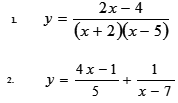
– По графику функции найдите:
1) её область определения;
2) область значений функции.
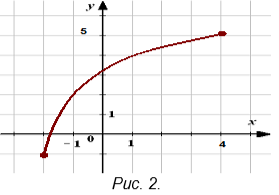
Рис. 2.
На каком рисунке изображён график прямой пропорциональности? Ответ объяснить.
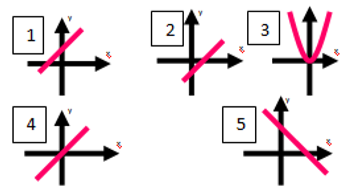 Рис. 3.
Рис. 3.
- Выберите формулы, которые задают линейную функцию:
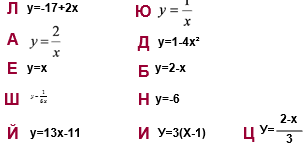 Рис. 4.
Рис. 4.
– Итак, правильный ответ – Лейбниц. Кто это? Тогда давайте посмотрим по слайду, какое отношение к функции имеет Лейбниц (краткая биографическая справка о Лейбнице, о его вкладе в развитие понятия «Функция»).
Блок 2 (содержательная часть) содержит программный материал учебного курса и обеспечивают формирование системного мышления и развитие творческих способностей.
– Молодцы! В честь Линейной функции были показаны неплохие знания!
– Ну, а теперь вперёд, за новыми знаниями!
– Напомните, что является графиком линейной функции? Правильно – прямая.
– А теперь мысленно перенесёмся в геометрию. Вспомним, как на плоскости могут располагаться две прямые? (заслушиваются ответы учащихся)
– Итак, две прямые могут пересекаться, быть параллельны и совпадать.
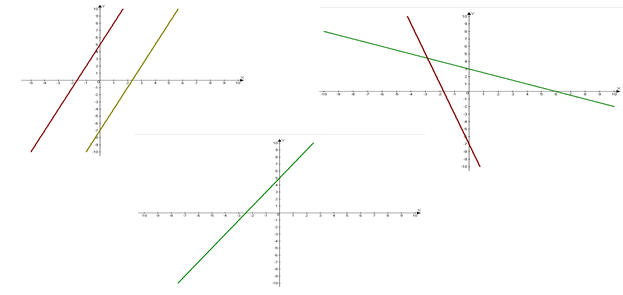 Рис. 5.
Рис. 5.
– Как вы думаете, что же может влиять на расположение прямых на плоскости?
(заслушиваются гипотезы ребят)
– Итак, вернёмся обратно в алгебру и проверим ваши предположения, изучив тему взаимное расположение прямых.
– Для этого проведём лабораторную работу, цель которой выяснить, как влияют коэффициенты k и b линейной функции на их взаимное расположение.
– Повернёмся к мониторам. На всех компьютерах загружена, уже знакомая нам, вспомогательная программа AGrapher, в которой мы и будем рисовать прямые. У каждой группы на столе лежит листок с заданиями и указаниями.
– Вам придется выполнить 3 задания на построение разных прямых, по 2 эксперимента в каждом, и записать выводы в конце каждого задания. Сначала выполните первое задание, покажите готовность к заслушиванию выводов.
Блок 3 .(Лабораторная работа)
Задание № 1
В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 1
| Функция | Коэффициент k |
| У=-2х+3 | k1= |
| У=4х-7 | k2= |
Вывод: Графики двух линейных функций, заданных формулами вида y=kx+b______________________, если коэффициенты k __________________________
Учащиеся делают эксперименты, записывают выводы, некоторые выводы заслушиваются.
– Итак, обобщите (учащиеся должны прийти к выводу: если коэффициенты k1 и k2 в двух линейных функциях различны, то прямые у=k1x+b1 и y=k2+b2 пересекаются).
– Приступаем ко второму заданию.
Задание № 2
В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 3
| Функция | Коэффициент k |
| у=4x-5 | k1= |
| у=4x+1 | k2= |
Вывод: Графики двух линейных функций, заданных формулами вида у=kx+b, ______________________ если коэффициенты k__________________.
– Итак, если все группы справились со вторым заданием, то проверим ваши выводы.
(Заслушивается несколько выводов)
– Итак, если коэффициенты k1 и k2 в двух линейных функциях одинаковы, то прямые у=k1x+b1 и y=k2+b2 параллельны.
– Ну, и приступаем к последнему 3 заданию.
Задание № 3
В одной системе координат постройте графики функций, определите закономерность расположения графиков и сходство в записи формул:
Таблица 6
| Функция | Коэффициент k | Коэффициент b |
| у=-4х-5 | k1= | b1= |
| у=-7х-5 | k2= | b2= |
Запишите вывод:
при одинаковом значении коэффициента ___________ все прямые пересекают ось Оу в точке с координатами ( ; )
Вывод: Если коэффициенты ________ одинаковы, то точка пересечения графиков линейных функций, заданных формулами вида у=kx+b лежит на оси Оу.
– Все группы справились с последним заданием, проверим ваши выводы.
(Заслушивается несколько выводов)
– Итак, если коэффициенты b1 и b2 одинаковы, то прямые у=k1x+b1 и y=k2+b2 пересекаются в точке с координатами (0;b), т.е. лежит на оси Оу.
– Теперь мы знаем условия параллельности и пересечения двух прямых. А в каком случае прямые будут совпадать?
– Правильно, если коэффициенты k1 и k2 двух линейных функциях одинаковы, коэффициенты b1 и b2 одинаковы.
– Отключаем мониторы.
– Давайте упорядочим полученные знания. Я начинаю, а вы продолжаете.
– Прямые параллельны, если…
– Прямые пересекаются, если…
– Прямые совпадают, если…
– Прямые пересекаются в точке, лежащей на оси ординат, если…
Блок 4 (психологическая разгрузка) представляет собой систему психологической разгрузки. Психологическая разгрузка реализуется через упражнения по гармонизации развития полушарий головного мозга, через аутотренинг, через систему спортивно-эмоциональных игр, театрализацию и др.
– Наша помощница мышка предлагает нам, особенно нашим глазам, немного отдохнуть! Встаем!
(Гимнастика для глаз по слайдам презентации в музыкальном сопровождении.)
– Садимся! И снова встаем, пересаживаемся так, чтоб I вариант оставался за монитором, а II вариант – пересаживается за парты.
Блок 5 (интеллектуальная разминка) представляет систему усложняющихся заданий, направленных на развитие мотивации, дивергентного и логического мышления и творческих способностей учащихся.
Отряд французских солдат во время похода в Алжире очутился однажды в местности, совершенно лишенной растительности и притом с почвой настолько болотистой, что, хотя по ней и можно было ступать, сесть на неё было совершенно невозможно. Усталый отряд продвигался вперед в поисках подходящего места для привала, но на десятки вёрст простиралась всё та же болотистая почва. Как отдохнуть, если нет кругом ни единого сухого местечка и ничего такого, что можно было бы подложить или на что можно было бы сесть?
И всё-таки одному солдату пришла в голову счастливая мысль, которая помогла отряду выйти из затруднительного положения. Солдаты уселись и отдохнули.
Как? Отгадайте!
Для решения ребята объединяются в четыре группы по 6 человек, используя приём «мозгового штурма», т. к. его достоинствами являются сравнительная простота и доступность, быстрота генерирования идей, способных стать основой для серьёзного поиска решения.
Блок 6 (самостоятельная работа)
Работаем по слайдам.
Задание № 1
Выясним взаимное расположение прямых:
1) у = - 2х – 1 и у = - 2х + 5;
2) у = - 0,5х и у = 0,5х - 3;
3) у = - х – 4 и у = -х - 4;
Задание № 2
Линейная функция задана формулой
Каким графикам будет параллелен график данной функции?
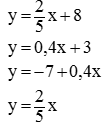
Задание № 3
Задать формулой функцию, график которой параллелен прямой у=-8х+11 и проходит через начало координат
1. у=-8х+1
2. у=-8х
3. у=8х
4. у=11х
Задание № 4
Две прямые пересекаются в точке А (0;4), тогда какое число нужно вставить
у =-11х+4
у = 3х +….
Задание № 5
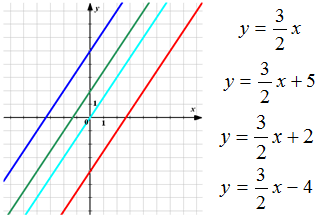
На рисунке изображены графики функций. Укажите, какая формула соответствует каждому из них.
Блок 6 (резюме) обеспечивает обратную связь с учащимися на уроке и предусматривает качественную и эмоциональную оценку учащимся самого урока.
С помощью трёх смайликов (скучно, нейтрально, интересно) учащиеся показывают своё настроение в конце урока и делают самооценку своей работы на уроке.
– Все этапы урока мы сегодня проводили в честь линейной функции. Поработали на славу. Но какой же бенефис без поэтической нотки.
– Поэтому в честь линейной функции мы заслушаем лучшее авторское стихотворение (заранее был объявлен творческий конкурс на лучшее стихотворение, посвященное линейной функции)
Линейной функции посвящается
Не знаю как вам,
А мне всё понятно-
Линейная функция неадекватна.
Она то прямой,
То отрезком бывает,
То ноль, то абсциссу
Одну пресекает.
Или вообще ординате равна-
На оси игрек она залегла.
Но в этом и прелесть,
Изюминка, соль:
Средь функций –
Линейный отрезок-король!
– Думаю, бенефис линейной функции удался.
– Т. к. сегодня вы очень старались и бенефис действительно получился, то домашнего задания не будет.
Муниципальное бюджетное общеобразовательное учреждение
Калининская средняя школа
Урок – бенефис по математике
в 7 классе
«ЛИНЕЙНАЯ ФУНКЦИЯ»
Подготовила и провела
учитель математики
Савина Л.Л.
- 2015 -





 Рис. 1.
Рис. 1.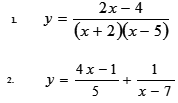

 Рис. 3.
Рис. 3.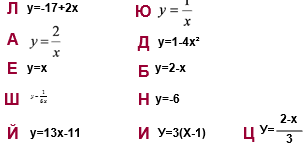 Рис. 4.
Рис. 4. Рис. 5.
Рис. 5.