Конспект урока по математике

Вероятность равновозможных событий.

Цели урока:

Обучающая: познакомить учащихся с понятиями «события достоверные, невозможные, случайные, с классическим определением вероятности, формулой вычисления вероятности событий»

Развивающая: формировать навыки решения задач на характеристику событий и классическое нахождение вероятности события.

Воспитательная: воспитывать умение работать самостоятельно.

Оборудование: раздаточный материал.

План урока:

I. Организационный момент

II. Актуализация знаний учащихся

III. Изучение нового материала

IV. Закрепление изученного материала

V. Подведение итогов урока

VI. Постановка домашнего задания

Ход урока.

1. Организационный момент.

Приветствие учащихся, объявления цели урока

1. Актуализация опорных знаний.

Какой раздел математики мы с вами начали изучать на прошлом уроке? (теорию вероятностей)

Что изучает раздел математики теория вероятностей? (закономерности случайных событий)

Какие события называются случайными? (события которые могут произойти, а могут не произойти)

Какой подход к вычислению вероятностей мы изучали на прошлом уроке? (статистический подход)

В чём заключается статистический подход к вычислению вероятностей? (В результате большого количества испытаний относительная частота появления одного и того же события становится равным определённому числу)

В своём домашнем задании (№ 792) мы тоже присоединились к учёным, которые вычисляли вероятность статистическим способом (послушаем экспертную группу. Французский естествоиспытатель Бюффон (XVIII в.) бросил монету 4040 раз, и при этом герб выпал в 2048 случаях. Следовательно, частота выпадения орла в данной серии испытаний равна: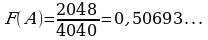

Английский математик Карл Пирсон (1857 – 1936) бросал монету 24000 раз, причем орёл выпал 12012 раз. Следовательно, частота выпадения герба в данной серии испытаний равна:

_{У нашего класса совместными усилиями получились следующие результаты}

Как вы считаете, чем неудобен статистический метод нахождения вероятности? (необходимостью проведения множества испытаний)

1. Изучение нового материала

Сегодня на уроке мы познакомимся с другим подходом к вычислению вероятности, который называется классическим подходом.

Итак, открываем тетради, подписываем число и тему урока «Вероятность равновозможных событий». Как вы считаете с какими понятиями мы должны сегодня познакомиться? ( случайное событие, классический подход к вычислению вероятности)

Встречаясь в жизни с различными событиями, мы часто даем оценку степени их достоверности. При этом произносим. Например, такие слова:

«Это невероятно» - говорим мы о том, что вода в холодильнике закипела

«Маловероятно, что сегодня будет идти дождь» - говорим, глядя на безоблачное небо летним утром

Вопрос о возможности измерения степени достоверности наступления какого-либо события задавали себе многие ученые Основателями теории вероятности были французские математики XVII века Блез Паскаль, Пьер Ферма, и голландский ученый Христиан Гюйгенс

Долю успеха того или иного события математики называют вероятностью этого события (от латинского probabilitas – «вероятность»)

В ряде случаев вероятность события можно оценить непосредственно из условия самого опыта путём рассуждений не прибегая к испытаниям.

Вернёмся к опыту с подбрасыванием кубика. Сколько возможно случаев выпадения очков на игральном кубике при однократном его подбрасывание ? (6 случаев). При этом нет основания считать, что какой – то из исходов более возможен чем другой. Говорят, что существует 6 равновозможных исходов с бросанием кубика.

Исходы в определённом опыте называются равновозможными, если шансы этих исходов одинаковы.

Исходы при котором происходит некоторое событие, называют благоприятными исходами данного события.

Рассмотрим событие В – на кубике выпадает число кратное 2. При каких исходах происходит это событие? (выпадает 2, 4, 6) т.е. Благоприятными являются 3 события.

Отношение благоприятных исходов к общему числу исходов в данном случае равно

Это отношение называется вероятностью события В и записывается

Сформулируйте определение вероятности равновозможных событий:

Вероятностью равновозможного события в некотором испытании равна отношению числа благоприятных для него исходов (n) к числу всех равновозможных событий (m)

Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.

А теперь вернёмся к монетам. Великий французский философ и математик Жан Лерон Даламбер вошел в историю теории вероятностей со своей знаменитой ошибкой, суть которой я предлагаю вам разгадать.

Подбрасываем две одинаковые монеты. Какова вероятность того, что они упадут на одну и ту же сторону?

Опыт имеет три равновозможных исхода:

1. на обе монеты выпадет «орёл»;

2. на обе монеты выпадет «решка»;

3. на одну из монет выпадет «орёл», на другую «решка».

Из них благоприятными будут два исхода:

(он неверно определил равновозможность исходов в опыте всего с двумя монетами)

Правильное решение:

Опыт имеет четыре равновозможных исхода:

1. на обе монеты выпадет «орёл»;

2. на обе монеты выпадет «решка»;

3. на одну из монет выпадет «орёл», на другую «решка»;

4. на одну из монет выпадет «решка», на другую «орёл».

Из них благоприятными будут два исхода.

Даламбер допустил одну из самых распространенных ошибок: он объединил два элементарных исхода в один, тем самым, сделав его не равным по вероятности оставшимся исходам.

Среди всех равновозможных событий выделяются события, которые называются достоверными и невозможными. Попробуйте дать им определение, чему равна их вероятность? (событие которое при проведении данного опыта происходит всегда или никогда, вероятность 1 или 0)

IV. Закрепление изученного материала

1. В ящике находятся 2 белых и 3 черных шара. Наугад вынимается один шар. Какова вероятность того, что вынутый шар

а) белый б) черный

Решение: Существует 5 равновозможных исходов испытания, m = 5

1. число благоприятных исходов n = 2

2. число благоприятных исходов n = 3

Задача №803 ( стр.197)

Самостоятельная работа обучающего характера

Перед вами задания из открытого банка данных ОГЭ, консультируясь в парах решите их.

1. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

2. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

3. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.

4. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.

5. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.

V. Подведение итогов урока

Что нужно знать для нахождения вероятности случайного события?

Для вычисления классической вероятности нужно лишь знать все возможные исходы события и благоприятные исходы. Однако в жизни чаще встречаются события, сравнить и оценить которые, основываясь только интуиции, невозможно и трудно. Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.

- Для чего в школе изучаем теорию вероятности?

Теория вероятностей – один из наиболее важных прикладных разделов математики. Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.

VI. Постановка домашнего задания п. 35; № 736; 864; 807;809

Самостоятельная работа обучающего характера

Перед вами задания из открытого банка данных ОГЭ решите их.

1. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

1. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

2. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.

3. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.

4. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.

________________________________________________________________

Самостоятельная работа обучающего характера

Перед вами задания из открытого банка данных ОГЭ решите их.

1. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками.

1. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер?

2. Игральную кость бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.

3. Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.

4. На экзамене 60 билетов, Олег не выучил 12 из них. Найдите вероятность того, что ему попадется выученный билет.