Тема урока: «Прогрессии».
Тип урока: обобщающий.
Цели:
Образовательная: повторение и обобщение знаний по теме, проверка умения и навыков учащихся, подготовка к ОГЭ.
Развивающая: развитие умения видеть и применять изученные формулы в решении задач; формирование интереса к изучению математики; создавать условия для развития исследовательских и творческих навыков; учить находить главное в потоке информации, анализировать, выдвигать гипотезы и проверяя их, делать выводы.
Воспитательная: создавать условия для повышения интереса к
изучаемому материалу, к активации мыслительной деятельности, развивать
коммуникативные качества учащихся.
развитие умения оценивать свои достижения.
Здоровьесберегающая цель – на протяжении всего урока следить за посадкой учащихся, выстраивать их работу на уроке так, чтобы систематически менялась деятельность учащихся, провести физкультминутку
Планируемые результаты обучения
Личностные: осознание ценностей математического знания, как важнейшего компонента познания реального мира.
Предметные:
Знать определения арифметической и геометрической прогрессий, характеристические свойства арифметической и геометрической прогрессий, формулы п-го члена арифметической и геометрической прогрессий, формулы для нахождения суммы п первых членов арифметической и геометрической прогрессий,
Уметь применять теоретические знания для решения основных типов заданий по теме из открытого банка ОГЭ
Продолжить дальнейшую работу по выработке умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности.
Метапредметные: умение организовать свою деятельность, определять её цели и задачи, умение вести самостоятельный поиск, анализ, отбор информации, умение работать в коллективе; умение учиться в общении со сверстниками; умение высказывать суждения, подтверждая их фактами.
Компетенции, формируемые на уроке
Общекультурные, учебно-познавательные, информационные, коммуникативные.
УУД
Личностные УУД: развитие познавательных интересов, учебных мотивов, осознают необходимость изучения математики, проявляют положительное отношение к урокам математики, интерес к прочному усвоению учебного материала, способам решения учебных задач, доброжелательное отношение к сверстникам; стимулирование стремления к саморазвитию, формирование самооценки.
Регулятивные УУД: целеполагание - как способность соотносить то, что уже известно и усвоено, и то, что еще неизвестно; планирование - как определение последовательности промежуточных целей с учетом конечного результата; оценка - как выделение и осознание того, что уже освоено и что еще подлежит усвоению; осознание качества и уровня усвоения; принимают и формулируют учебную проблему, определяют цель учебной деятельности с помощью учителя и самостоятельно, осуществляют поиск средств её достижения, используют наряду с основными и дополнительные средства получения информации.
Коммуникативные УУД: включаемость в коллективное обсуждение вопросов, постановка вопросов, умение слушать и вступать в диалог, инициативное сотрудничество в поиске и сборе информации, умение аргументировать свою точку зрения.
Познавательные УУД: анализировать, сравнивать, классифицировать и обобщать, самостоятельно предполагают, какая информация нужна для решения предметной учебной задачи, поиск и выделение необходимой информации, выбор способа действия, умение осознанно применять полученные знания на практике, умение осознанно строить речевое высказывание в устной форме.
Необходимое оборудование:
Раздаточный материал;
Мультимедиа - проектор;
Компьютер;
ХОД УРОКА.
 Этап 1. Самоопределение к деятельности:
Этап 1. Самоопределение к деятельности:
Цели этапа:
включить учащихся в учебную деятельность;
определить содержательные рамки урока.
Учитель: Здравствуйте, ребята. Я рада видеть всех вас.
(На доске в столбик записаны слова: хочу, могу, умею, делаю) учитель, показывая на каждое из этих слов, даёт расшифровку.
Сегодня на уроке я:
ХОЧУ: ………… я хочу пожелать вам, ребята, увеличить объём своих знаний; хочу пожелать вам «Ни пуха, ни пера!».
МОГУ: …………
я могу быть вашим консультантом
на уроке можно ошибаться, сомневаться, консультироваться.
УМЕЮ: …………….
прийти на помощь
применять рациональные способы для решения задач.
ДЕЛАЮ: ………….
делаем каждый себе установку «Понять и быть тем первым, который увидит
ход решения».
Вступительное слово учителя:
Эта история произошла давным-давно. В древнем городе жили добрый мудрец и злой человек, который завидовал славе мудреца. И решил он придумать такой вопрос, чтобы мудрец не смог на него ответить. Пошел он на луг, поймал бабочку, сжал ее между сомкнутых ладоней и подумал: "Спрошу-ка я: о, мудрейший, какая у меня бабочка - живая или мертвая? Если он скажет, что мертвая, я раскрою ладони - бабочка улетит, а если скажет - живая, я сомкну ладони, и бабочка умрет". Так завистник и сделал: поймал бабочку, посадил ее между ладоней, отправился к мудрецу и спросил его: "Какая у меня бабочка - живая или мертвая?" Но мудрец ответил: " Все в твоих руках:"
Бывают моменты в жизни, когда руки опускаются и кажется, что ничего не получится. Тогда вспомните слова мудреца "Все в твоих руках" и пусть эти слова будут девизом нашего урока.
Наше познание курса алгебры можно сравнить с походом в горы и сегодня мы с вами преодолеем ещё одну математическую вершину. А теперь давайте проверим, готовы ли вы к восхождению.
Этап 2. Актуализация знаний по теме «Прогрессии»
 Цели этапа:
Цели этапа:
актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала;
актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний.
Учитель: Для того, чтобы вы лучше поняли новый материал и смогли активно включиться в работу на уроке вспомним, что мы уже знаем, отвечая на вопросы. Подобную работу мы уже проделывали, Вы с ней прекрасно справились. Попробуем закрепить наш успех. Для того, чтобы вы могли быстро и активно работать у вас на столах лежит подготовленный заранее раздаточный материал:
Какие прогрессии вы изучили? (арифметическая и геометрическая)
Дадим определение им.
Чем похожи?
Чем отличаются?
даны последовательности чисел. Какие это последовательности?
13; 10; 7; 4;…(арифметическая)
1; 3; 9; 27;…(геометрическая)
1;3;4;5;…(последовательность)
24; 12; 6; 3;…(геометрическая)
5; 10; 25; 100;..(последовательность)
0,5;1;1,5;2;… (арифметическая)
Чему равна разность арифметических прогрессий? (d=-3, d=0,5)
Найдите следующие три члена прогрессий.
(следующие члены : 1) 1, -2, -5;
2) 2,5; 3; 3,5;
8) Чему равен знаменатель геометрических прогрессий? (q = 3, q = 0,5)
9) Найдите следующие три члена прогрессий.
(следующие члены: 1)81; 243; 729.
2) 1,5; 0, 75; 0, 375
- Для решения задач по теме «Прогрессии» что необходимо знать?. (Формулы)
- Чтобы решить ту или иную задачу по этой теме, нужно знать формулы. Проверим знание формул по теме “Арифметическая и геометрическая прогрессии”.
| № | Прогрессии | Арифметическая (an) | Геометрическая ( bn) |
| 1 | Определение | | |
| 2 | Формула для нахождения n-го члена | | |
| 3 | Сумма n-первых членов прогрессии | | |
| 4 | Свойства | | |
3.Этап закрепления знаний и совершенствования способов действий.

Цели этапа:
нового способа действия, устраняющего причину выявленного
затруднения;
содействовать усвоению учащимися изученных знаний, применение их в практических заданиях, установить правильность и осознанность изученного материала; выявить пробелы в знаниях учащихся.
Провести коррекцию выявленных пробелов в знаниях учащихся
Учитель организует учебное взаимодействие в группах. Предлагает работать по алгоритму. Контролирует работу учащихся, оказывает индивидуальную помощь.
- Объединимся в группы для решения задач. (Решение задач в группах с последующей проверкой) Данные задания соответствуют типам заданий ОГЭ (№6)
Выполнение заданий
| Арифметическая (an) | Геометрическая ( bn) |
| 1) Дано: (а n) арифметическая прогрессия а1 = 5,d = 3 . Найти: а6 ; а10. Решение: используя формулу а n = а 1+(n -1) d а6 = а1+5 d = 5+ 3· 5 = 20 а10 = а1+9 d = 5+ 3· 9 = 32 Ответ: 20; 32 | 2) Дано: (bn) геометрическая прогрессия b1= 5 ,q = 3 . Найти: b3 ;b5. Решение: используя формулу bn= b1qn-1 b3 =b1q2 = 5 ·32 =5· 9=45 b5 =b1q4 = 5 ·34 =5 · 81=405 Ответ:45; 405. |
| 3)Дано: (а n) арифметическая прогрессия а4=12,5; а6=17,5. Найти: разность арифметической прогрессии. Решение: используя свойство 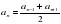 арифметической прогрессии имеем: 
d =15- 12,5= 2,5 Ответ: 2,5 | 4) Дано: (bn) геометрическая прогрессия b4=6; b6=24. Найти: знаменатель геометрической прогрессии, если известно, что он положительный. Решение: используя свойство  геометрической прогрессии имеем:  2) q = 12:6=2. Ответ: 2 |
| 5) Дано: (а n) арифметическая прогрессияа1 = 11,d = 2 . Найти: S10 . Решение: а10 = а1 +9 d =29 используя формулу Sn имеем: 
Ответ: 200. | 6) Дано: (bn) геометрическая прогрессияb1= 40 ,q = 2 . Найти: S5. Решение: используя формулу Sn имеем: 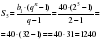 Ответ: 1240. |
Этап психологической разгрузки.
У Вас на столах лежат листы, на которых написаны цифры от 1 до 9. Теперь раскрасьте ряд двумя разными цветами в любом порядке.
А пока Вы раскрашиваете, я расскажу про замечательного математика по фамилии Рамсей. Он жил в начале ХХ века. Им была создана теория, доказывающая, что в мире нет абсолютного хаоса. Что даже, казалось бы, самая неупорядоченная система имеет определенные математические закономерности. Вспомните, когда Вы смотрите на звезды, то может показаться, что расположены они в самом случайном порядке. Но еще в древности люди увидели там созвездия.
И вот на ваших карточках казалось бы цифры раскрашены в случайном порядке. Но Рамсей доказал, что это не так, доказав следующий факт: Обратите внимание, что хотя бы три каких – либо числа одного цвета обязательно составляют арифметическую прогрессию. Как я это сделала, показано на слайде. Какие числа образуют прогрессию? (3, 6, 9)
Найдите такие числа в своих рядах.

Этап закрепления знаний и совершенствования способов действий.
Использование прогрессий при решении практических задач
Математика – наука очень древняя и возникла из практических нужд
человека. Видимо, и прогрессии имеют определенное практическое значение. В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко второму тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий. Вот пример задачи из египетского папируса Ахмеса: «Пусть тебе сказано: раздели 10 мер ячменя между 10 человеками и, разность же между каждым человеком и его соседом равна меры».
Задачи на прогрессии, дошедшие до нас из древности, были связаны с
Запросами хозяйственной жизни: распределение продуктов, деление наследства и другие.
В связи свыше перечисленными фактами были поставлены перед вами
задачи:
- Изучить в каких областях жизни используются прогрессии
Решить задачи из разных областей знаний
О некоторых результатах своей работы вы сейчас нам расскажете.
Учащиеся решают у доски задачи,которые они заранее подготовили
Прогрессии в литературе
вспомним строки из "Евгения Онегина".
...Не мог он ямба от хорея,
Как мы не бились отличить...
Давайте вспомним, что же такое ямб и хорей.
Ямб - это стихотворный размер с ударением на чётных слогах 2; 4; 6; 8... Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и разностью прогрессии 2.
Ямб «Мой дЯдя сАмых чЕстных прАвил...»
Прогрессия: 2; 4; 6; 8...
Хорей - это стихотворный размер с ударением на нечётных слогах стиха. Номера ударных слогов образуют арифметическую прогрессию 1; 3; 5; 7... С первым членом 1 и разностью прогрессии 2.
Хорей «Я пропАл, как звЕрь в загОне» (Пастернак)
Прогрессия: 1; 3 ;5; 7...
Классический хорей:
Листья падают в саду…
В этот старый сад, бывало,
Ранним утром я уйду
И блуждаю, где попало. (И. Бунин)
Вот ещё хорей (тоже из Бунина):
Яблони и сизые дорожки,
Изумрудно-яркая трава
На берёзах — серые серёжки
И ветвей плакучих кружева.
«Буря мглОю нЕбо крОет»
А.С. Пушкин, прогрессия 1; 3; 5;7.
Исторические задачи:
1.Задача -легенда
Индийский царь Шерам позвал к себе изобретателя шахматной игры, своего подданного Сету, чтобы наградить его за остроумную выдумку. Сета, издеваясь над царем, потребовал за первую клетку шахматной доски 1 зерно, за вторую — 2 зерна, за третью — 4 зерна и т. д. Обрадованный царь посмеялся над Сетой и приказал выдать ему такую «скромную» награду. Стоит ли царю смеяться?
Решение:
Дано: ; 1, 2, 4, 8, 16…
q=2, n = 64
Сумма равна 18 446 744 073 709 551 615
2.Идеи Мальтуса
В первоначальной формулировке Мальтуса, численность населения
увеличивается в геометрической прогрессии (1, 2, 4, 8, 16 и т.д.), а производство продуктов питания — в арифметической прогрессии (1, 2, 3, 4, 5 и т.д.). По Мальтусу, именно этот разрыв и является причиной многих общественных бед
— бедности, голода, эпидемий, войн
ФИЗИКА
а) Нейтрон, ударяя по ядру урана, раскалывает его на две части.
Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам,
Раскалывает их еще на 4 части и т.д. – это геометрическая прогрессия.
б) При свободном падении тело прошло в первую секунду 5м, а в каждую
следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с. после начала падения.
в) Улитка ползет по дереву. За первую минуту она проползла 30 см, а за
Каждую следующую минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка вершины дерева длиной 5,25 м, если считать, что движение начато от его основания?
Решение:
a1 =30, d=5, Sn= 525, n0.
Sn= (2a1+ d (n-1))n:2; 525= (2·30+ 5 (n-1))n:2; 1050= (60+ 5 (n-1))n;
1050= 55 n + 5n2;
n2 +11 n -210=0, n1=-21, n2=10 (n0).
Улитка достигнет вершины за 10 дней.
О финансовых пирамидах:
Разберёмся в механизмах этих организаций. Организатор начинает
Вовлекать в свою организацию и говорит, что, если внести указанную плату по указанным адресам по 1 рублю, а затем заплатить ещё по 5 таким же адресам, вычеркнув первый адрес и дописав свой последним, то через некоторое время вы получите уйму денег. Хотя желающих разбогатеть по щучьему веленью немало, но в выигрыше оказываются только учредители такой игры.
Решение:
Дело в том, что число участников увеличивается в 5 раз с каждым кругом.
Если пятёрка устроителей подпишет, допустим, 120 человек со своими
адресами, то в первом круге участвуют 120 человек, во втором – 600, в третьем – 3 000, …, в десятом – 234 375 000 человек; это намного больше населения страны. Так что участник, включившийся в восьмом или девятом круге, уже ничего не получит.
БИОЛОГИЯ
Все организмы обладают интенсивностью размножения в геометрической
прогрессии.
1. Инфузории
Летом инфузории размножаются бесполым способом делением пополам.
Вопрос: сколько будет инфузорий после 15-го размножения?
b15 = 2∙214 = 32 768
2. Известно, что бактерии размножаются делением: одна бактерия делится
на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением.
Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.
3. Бактерия, попав в живой организм, к концу 20-й минуты делится на две
бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу
суток.
Решение:
В сутках 1440 минут, каждые двадцать минут появляется новое поколение -
за сутки 72 поколения. По формуле суммы n первых членов геометрической
прогрессии, у которой b1=1, q=2, n=72, находим, что S72=272-1= 4 722 366 482869 645 213 696 - 1== 4 722 366 482 869 645 213 695.
Учитель
Мы увидели, что прогрессии встречаются при решении задач в медицине, в
строительстве, в банковских расчетах, в живой природе, в спортивных
соревнованиях и в других жизненных ситуациях. Следовательно, многим
необходим навык применения знаний, связанных с прогрессиями.
6. Рефлексия.
 Цели этапа:
Цели этапа:
направления будущей учебной деятельности;
Учитель. Сегодня на уроке вы получили дополнительный жизненный опыт. Возвращаясь к эпиграфу нашего урока, я хочу узнать, действительно ли был прав мудрец "Все в твоих руках" ?
- Что нового узнали на уроке?
Трудным ли для вас было покорение новой математической вершины, я бы хотела узнать где вы находитесь - по-прежнему у подножия горы, на средине пути или на вершине, изобразите себя на заранее приготовленных листах.
Надеюсь, что знания, умения, навыки, полученные на уроке, помогут вам лучше ориентироваться в окружающем мире, а задания на прогрессии станут для вас более понятными и привлекательными.
Учитель: Большое спасибо за урок! Мне очень понравилось с вами работать!
А теперь давайте оценим вашу работу на сегодняшнем уроке. Каждый из вас во время урока выполнял разнообразные задания, и лучше вас никто не знает, какой вклад внес каждый в общее дело. Поэтому, я предлагаю вам оценить свою работу. Для этого воспользуйтесь оценочными бланками, лежащими перед вами.
не забудьте отметить, как вы оцениваете свою деятельность на уроке
P.S. Я оставляю за собой право подкорректировать выставленные оценки, потому что я также следила за работой каждого из вас на уроке.
Домашнее задание:
1. Подготовить выступления о жизнедеятельности К. Гаусса и Л. Ф. Магницкого.
2. Подобрать «исторические» задачи по теме «Прогрессии».





 Этап 1. Самоопределение к деятельности:
Этап 1. Самоопределение к деятельности: Цели этапа:
Цели этапа: 
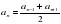




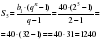

 Цели этапа:
Цели этапа: 









