Конспект урока по теме:"Сфера.Взаимное расположение сферы в плоскости"

Мы продолжаем знакомство со сферой.

На прошлом занятии вы узнали, что в прямоугольной системе координат О_xyz уравнение сферы с центром

С (x₀ ; y₀ ; z₀) и радиусом R имеет вид:

(x-x₀)²+(y-y₀)²+(z-z₀)² = R²

Уравнение сферы с центром

С( x₀ ; y₀ ; z₀) и радиусом R:

(x-x₀)²+(y-y₀)²+(z-z₀)² = R²

Рассмотрим взаимное расположение плоскости и сферы в зависимости от соотношения между расстоянием от её центра до плоскости и радиусом сферы.

1.Выберем прямоугольную систему координат О_xyz так, что центр сферы радиуса R имеет координаты С (0;0;d), где d-расстояние от центра сферы до данной плоскости α, а сама плоскость α совпадает с координатной плоскостью О_xy.

2.Запишем уравнение данной сферы:

x²+y²+(z- d)² = R².

3.Очевидно, что аппликата z любой точки плоскости О_xy равна нулю, то есть координаты любой точки плоскости О_xy удовлетворяют уравнению z=0, а координаты любой точки, не принадлежащей плоскости О_xy, этому уравнению не удовлетворяют, так как аппликаты таких точек не равны нулю.

Тем самым в соответствии с понятием уравнения поверхности, уравнение z=0 является уравнением координатной плоскости О_xy, таким образом, уравнение плоскости α имеет вид:

z=0.

4.Взаимное расположение сферы и плоскости зависит от решения системы уравнений:

z=0

x²+y²+(z- d)² = R².

При z=0 второе уравнение примет вид:

x²+y² = R²- d²

1.Прямоугольная система координат О_xyz .

Центр сферы С(0;0;d),радиус R ,

d-расстояние от центра сферы до плоскости α,

плоскость α совпадает с координатной плоскостью О_xy.

2. Уравнение данной сферы:

x²+y²+(z- d)² = R².

3. Уравнение плоскости α:

z=0

4. z=0

x²+y²+(z- d)² = R².

z=0 ⇒ x²+y² = R²- d²

Рассмотрим возможные три случая:

1) Расстояние от центра сферы до плоскости меньше радиуса сферы

d R. Тогда R²- d²0 и уравнение x²+y² = R²- d² является уравнением окружности радиуса

r=√ R²- d² , все точки этой окружности принадлежат одновременно и сфере и плоскости.

Итак, плоскость и сфера пересекаются по окружности.

Таким образом, если расстояние от центра до плоскости меньше радиуса сферы, то сечение сферы данной плоскостью является окружностью.

1. dR R²- d²0

Уравнение x²+y² = R²- d² является

уравнением окружности радиуса

r=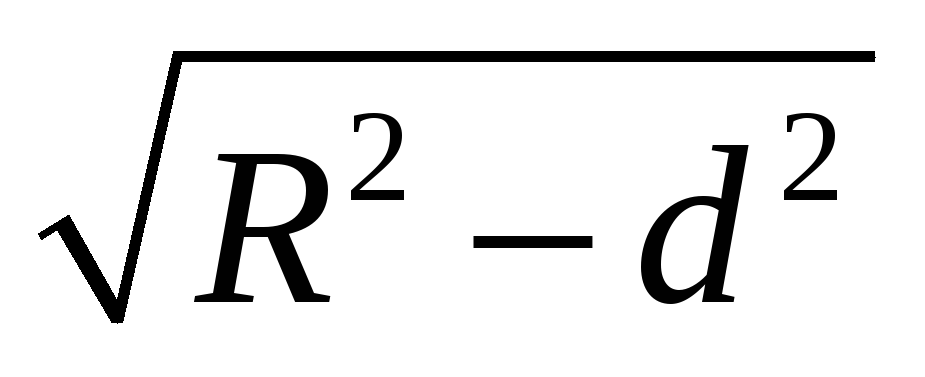, все точки этой окружности принадлежат одновременно и сфере и плоскости.

Если расстояние от центра до плоскости меньше радиуса сферы, то сечение сферы данной плоскостью является окружностью.

Очевидно, что сечение шара плоскостью является кругом, причем:

если секущая плоскость проходит через центр шара, то в сечении получается круг, радиус которого равен радиусу шара;

если секущая плоскость не проходит через центр, то в сечении получается круг, радиус которого меньше радиуса шара.

Сечение шара плоскостью- круг.

1. Секущая плоскость проходит через центр шара- в сечении получается круг, радиус которого равен радиусу шара. Такой круг называется большим кругом шара.

2. Если секущая плоскость не проходит через центр, то в сечении получается круг, радиус которого меньше радиуса шара.

2). Расстояние от центра сферы до плоскости равно радиусу сферы

d=R, тогда R²- d²=0 и уравнению

x²+y² = R²- d² удовлетворяют только значения

x=0, y=0. Поэтому только координаты точки О (0;0;0) удовлетворяют обоим уравнениям, итак точка О — единственная общая точка плоскости и сферы.

Таким образом, если расстояние до плоскости равно радиусу сферы, то плоскость и сфера имеют единственную общую точку.

2) d=R ⇒ R²- d²=0 ⇒ x²+y²=0

Единственное решение: x=0, y=0

О(0;0;0)- единственная общая точка плоскости и сферы.

Если расстояние до плоскости равно радиусу сферы, то плоскость и сфера имеют единственную общую точку.

3) Расстояние от центра сферы до плоскости больше радиуса сферы

d  R, в этом случае R²- d² 0 и уравнение

x²+y² = R²- d² не имеет решения.

Таким образом, если расстояние от центра сферы до плоскости больше радиуса сферы, то плоскость и сфера не имеют общих точек.

3) d  R ⇒ R²- d² 0 ⇒

уравнение x²+y² = R²- d² не имеет решения.

Если расстояние от центра сферы до плоскости больше радиуса сферы, то плоскость и сфера не имеют общих точек.

Применим полученные знания при решении задач.

Задача 1

Шар с радиусом 41 дм пересечён плоскостью, проходящей на расстоянии 9 дм от центра. Найти площадь сечения.

Решение:

1.Расстояние от центра шара до секущей плоскости меньше радиуса, значит сечением шара плоскостью, является круг.

Площадь круга вычислим по формуле:

S=πr², где r = АК — радиус круга.

2.Найдём АК из прямоугольного треугольника

АОК по теореме Пифагора:

А

3. S_сеч=r²=*40²=1600(дм²).

Таким образом, площадь сечения равна 1600 дм².

Дано: шар, R=41 дм, d=9 дм

Найти: S_сеч

Решение:

1. d R ⇒ сечение шара плоскостью- круг.

S=r², r=АК -радиус круга.

2. Δ АОК-прямоугольный.

По теореме Пифагора:

АК= = =

= =40дм

3. S_сеч=πr²=π·40²=1600π (дм²).

Ответ: S_сеч=1600π (дм²).

Сегодня мы рассмотрели возможные случаи взаимного расположения сферы и плоскости, применили свои знания при решении задач.