

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Контрольные задания по ТВ и МС
Категория:
Математика
19.11.2016 18:09




 задан в виде таблицы. Найти: математическое ожидание
задан в виде таблицы. Найти: математическое ожидание  ; дисперсию
; дисперсию  ; среднее квадратическое отклонение
; среднее квадратическое отклонение  ; построить многоугольник распределения.
; построить многоугольник распределения.

 . Построить полигон относительных частот. Найти: несмещенные оценки генеральной средней
. Построить полигон относительных частот. Найти: несмещенные оценки генеральной средней  и генеральной дисперсии
и генеральной дисперсии  ; моду
; моду  , медиану
, медиану 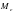 и размах варьирования
и размах варьирования  .
. 










