Контрольная работа № 3 по теме «Интеграл и его применение»
Вариант 1
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой 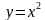 и прямыми y = 0 и x = 3.
и прямыми y = 0 и x = 3.
3. Найдите первообразную функции 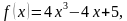 график которой проходит через точку A (1; 6).
график которой проходит через точку A (1; 6).
4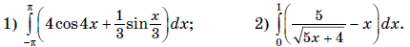 . Вычислите интеграл:
. Вычислите интеграл:
5. Найдите площадь фигуры, ограниченной графиками функций 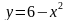 и y = x + 4.
и y = x + 4.
6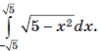 . Используя геометрический смысл интеграла, вычислите
. Используя геометрический смысл интеграла, вычислите
Вариант 2
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой 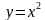 и прямыми y = 0 и x = 2.
и прямыми y = 0 и x = 2.
3. Найдите первообразную функции 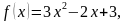 график которой проходит через точку M (1; −3).
график которой проходит через точку M (1; −3).
4. Вычислите интеграл:
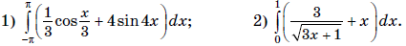
5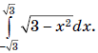 . Найдите площадь фигуры, ограниченной графиками функций
. Найдите площадь фигуры, ограниченной графиками функций 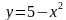 и y = 3 – x .
и y = 3 – x .
6. Используя геометрический смысл интеграла, вычислите
Вариант 3
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой 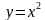 и прямыми y = 0 и x = 1.
и прямыми y = 0 и x = 1.
3. Найдите первообразную функции 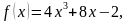 график которой проходит через точку A (1; 3).
график которой проходит через точку A (1; 3).
4. Вычислите интеграл:
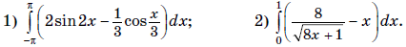
5. Найдите площадь фигуры, ограниченной графиками функций 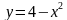 и y = x + 2.
и y = x + 2.
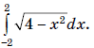
6. Используя геометрический смысл интеграла, вычислите
Вариант 4
1. Вычислите интеграл:

2. Найдите площадь фигуры, ограниченной параболой 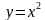 и прямыми y = 0 и x = 4.
и прямыми y = 0 и x = 4.
3. Найдите первообразную функции 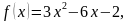 график которой проходит через точку M (1; 4).
график которой проходит через точку M (1; 4).
4. Вычислите интеграл:
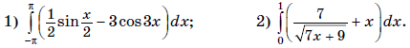
5. Найдите площадь фигуры, ограниченной графиками функций 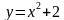 и y = x + 4.
и y = x + 4.
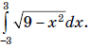
6. Используя геометрический смысл интеграла, вычислите








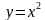 и прямыми y = 0 и x = 3.
и прямыми y = 0 и x = 3. 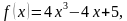 график которой проходит через точку A (1; 6).
график которой проходит через точку A (1; 6). 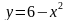 и y = x + 4.
и y = x + 4. 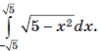 . Используя геометрический смысл интеграла, вычислите
. Используя геометрический смысл интеграла, вычислите 
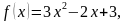 график которой проходит через точку M (1; −3).
график которой проходит через точку M (1; −3). 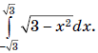 . Найдите площадь фигуры, ограниченной графиками функций
. Найдите площадь фигуры, ограниченной графиками функций 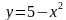 и y = 3 – x .
и y = 3 – x .
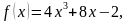 график которой проходит через точку A (1; 3).
график которой проходит через точку A (1; 3). 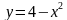 и y = x + 2.
и y = x + 2.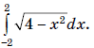

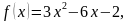 график которой проходит через точку M (1; 4).
график которой проходит через точку M (1; 4). 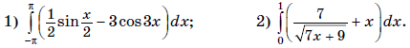
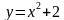 и y = x + 4.
и y = x + 4.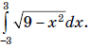








Электронная тетрадь по литературному...
Электронная тетрадь по физике 7 класс...
История России 6 класс ФГОС
Электронная тетрадь по алгебре 7 класс...
Электронная тетрадь по ОБЖ 5 класс ФГОС
Химия 10 класс ФГОС
Электронная тетрадь по истории России 9...
Воспитательные мероприятия для...
© 2020, Коптева Лайсан Мунавировна 55110 1863
Рекомендуем курсы ПК и ППК для учителей