Контрольная работа № 4 по теме «Элементы комбинаторики. Бином Ньютона»
Вариант 1
1. Найдите значение выражения:
1) 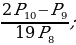 2)
2) 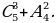
2. В распоряжении командира воинского подразделения есть пять солдат. Сколько у него существует способов направить этих солдат для охраны пяти объектов?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 1, 2, 3, 5 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство 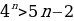 .
.
5. Выражение 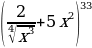 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 29 включительно шесть чисел так, чтобы среди выбранных было ровно два чётных числа?
Вариант 2
1. Найдите значение выражения:
1) 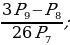 2)
2) 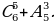
2. Семья из четырёх человек приобрела 4 билета в театр. Сколько существует способов рассадить членов этой семьи на места в соответствии с купленными билетами?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 1, 3, 4, 7 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство 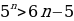 .
.
5. Выражение 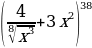 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 25 включительно семь чисел так, чтобы среди выбранных было ровно два чётных числа?
Вариант 3
1. Найдите значение выражения:
1) 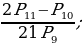 2)
2) 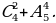
2. Для награждения призёров математической олимпиады в распоряжении жюри есть 5 призов. Сколько существует способов наградить 5 победителей олимпиады?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 2, 3, 5, 7 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство 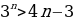 .
.
5. Выражение 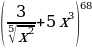 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 33 включительно шесть чисел так, чтобы среди выбранных было ровно два нечётных числа?
Вариант 4
1. Найдите значение выражения:
1) 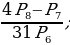 2)
2) 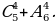
2. Каждую клетку таблицы размером 2 × 2 клетки красят в один из четырёх цветов, причём все четыре цвета должны быть использованы. Сколько существует способов раскраски этой таблицы?
3. Сколько существует чётных трёхзначных чисел, в записи которых используются только цифры 5, 6, 7, 9 (все цифры в записи числа должны быть различны)?
4. Докажите, что при всех n ∈ N выполняется неравенство 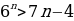 .
.
5. Выражение 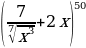 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
6. Сколько существует способов выбрать из натуральных чисел от 1 до 19 пять чисел так, чтобы среди выбранных было ровно два чётных числа?







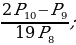 2)
2) 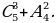
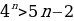 .
. 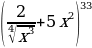 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x? 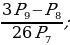 2)
2) 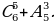
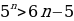 .
.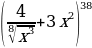 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x? 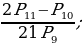 2)
2) 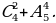
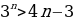 .
. 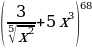 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x? 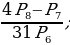 2)
2) 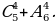
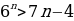 .
.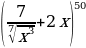 разложили по формуле бинома Ньютона. Какой член разложения не зависит от x?
разложили по формуле бинома Ньютона. Какой член разложения не зависит от x? 


















