Контрольная работа № 4 по теме «Объёмы многогранников»
Вариант 1
1. Основание прямой треугольной призмы – прямоугольный треугольник с катетами 3 см и 10 см. Высота призмы равна 8 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 12 см и образует с плоскостью основания угол 45°.
3. Найдите объём правильной усечённой треугольной пирамиды, стороны оснований которой равны 6 см и 8 см, а высота – 9 см.
4. Основанием пирамиды является равнобедренный треугольник с углом α при основании и радиусом вписанной окружности r. Две боковые грани пирамиды, содержащие боковые стороны основания, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной треугольной пирамиде плоский угол при вершине равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 2
1. Основание прямой четырёхугольной призмы – параллелограмм со сторонами 4 см и 5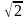 см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы.
см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой образует с плоскостью основания угол 60°, а сторона основания равна 8 см.
3. Найдите объём правильной усечённой четырёхугольной пирамиды, стороны оснований которой равны 4 см и 7 см, а высота – 12 см.
4. Основанием пирамиды является прямоугольный треугольник с катетом a и прилежащим острым углом α. Две боковые грани пирамиды, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной четырёхугольной пирамиде плоский угол при вершине равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 3
1. Основание прямой треугольной призмы – треугольник со сторонами 4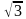 см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы.
см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, апофема которой равна 16 см и образует с плоскостью основания угол 30°.
3. Найдите объём правильной усечённой треугольной пирамиды, стороны оснований которой равны 2 см и 10 см, а высота – 6 см.
4. Основанием пирамиды является прямоугольный треугольник с катетом b и противолежащим острым углом β. Две боковые грани пирамиды, содержащие катеты этого треугольника, перпендикулярны плоскости основания, а третья наклонена к ней под углом α. Найдите объём пирамиды.
5. В правильной четырёхугольной пирамиде угол между боковым ребром и стороной основания равен α. Найдите объём пирамиды, если её высота равна h.
Вариант 4
1. Основание прямой четырёхугольной призмы – прямоугольник со сторонами 4 см и 7 см. Высота призмы равна 3 см. Найдите объём призмы.
2. Найдите объём правильной четырёхугольной пирамиды, боковое ребро которой равно 20 см и образует с высотой пирамиды угол 45°.
3. Найдите объём правильной усечённой четырёхугольной пирамиды, стороны оснований которой равны 3 см и 9 см, а высота – 5 см.
4. Основанием пирамиды является равнобедренный треугольник с радиусом описанной окружности R и углом α при вершине. Две боковые грани пирамиды, содержащие стороны этого угла, перпендикулярны плоскости основания, а третья наклонена к ней под углом β. Найдите объём пирамиды.
5. В правильной треугольной пирамиде угол между боковым ребром и стороной основания, имеющей с ним общую вершину, равен α. Найдите объём пирамиды, если её высота равна h.







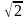 см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы.
см и углом 45° между ними. Высота призмы равна 6 см. Найдите объём призмы. 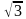 см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы.
см и 6 см и углом 60° между ними. Высота призмы равна 2 см. Найдите объём призмы. 

















