Модуль 9
Испытания Бернулли
Контрольная работа
Работу выполнила: Рыбальченко Т.Н..
Учитель математики МКОУ СОШ с. Малиновка
Решите задачи
Будут ли испытаниями Бернулли следующие серии опытов (если да, то найдите р и q в тех случаях, когда это возможно):
а) десятикратное бросание кубика; успех выпадение шестерки;
б) ответы у доски на уроках математики в течение месяца; успех получение пятерки;
в) проверка лампочек при их продаже в магазине; успех лампочка бракованная;
г) вытаскивание 10 карт из колоды без возвращения; успех вытаскивание красной масти.
Решение.
а) Десятикратное бросание кубика:
Да, это испытания Бернулли, так как каждый бросок кубика независим от предыдущих и имеет только два возможных исхода: успех (выпадение шестерки) или неудача (не выпадение шестерки).
В этом случае вероятность успеха (выпадения шестерки) обозначается как p = 1/6, а вероятность неудачи (не выпадения шестерки) как q = 5/6.
б) Ответы у доски на уроках математики в течение месяца:
Нет, это не испытания Бернулли, так как ответы у доски на уроках математики могут зависеть друг от друга и от общего состояния ученика в определенный момент времени.
в) Проверка лампочек при их продаже в магазине:
Да, это испытания Бернулли, так как каждая лампочка проверяется независимо от других и имеет только два возможных исхода: успех (лампочка бракованная) или неудача (лампочка нормальная).
В этом случае вероятность успеха (лампочка бракованная) обозначается как p, а вероятность неудачи (лампочка нормальная) как q.
г) Вытаскивание 10 карт из колоды без возвращения:
Да, это испытания Бернулли, так как каждое вытаскивание карты происходит независимо от предыдущих и имеет только два возможных исхода: успех (вытаскивание красной масти) или неудача (вытаскивание не красной масти).
В этом случае вероятность успеха (вытаскивание красной масти) обозначается как p, а вероятность неудачи (вытаскивание не красной масти) как q.
Какова вероятность, что при бросании шести кубиков выпадет хотя бы одна шестерка?
Решение.
Обозначим через 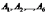 события, состоящие в том, что шестерка выпадает на 1-м, 2-м, …, 6-м кубике соответственно. Тогда интересующее нас событие
события, состоящие в том, что шестерка выпадает на 1-м, 2-м, …, 6-м кубике соответственно. Тогда интересующее нас событие
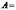 {шестерка выпадет хотя бы на одном из кубиков} можно записать как
{шестерка выпадет хотя бы на одном из кубиков} можно записать как
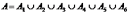 .
.
Поскольку события 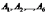 , очевидно, независимы, то
, очевидно, независимы, то
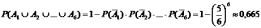
В подъезде горит 5 лампочек. Вероятность, что любая лампочка не сгорит в течение ближайшего месяца, равна 0,2. Какова вероятность, что в течение месяца
а) сгорят все лампочки;
б) сгорит ровно одна лампочка;
в) останутся гореть, по крайней мере, 3 лампочки.
Решение
а) Так как одна лампа перегорает в течении месяца с вероятностью 0,8, то 5 ламп перегорят с вероятностью
Р(А)= 0,8*0,8*0,8*0,8*0,8=0,32768
б) С1из 5*0,8*0,2*0,2*0,2*0,2 =0,064
в) С3 из 5*0,2*0.2 *0,2*0,8*0,8+С4из5*0,2*0,2*0,2*0,2*0,8+0,2*0,2*0,2*0,2*0,2=0,058
Вратарь футбольной команды отражает в среднем каждый третий пенальти. Сколько пенальти из пяти он отразит, скорее всего? С какой вероятностью?
Решение.
Для решения этой задачи мы можем использовать биномиальное распределение.
Вероятность успеха (отражения пенальти) обозначим как p = 1/3, вероятность неудачи (непопадания пенальти) как q = 2/3, количество испытаний (пенальти) n = 5.
Вероятность отражения k пенальти из 5 вычисляется по формуле биномиального распределения:
P(k успехов) = C(n, k) * p^k * q^(n-k)
где C(n, k) - число сочетаний из n по k, равно n! / (k! * (n-k)!)
Теперь найдем вероятность отражения каждого возможного числа пенальти (от 0 до 5) и выберем наиболее вероятное количество:
P(0 успехов) = C(5, 0) * (1/3)^0 * (2/3)^5 ≈ 0.131687
P(1 успех) = C(5, 1) * (1/3)^1 * (2/3)^4 ≈ 0.329218
P(2 успеха) = C(5, 2) * (1/3)^2 * (2/3)^3 ≈ 0.329218
P(3 успеха) = C(5, 3) * (1/3)^3 * (2/3)^2 ≈ 0.164609
P(4 успеха) = C(5, 4) * (1/3)^4 * (2/3)^1 ≈ 0.041152
P(5 успехов) = C(5, 5) * (1/3)^5 * (2/3)^0 ≈ 0.004115
Наиболее вероятное количество отраженных пенальти - 1 или 2 с вероятностью примерно 0.329218 каждый.
Ответ:
Вероятнее всего вратарь отразит 1 или 2 пенальти из пяти с вероятностью около 0.329218 каждый.
Завод отправил заказчику 10000 стандартных изделий. Средняя доля изделий, повреждаемых при транспортировке, составляет 0,02%. Найдите вероятность того, что в этой партии будет повреждено.
а) ровно 3 изделия;
б) не более 3 изделий.
Решение.
1.а) Вероятность того, что изделие будет повреждено при транспортировке, равна р = 0,0002. Так как р – мала, n = 10000 – велико и λ = n*p = 10000*0,0002 = 2≤10, следует применить формулу Пуассона :. P3,10000 = P3(2) = 0,18041.
б) Вероятность P10000(m ≥ 3) может быть вычислена как сумма большого количества слагаемых:P10000(m ≥ 3) = P3,10000+ P4,10000+…+ P10000,10000.Но, разумеется, проще ее найти, перейдя к противоположному событию:P10000(m ≥ 3) = 1 - P10000(m
2.а) В данном случае p = 1-0,0002 = 0,9998 и надо найти P9997,10000, для непосредственного вычисления которой нельзя применить ни формулу Пуассона (р велика), ни локальную формулу Муавра-Лапласа (npq ≈ 2
.2.б) Событие «не будет повреждено хотя бы 9997 из 10000» равносильно событию «будет повреждено не более 3 из 10000», для которого p = 0,0002 иP10000(m ≤ 3) = P0,10000+ P1,10000+ P2,10000+ P3,10000 = 0,1353+0,2707+0,2707+0,1805 = 0,8572.





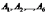 события, состоящие в том, что шестерка выпадает на 1-м, 2-м, …, 6-м кубике соответственно. Тогда интересующее нас событие
события, состоящие в том, что шестерка выпадает на 1-м, 2-м, …, 6-м кубике соответственно. Тогда интересующее нас событие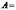 {шестерка выпадет хотя бы на одном из кубиков} можно записать как
{шестерка выпадет хотя бы на одном из кубиков} можно записать как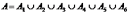 .
.