Конус в природе

Муниципальное автономное общеобразовательное учреждение

«Школа № 1» Камышловского городского округа

Имени Героя Советского Союза Бориса Самуиловича Семёнова

Конус вокруг нас

(исследовательский проект)

Выполнили:

Михайлова Арина

учащаяся 7а класса

МАОУ СОШ №1 КГО

Руководитель:

Тюшева Л.В.,

учитель географии

Камышлов 2019

Содержание:

Введение ………………………………………………………………… 3-4

Глава 1. История изучения геометрического тела конуса……………. 5-9

1.1. Теория Евклида ………………………………………………….. 5-6

1.3. Теория Евдоксиса Книдского…………………………………… 6

1.4. Теория Апполония Перского……………………………………… 6-7

1.5. Теория Архимеда…………………………………………………… 7-9

Глава 2. Конус в природе………………………………………………. 10-11

2.1. Конус в быту ………………………………………………………. 10

2.2. Конусы в архитектуре …………………………………………….. 11

Глава 3. Практическая работа …………………………………………. 12-14

3.1. Социологический опрос ……………………………………………. 12

3.2.

Заключение …………………………………………………………. 13-14

Литература ……………………………………………………………… 15

Приложение ……………………………………………………….. … 16

Введение

Геометрические объекты являются неотъемлемой частью нашей жизни. На уроках геометрии школьники изучают различные геометрические тела, изображают их в тетради, решают задачи. Но очень часто бывает, что выйдя из школы, они не могут применить знания в обыкновенной жизни. Теряется связь с приобретенными знаниями. В связи с этим назрела необходимость исследования объектов в форме конуса в нашем городе, которые позволят наглядно (визуально) представить геометрическое понятие тел, которое будет способствовать качественному освоению материала.

Разработанный материал можно будет использовать c применением интерактивных средств обучения, которые позволят проводить уроки продуктивнее и интереснее. Благодаря наглядности и интерактивности класс вовлекается в активную работу, обостряется восприятие, повышается концентрация внимания, улучшается понимание и запоминание материала

Если оглядеться вокруг - можно заметить, как разнообразен наш Мир (какие предметы нас окружают). Всё это «разнообразие» - геометрические фигуры и тела. Своё место занимают здесь и тела вращения, из которых состоит даже тело человека (шар, цилиндр, конус). Но невозможно, например, построить здание с опорными колоннами в форме цилиндра без каких-либо расчётов (иначе оно обвалится). Отсюда возникает необходимость в изучении составляющих этого здания как геометрических фигур. Среди этого разнообразия геометрических фигур меня заинтересовал конус, который по своим энергетическим свойствам похож на пирамиду.

Цель работы: исследовать, где встречается в природе геометрическое тело конус

Задачи:

1. Изучить литературу по данной проблеме.

2. Составить презентацию.

3. Составить сборник «Конус в природе»

4. Найти примеры в живой и неживой природе, которые демонстрируют геометрическое тело конус в городе Камышлове и его окрестостях.

5. Провести социологический опрос среди 7 классов.

Объект исследования: предметы, имеющие форму конуса

Предмет исследования: геометрическая фигура конус

Методы исследования:

1.  Наблюдение.

2.  Анализ.

3.  Сравнительно – описательный.

4.  Оформление результатов исследования.

Актуальность работы: Если оглядеться вокруг - можно заметить, как разнообразен наш Мир. Всё это «разнообразие» - геометрические фигуры и тела. Своё место занимают здесь и тела вращения, из которых состоит даже тело человека (шар, цилиндр, конус). Но невозможно, например, построить здание с опорными колоннами в форме цилиндра без каких-либо расчётов (иначе оно обвалится). Отсюда возникает необходимость в изучении составляющих этого здания как геометрических фигур.

Методы исследования: наблюдение; сравнение, анализ.

Глава 1. История изучения геометрического тела конуса.

1.1. Теория Евклида.

Первоначальные сведения о свойствах геометрических тел люди нашли, наблюдая окружающий мир и в результате практической деятельности. Со временем ученые заметили, что некоторые свойства геометрических тел можно выводить из других свойств путем рассуждения. Так возникли теоремы и доказательства.

Появилось естественное желание по возможности сократить число тех свойств геометрических тел, которые берутся не­посредственно из опыта. Утверждения, оставшиеся без дока­зательства свойств, стали аксиомами. Таким образом, аксиомы имеют опытное происхождение.

Геометрия в ранний период своего развития достигла особенно высокого уровня в Египте. В первом тысячелетии до нашей эры геометрические сведения от египтян перешли к грекам. За период с VII по III век до нашей эры гре­ческие геометры не только обогатили геометрию многочисленными новыми теоремами, но сделали также серьезные шаги к строгому ее обоснованию. Многовековая работа греческих геометров за этот период была подытожена Евклидом в его знаменитом труде «Начала».

Евклид (330-275гг. до н.э.) Сведения о времени и месте его рождения до нас не дошли, однако известно, что Евклид жил в Александрии и расцвет его деятельности приходится на время царствования в Египте Птолемея I Сотера. Известно также, что Евклид был моложе учеников Платона (427—347 до н. э.), но старше Архимеда (ок. 287—212 до н. э.), так как, с одной стороны, был платоником и хорошо знал философию Платона (именно поэтому он закончил «Начала» изложением т. н. платоновых тел, т. е. пяти правильных многогранников), а с другой стороны — его имя упоминается в первом из двух писем Архимеда к Досифею «О шаре и цилиндре». С именем Евклида связывают становление александрийской математики (геометрической алгебры) как науки.

В XI книге «Начал» дается следующее определение: если вращающийся около одного из своих катетов прямоугольный треугольник слева вернется в то же самое положение, из которого он начал двигаться, то описанная фигура будет конусом.

Неподвижный катет, вокруг которого поворачивается треугольник, называется осью конуса, а круг, описываемый вращающимся катетом, называется основанием конуса. Евклид рассматривает только прямые конусы,

т.е. такие, у которых ось перпендикулярна к основанию, лишь Аполлоний различает прямые и косые конусы, у которых ось образует с основанием угол, отличный от прямого.

В XII книге «Начал» Евклида содержится следующие теоремы.

1. Объём конуса равен одной трети объёма цилиндра с равным основанием и равной высотой; доказательство этой теоремы принадлежит Евдоксу Книдскому.

2. Отношение объёмов двух конусов с равными основаниями равно отношению соответствующих высот.

Если два конуса равновелики, то площади их оснований обратно пропорциональны соответствующим высотам и наоборот.

1.2. Теория Демокрита.

Демокрит  (около 460 до н.э., Абдера, Фракия — около 360 до н.э.), древнегреческий философ, основоположник атомистического учения.

Демокрит был родом из богатой семьи. Согласно передаваемой Диогеном Лаэртием легенде, учился у каких-то магов и халдеев, подаренных персидским царем Ксерксом отцу Демокрита за то, что тот угостил проходившее через Фракию персидское войско обедом. По смерти отца истратил свою часть богатого наследства на путешествия, посетив Персию и Вавилон, Индию и Египет. Некоторое время жил в Афинах, где инкогнито слушал Сократа; возможно, встречался с Анаксагором. Традиционно считается, что наибольшее влияние на Демокрита оказал атомист Левкипп, однако именно с именем Демокрита связывают возникновение атомизма как универсального философского учения, включающего физику и космологию, эпистемологию, психологию и этику; учения, возникшего как синтез проблематики трех древнейших философских школ Греции: милетской, элейской и пифагорейской. Идею атомизма ученый последовательно применял во всех своих исследованиях: в математике, физике, астрономии, биологии, психологии, культуре, политике, логике.

1.3. Теория Евдоксиса Книдского.

Строгое доказательство теорем, служащих для вывода формулы объема конуса и изложенных в пяти предложениях 12 книги “Начал” Евклида, дал Евдоксис Книдский.  В первом из них методом исчерпывания доказывается, что объем конуса равен 1/3 объема цилиндра, имеющего то же основание и ту же высоту. В следующем предложении тем же методом доказывается, что отношение объемов конусов с равными высотами равно отношению площадей их оснований. В третьем из упомянутых предложений доказывается, что объемы 2 подобных конусов, т. е. таких, у которых оси и диаметры оснований пропорциональны, относятся как кубы диаметров. Наконец, в последних 2 предложениях устанавливается, что отношение объемов 2 конусов, площади оснований которых равны, равно отношению высот. По определению Евклида, конус образуется от вращения прямоугольного треугольника, вокруг одного из катетов.

1.4. Теория Апполония Перского.

Апполоний Пергский  (ок.260-ок.170гг до н. э.), древнегреческий математик и астроном, ученик Евклида дал полное изложение теории и основанных им трудов «Конические сечения» в восьми книгах. В зависимости от взаимного расположения конуса и секущей плоскости получают три типа: параболу, эллипс, гиперболу.

У Евклида нет понятия конической поверхности, оно было введено Аполлонием в его “Конических сечениях”, при этом он имел в виду обе плоскости конуса. Вот что пишет Апполоний: «Если от какой-либо точки окружности круга, который не находится в одной плоскости с некоторой точкой, проводить прямые, соединяющие эту точку с окружностью, и при неподвижности точки перемещать прямую по окружности, возвращая ее туда, откуда началось движение, то поверхность, описанную прямой и составленную из 2 поверхностей, лежащих в вершине друг против друга, из которых каждая бесконечно увеличивается, если бесконечно продолжать описывающую прямую, я называю конической поверхностью, неподвижную же точку - её вершиной, а осью - прямую, проведённую через эту точку и центр круга». Определение конической поверхности Аполлония воспроизведено в современных школьных учебниках с существенной заменой круга на любую линию, так называемую направляющую.

1.5. Теория Архимеда.

Архимед  (лат. Archimedes, греч. Архим˜идис) (около 287 до н.э., Сиракузы, Сицилия — 212 до н.э., там же), древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики. Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел. В основополагающих трудах по статике и гидростатике (закон Архимеда) дал образцы применения математики в естествознании и технике. Архимеду принадлежит множество технических изобретений (архимедов винт, определение состава сплавов взвешиванием в воде, системы для поднятия больших тяжестей, военные метательные машины), завоевавших ему необычайную популярность среди современников.

Архимед получил образование у своего отца, астронома и математика Фидия, родственника сиракузского тирана Гиерона II, покровительствовавшего Архимеду. В юности провел несколько лет в культурном крупнейшем центре того времени Александрии Египетской, где познакомился с Эратосфеном. Затем до конца жизни жил в Сиракузах. Во время Второй Пунической войны (218-201), когда Сиракузы были осаждены войском римского полководца Марцелла, Архимед участвовал в обороне города, строил метательные орудия. Военные изобретения ученого (о них рассказывал Плутарх в жизнеописании полководца Марцелла) в течение двух лет помогали сдерживать осаду Сиракуз римлянами. Архимеду приписывается сожжение римского флота направленными через систему вогнутых зеркал солнечными лучами, но это недостоверные сведения. Гений Архимеда вызывал восхищение даже у римлян. Марцелл приказал сохранить ученому жизнь, но при взятии Сиракуз Архимед был убит.

В трактате «О коноидах и сфероидах» Архимед рассматривает шар, эллипсоид, параболоид и гиперболоид вращения и их сегменты и определяет их объемы. В сочинении «О спиралях» исследует свойства кривой, получившей его имя (см. Архимедова спираль) и касательной к ней. В трактате «Измерение круга» Архимед предлагает метод определения числа pi, который использовался до конца 17 в., и указывает две удивительно точные границы числа p: 3 ¹⁰/₇₁

 ¹/₇. В «Псаммите» («Исчисление песчинок») Архимед предлагает систему счисления, позволявшую записывать сверхбольшие числа, что поражало воображение современников. В «Квадратуре параболы» определяет площадь сегмента параболы сначала с помощью «механического» метода, а затем доказывает результаты геометрическим путем. Кроме того, Архимеду принадлежат «Книга лемм», «Стомахион» и обнаруженные только в 20 веке «Метод» (или «Эфод») и «Правильный семиугольник». В «Методе» Архимед описывает процесс открытия в математике, проводя четкое различие между своими механическими приемами и математическим доказательством.

В физике Архимед ввел понятие центра тяжести, установил научные принципы статики и гидростатики, дал образцы применения математических методов в физических исследованиях. Основные положения статики сформулированы в сочинении «О равновесии плоских фигур». Архимед рассматривает сложение параллельных сил, определяет понятие центра тяжести для различных фигур, дает вывод закона рычага. Знаменитый закон гидростатики, вошедший в науку с его именем (смотри Архимеда закон), сформулирован в трактате «О плавающих телах». Существует предание, что идея этого закона посетила Архимеда, когда он принимал ванну; с возгласом «Эврика!» он выскочил из ванны и нагим побежал записывать пришедшую к нему научную истину.

Архимед построил небесную сферу — механический прибор, на котором можно было наблюдать движение планет, Солнца и Луны (описан Цицероном; после гибели Архимеда планетарий был вывезен Марцеллом в Рим, где на протяжении нескольких веков вызывал восхищение); гидравлический орган, упоминаемый Тертуллианом как одно из чудес техники (изобретение органа некоторые приписывают александрийскому инженеру Ктесибию). Считается, что еще в юности, во время пребывания в Александрии, Архимед изобрел водоподъемный механизм (смотри Архимедов винт), который был применен при осушении залитых Нилом земель. Он построил также прибор для определения видимого (углового) диаметра Солнца (о нем Архимед рассказывает в трактате «Псаммит») и определил значение этого угла. Архимеду принадлежит первенство во многих открытиях из области точных наук. До нас дошло тринадцать трактатов Архимеда. В самом знаменитом из них — «О шаре и цилиндре» (в двух книгах) Архимед устанавливает, что площадь поверхности шара в 4 раза больше площади наибольшего его сечения; формулирует соотношение объемов шара и описанного около него цилиндра как 2:3 — открытие, которым он так дорожил, что в завещании просил поставить на своей могиле памятник с изображением цилиндра с вписанным в него шаром и надписью расчета (памятник через полтора века видел Цицерон). В этом же трактате сформулирована аксиома Архимеда (называемая иногда аксиомой Евдокса), играющая важную роль в современной математике.

В «Началах» Евклида мы находим определение только объёмов цилиндра и конуса, площадь же боковых поверхностей была найдена Архимедом. В14-м предложении его произведения «О шаре и цилиндре» он доказал теорему.

Глава 2. Конус вокруг нас

2.1. Применение конуса в быту.

Знания о конусе широко применяются в жизни - в быту, на производстве, в науке. Например, в быту мы часто используем вёдра, имеющие форму усечённого конуса, служащие нам ёмкостью для различных жидкостей и сыпучих веществ. Наши растения, благоприятно развиваются в цветочных горшках. А эти предметы чаще всего имеют форму либо прямого кругового конуса, либо форму усечённого конуса.

Для переливания жидкостей из более крупной посуды, в более мелкую мы используем воронку. Если присмотреться к её форме, мы заметим, что она похожа на усечённый конус.

Идя по улице, мы можем увидеть человека с интересным приспособлением в руках. Это рупор. Он служит для усиления звука, то есть он является громкоговорителем.

Многие музыкальные инструменты имеют конические элементы. Например, карнай среднеазиатский, зурна армянская, продольная флейта. А если мы вспомним древнего музыканта, который однажды подул в кость, и превратил её в духовный инструмент. Назовём его флейтой, гобоем, кларнетом, дудкой, фаготом. Это деревянные духовные инструменты. Но есть так же группа медных духовных – валторна, труба, тромбон, туба и их разновидности.

В жизни мы нередко встречаемся с конусами. Лампа с металлическим абажуром отбрасывает пучок света в виде конуса. Причём если абажур не расположен параллельно к земле, то конус не будет являться круговым. Его основание образует вытянутая фигура, называемая эллипсом. Если из круга вырезать сектор, а затем склеить его, получиться конус. [6]

Одной из самых распространённых канцелярских принадлежностей является ручка. Она имеет конический элемент на конце. Этим элементом является зауженный конец ручки. (См. прил.5)

Почему пожарное ведро имеет форму конуса? (См. прил. 8)

Конусовидная форма пожарных ведер обусловлена следующими причинами: с производственной точки зрения:

1. Такая форма позволяет не припаивать днище, следовательно, производственный процесс заметно упрощается.

2. С бытовой точки зрения: - Такое ведро не украдут с пожарного щита, для бытового использования оно не пригодно.

3. С точки зрения пожарной науки такая форма ведра позволяет быстро справиться с возгоранием: - Во-первых, конусовидная форма ведра позволяет в зимнее время пробивать лунки в пожарных водоемах; - Во-вторых, особая форма пожарного ведра позволяет избежать расплескивания воды при тушении. Из обычного ведра вода выливается не равномерно, а из пожарного ведра вода выливается целенаправленной струей. Его невозможно поставить на землю так, чтобы оно не упало. Так же коническая форма сделана для того, чтобы даже при падении пожарного бойца вода вылилась на огонь. 

2.2. Применение конуса в архитектуре

При построении различных зданий и сооружений очень требуются познания в области геометрии, а особенно в таком её разделе, как стереометрия. А, в свою очередь, рассматриваемая нами, фигура относится именно к этому разделу.

Очень часто мы встречаем конус в элементах архитектуры. Ярким примером этого наблюдения является конус, который лежит в основании крыш домов. Я хотела бы проиллюстрировать мои наблюдения. (См. прил. 2,4 )

2.3. Конус в природе

Многие предметы живой и неживой природы имеют форму конуса.

(См. прил 1, 3, 6 )

Глава 3. Практическая часть

3.1. Проведение социологического опроса.

Цель: что знают учащиеся 7а класса о конусе в природе

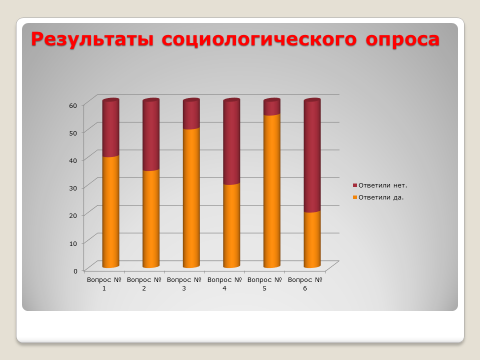
Социологический опрос был проведен 25 ноября 2018 года. В опросе участвовали 30 семиклассников нашей школы. Им было предложено ответить на 6 вопросов. (См. пррил. )

Мы проанализировали результаты опроса и их представили в диаграмме.

3.2. Выявление предметов живой и не живой природы в форме конуса в городе Камышлове и его окрестностях.

Мы прошли по улицам Камышлова и увидели предметы в форме конуса:

ели на площади, на зданиях мы увидели элементы архитектуры в виде конуса.

Дома мы нашли предметы, имеющие форму конуса: посуда, воронка, цветочные горшки, ручка……

Заключение

При подготовке к этой работе я узнала много нового о геометрической фигуре конус. Например, я стала внимательнее относиться к предметам, окружающим нас в повседневной жизни. Я обнаружила, что вокруг очень много различных геометрических фигур, в том числе и конус. Он очень широко применяется нами в быту. Так же мы часто сталкиваемся с этой геометрической фигурой в природе. Она широко применяется в промышленности, так как большинство ёмкостей для растворов имеет конусовидную форму.

Если мы пройдёмся по улице какого-либо города, то, наверняка, заметим, что элементы конуса встречаются в архитектуре. Примером этого служат крыши различных зданий и сооружений, где мы с лёгкостью можем увидеть конус.

Так же знания о конусе и его элементов иногда очень требуется в жизни. Например, при подсчёте объёма жидкости, находящейся в ведре, которое имеет форму прямого кругового конуса или усечённого конуса.

Проведенная поисково-исследовательская работа позволила нам расширить и приобрести дополнительные знания о геометрическом теле - конус.

Теперь мы стали внимательнее относиться к окружающим меня предметам, разнообразие которых влияет на наше настроение и эмоции.

Источники

1. Геометрические тела. Конус.- [Электронный ресурс]. - Режим доступа. - www.calc.ru/Geometricheskiye-Tela-Konus.html

2. Конус.- [Электронный ресурс]. - Режим доступа.- www.tutoronline.ru

3. Погорелов М.И «Геометрия 7-11» Просвещение 2001.

4. Геометрия в таблицах. 7-11 классы. Нелин Е.П.,  М.: 2012.— 80 с. 

5. ФИПИ www.fipi.ru/content/otkrytyy-bank-zadaniy-ege

6. «Что такое? Кто такой?» Дрофа 2005 стр. 283-285

7. «Что такое? Кто такой?» Дрофа 2005 стр. 309-313

Приложение 1

Конус в природе

Песчаные холмы Сахары

Приложение 2

Конус в архитектуре

Приложение 3

Космическое пространство

Приложение 4

Цветочные композиции

Приложение 5

Конус в быту

р упор

КРАТЕР ВУЛКАНА

Приложение 6

ШИШКИ

Морские раковины

Гриб

Приложение 7

Вопросы социологического опроса

Приложение 8

Результаты социологического опроса

п риложение 8

Пожарное ведро

16