Копилка нестандартных задач по математике

Копилка нестандартных задач по математике

Ивановский железнодорожный колледж

Выполнила Зубкова Ксения Группа 5/6

Руководитель: Савенко Ирина Николаевна.

2020 год

Нестандартная задача – это задача, алгоритм решения которой решающему неизвестен.

Решение нестандартных задач включает следующие этапы: 

• 1) анализ текста задачи (усвоение содержания); 
• 2) поиск решения (разбор задачи и составление плана решения); 
• 3) осуществление плана решения; 
• 4) проверка решения задачи. 

Нестандартные задачи развивают математическое мышление: краткость речи, правильное применение математической терминологии, умение делать доступные выводы и обобщения, обосновывать свои мысли.

Виды нестандартных задач 1. Задачи на смекалку

Пример:  Масса цапли, стоящей на одной ноге 12 кг. Сколько будет весить цапля, если встанет на 2 ноги?

Решение: Вес цапли не изменится. Стоя на двух или одной ноге, весить она всегда будет одинаково. 

Ответ: 12 кг

Виды нестандартных задач

  2. Занимательные задачи

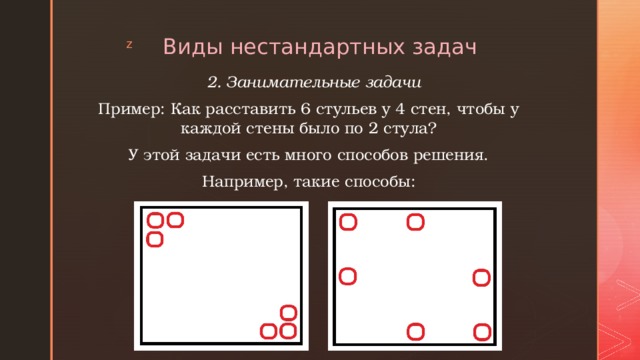
Пример:  Как расставить 6 стульев у 4 стен, чтобы у каждой стены было по 2 стула?

У этой задачи есть много способов решения.

Например, такие способы:

Виды нестандартных задач 3. Логические задачи

Пример:  Среди футбольных мячей красный мяч тяжелее коричневого, а коричневый тяжелее зеленого. Какой мяч тяжелее: зеленый или красный?  

Решение: Если оба мяча сравнить с коричневым, то красный мяч тяжелее коричневого, а зелёный легче коричневого. Значит, красный мяч тяжелее зелёного. 

Ответ: Красный

Виды нестандартных задач 4. Задачи на переливание

Пример:  Бидон, ёмкость которого 10 литров, наполнен соком. Имеются еще пустые сосуды в 7 и 2 литров. Как разлить сок в два сосуда по 5 литров каждый?

Решение: Из бидона 10 л переливаем в сосуд 7 л. Оттуда переливаем в 2 л. В сосуде с 7 л остаётся 5 л. Из 2 л. переливаем в 10 л, где осталось 3 л.

Виды нестандартных задач 5. Комбинаторные задачи

Пример:  У Даши 2 юбки: красная и синяя, и 2 блузки: в полоску и в горошек. Сколько разных нарядов у Даши?

Решение: Даша может выбрать юбку 2 способами, блузку тоже 2, тогда в паре Даша может выбрать 2*2=4 наряда. 

Ответ: 4 наряда

Виды нестандартных задач 6. Геометрические задачи

Пример:  Разрежьте треугольник на два треугольника, четырехугольник и пятиугольник, проведя две прямые линии.

Решение: У этой задачи также много способов решения.

Например, можно решить так:

Виды нестандартных задач 7. Логические квадраты

Пример:  В квадрате (3х3) нужно разместить числа 1, 1, 1, 2, 2, 2, 3, 3, 3 так, чтобы по всем линиям получить в сумме число 6.

Решение:

Методы решения нестандартных задач

Метод перебора

Арифметический метод

Алгебраический метод

Метод предположения

Метод рассуждений

Практический метод

Таким образом, решение различного рода нестандартных логических задач способствует математическому, логическому и осознанному исследованию явлений реального мира.