Сценарий урока в 11 классе по теме:
« Корень n-й степени из действительного числа. »
Цель урока: Формирование у учащихся целостного представления о корне n-ой степени и арифметического корень n-ой степени, формирование вычислительных навыков, навыков сознательного и рационального использования свойств корня при решении различных задач, содержащих радикал. Проверить уровень усвоения учащимися вопросов темы.
Предметные: создать содержательные и организационные условия для усвоения материала по теме «Числовые и буквенные выражения» на уровне восприятия осмысления и первичного запоминания; формировать умения применять данные сведения при вычислении корня n-й степени из действительного числа;
Метопредметные: способствовать развитию вычислительных навыков; умение анализировать, сравнивать, обобщать, делать выводы;
Личностные: воспитывать умение высказывать свою точку зрения, слушать ответы других, принимать участие в диалоге, формировать способность к позитивному сотрудничеству.
Планируемый результат.
Предметные: уметь в процессе реальной ситуации применять свойства корня n-й степени из действительного числа при вычислении корней, решении уравнений.
Личностные: формировать внимательность и аккуратность в вычислениях, требовательное отношение к себе и к своей работе, воспитывать чувство взаимопомощи.
Тип урока: урок изучения и первичного закрепления новых знаний
Мотивация к учебной деятельности:
Восточная мудрость гласит: «Можно коня привести к воде, но нельзя заставить его пить». И человека невозможно заставить учиться хорошо, если он сам не старается узнать больше, не имеет желания работать над своим умственным развитием. Ведь знания только тогда знания, когда они приобретены усилиями своей мысли, а не одной памятью.
Наш урок пройдёт под девизом: «Покорим любую вершину, если будем к ней стремиться». Нам с вами в течение урока нужно успеть преодолеть несколько вершин, и каждый из вас должен вложить все свои усилия, чтобы покорить эти вершины.
«Сегодня у нас урок, на котором мы должны познакомиться с новым понятием: « Корень n-й степени» и научиться применять это понятие к преобразованию различных выражений.
Ваша цель – на основе различных форм работы активизировать имеющиеся знания, внести свой вклад в изучение материала и получить хорошие оценки»
Корень квадратный из действительного числа мы с вами изучали в 8 классе. Корень квадратный связан с функцией вида y=x2. Ребята, вы помните, как мы вычисляли корни квадратные, и какие у него были свойства?
а) индивидуальный опрос: 

что это за выражение
что называется квадратным корнем
что называется арифметическим квадратным корнем
перечислите свойства квадратного корня
б) работа в парах: вычислите.
-
- 

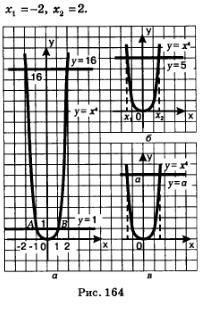
2. Актуализация знаний и создание проблемной ситуации: Решите уравнение x4 =1 . Как мы его можем решить? (Аналитически и графически). Решим его графически. Для этого в одной системе координат построим график функции у = х4 прямую у = 1 (рис. 164 а). Они пересекаются в двух точках: А (-1;1) и B(1;1). Абсциссы точек А и B, т.е. х1= -1,
х2 = 1, являются корнями уравнения х4 = 1.
Рассуждая точно так же, находим корни уравнения х4 =16: А теперь попробуем решить уравнение х4 =5; геометрическая иллюстрация представлена на рис. 164 б. Ясно, что уравнение имеет два корня x1 и x2, причем эти числа, как и в двух предыдущих случаях, взаимно противоположны. Но для первых двух уравнений корни были найдены без труда (их можно было найти и не пользуясь графиками), а с уравнением х4 =5 имеются проблемы: по чертежу мы не можем указать значения корней, а можем только установить, что один корень располагается левее точки -1, а второй — правее точки 1.
Выход из ситуации: Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке. Они ввели в рассмотрение новый символ который назвали корнем четвертой степени, и с помощью этого символа корни уравнения х4 = 5 записали так: х1=  ,
,
х2 = -  (читается: «корень четвертой степени из пяти»).
(читается: «корень четвертой степени из пяти»).
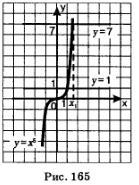
Мы говорили об уравнении х4 = а, где а 0. С равным успехом мы могли говорить и об уравнении х4 =а, где а 0, а n — любое натуральное число. Например, решая графически уравнение х5 = 1, находим х = 1 (рис. 165); решая уравнение х5' = 7, устанавливаем, что уравнение имеет один корень х1, который располагается на оси х чуть правее точки 1 (см. рис. 165). Для числа х1 введем обозначение  .
.
Работа с учебником: Вообще, решая уравнение хn =а, где а 0, n € N, n1, получаем в случае четного n два корня:  (рис. 164, в); в случае нечетного n — один корень
(рис. 164, в); в случае нечетного n — один корень  (читается: «корень n-й степени из числа а ). Решая уравнение хn =0, получаем единственный корень х=0.
(читается: «корень n-й степени из числа а ). Решая уравнение хn =0, получаем единственный корень х=0.
Определение 1. Корнем n-й степени из неотрицательного числа а (n = 2, 3,4, 5,...) называют такое неотрицательное число, которое при возведении в степень n дает в результате число а.
Это число обозначают  , число а при этом называют подкоренным числом, а число n — показателем корня.
, число а при этом называют подкоренным числом, а число n — показателем корня.
Если n=2, то обычно не говорят «корень второй степени», а говорят "«корень квадратный». В этом случае не пишут  Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса.
Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса.
Если n = 3, то вместо «корень третьей степени» часто говорят «корень кубический». Первое знакомство с кубическим корнем у вас также состоялось в курсе алгебры 8-го класса. Мы использовали кубический корень в курсе алгебры 9-го класса.
Итак, если а ≥0, n= 2,3,4,5,…, то 1)  ≥ 0; 2) (
≥ 0; 2) (  )n = а.
)n = а.
Вообще,  =b и bn=а - одна и та же зависимость между неотрицательными числами а и b, но только вторая описана более простым языком (использует более простые символы), чем первая.
=b и bn=а - одна и та же зависимость между неотрицательными числами а и b, но только вторая описана более простым языком (использует более простые символы), чем первая.
Операцию нахождения корня из неотрицательного числа называют обычно извлечением корня. Эта операция является обратной по отношению к возведению в соответствующую степень. Сравните:

Еще раз обратите внимание: в таблице фигурируют только положительные числа, поскольку это оговорено в определении 1. И хотя, например, (-6)6 =36 — верное равенство, перейти от него к записи с использованием квадратного корня, т.е. написать, что  нельзя. По определению
нельзя. По определению  - положительное число, значит
- положительное число, значит  = 6 ( а не -6). Точно так же, хотя и 24=16, т (-2)4=16, переходя к знакам корней, мы должны написать
= 6 ( а не -6). Точно так же, хотя и 24=16, т (-2)4=16, переходя к знакам корней, мы должны написать  = 2 (и в то же время
= 2 (и в то же время  ≠-2).
≠-2).
Иногда выражение  называют радикалом (от латинского слова гаdix — «корень»). В русском языке термин радикальный используется довольно часто, например, «радикальные изменения» — это значит «коренные изменения». Между прочим, и само обозначение корня напоминает о слове гаdix: символ — это стилизованная буква r.
называют радикалом (от латинского слова гаdix — «корень»). В русском языке термин радикальный используется довольно часто, например, «радикальные изменения» — это значит «коренные изменения». Между прочим, и само обозначение корня напоминает о слове гаdix: символ — это стилизованная буква r.
Операцию извлечения корня определяют и для отрицательного подкоренного числа, но только в случае нечетного показателя корня. Иными словами, равенство (-2)5 = -32 можно переписать в эквивалентной форме как  =-2. При этом используется следующее определение.
=-2. При этом используется следующее определение.
Определение 2. Корнем нечетной степени n из отрицательного числа а (n = 3,5,...) называют такое отрицательное число, которое, будучи возведено в степень n, дает в результате число а.
Это число, как и в определении 1, обозначают  , число а — подкоренное число, число n — показатель корня.
, число а — подкоренное число, число n — показатель корня.
Итак, если а  , n=,5,7,…,то: 1)
, n=,5,7,…,то: 1)  0; 2) (
0; 2) (  )n = а.
)n = а.
Таким образом, корень четной степени имеет смысл (т.е. определен ) только для неотрицательного подкоренного выражения; корень нечетной степени имеет смысл для любого подкоренного выражения.
5. Первичное закрепление знаний:
1. Вычислить: № № 33.5; 33.6; 33.74 33.8 устно а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
г) В отличие от предыдущих примеров мы не можем указать точное значение числа  Ясно лишь, что оно больше, чем 2, но меньше, чем 3, поскольку 24=16 (это меньше, чем 17), а З4 = 81 (это больше, чем 17). Замечаем, что 24 намного ближе к 17, чем З4, так что есть основания использовать знак приближенного равенства:
Ясно лишь, что оно больше, чем 2, но меньше, чем 3, поскольку 24=16 (это меньше, чем 17), а З4 = 81 (это больше, чем 17). Замечаем, что 24 намного ближе к 17, чем З4, так что есть основания использовать знак приближенного равенства:
2. Найти значения следующих выражений.
|  = 5 = 5
| Р |  = = 
| Д |
|  = 30 = 30
| Е |  = 30 = 30
| Е |
|  *4 = 2,8 *4 = 2,8
| Н |  = 6 = 6
| К |
|  = 30 = 30
| Е |  = 0,5 = 0,5
| А |
|
|
|  = 5 = 5
| Р |
|
|
|  = 7 = 7
| Т |
Поставить около примера соответствующую букву.
| 5 | 2,8 | 7 | 6 | 
| 0,5 | 30 |
| Р | Н | Т | К | Д | А | Е |
Небольшая информация о великом учёном. Рене Декарт (1596-1650) французский дворянин, математик, философ, физиолог, мыслитель. Рене Декарт заложил основы аналитической геометрии, ввел буквенные обозначения x2, y3. Всем известны декартовы координаты, определяющие функцию переменной величины.
3. Решить уравнения: а)  = -2; б)
= -2; б)  = 1; в)
= 1; в)  = -4
= -4
Решение: а) Если  = -2, то y = -8. Фактически обе части заданного уравнения мы должны возвести в куб. Получим: 3х+4= - 8; 3х= -12; х = -4. б) Рассуждая, как в примере а), возведем обе части уравнения в четвертую степень. Получим: х=1.
= -2, то y = -8. Фактически обе части заданного уравнения мы должны возвести в куб. Получим: 3х+4= - 8; 3х= -12; х = -4. б) Рассуждая, как в примере а), возведем обе части уравнения в четвертую степень. Получим: х=1.
в) Здесь не надо возводить в четвертую степень, это уравнение не имеет решений. Почему? Потому, что согласно определению 1 корень четной степени — неотрицательное число.
Вашему вниманию предложено несколько заданий. Когда вы выполните эти задания, вы узнаете имя и фамилию великого учёного-математика. Этот учёный в 1637 г первым ввел знак корня.
6. Давайте немного отдохнём.
Поднимает руки класс — это «раз».
Повернулась голова – это «два».
Руки вниз, вперёд смотри – это «три».
Руки в стороны пошире развернули на «четыре»,
С силой их к рукам прижать –это «пять».
Всем ребятам надо сесть –это «шесть».
7. Самостоятельная работа:
вариант: 2 вариант:
Вычислите: а)
а)  -
-  ; а)
; а)  +
+  ;
;
б) 3 -
- . б)12 -6
. б)12 -6  .
.
2. Решите уравнение: а) х4= -16; б) 0,02х6-1,28=0; а) х8= -3; б)0,3х9 – 2,4=0;
в)  = -2; в)
= -2; в) = 2
= 2
8. Повторение: Найдите корень уравнения  = - х. Если уравнение имеет более одного корня, в ответ впишите меньший из корней.
= - х. Если уравнение имеет более одного корня, в ответ впишите меньший из корней.
9. Рефлексия : Чему вы научились на уроке? Что было интересным? Что было трудным?
Что легким? Почему?
10. д/з п.33 №№ 33.14-33.15





 ,
,
 .
.  (рис. 164, в); в случае нечетного n — один корень
(рис. 164, в); в случае нечетного n — один корень  (читается: «корень n-й степени из числа а ). Решая уравнение хn =0, получаем единственный корень х=0.
(читается: «корень n-й степени из числа а ). Решая уравнение хn =0, получаем единственный корень х=0.  Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса.
Это тот частный случай, который вы специально изучали в курсе алгебры 8-го класса. 

 нельзя. По определению
нельзя. По определению  - положительное число, значит
- положительное число, значит  = 2 (и в то же время
= 2 (и в то же время  =-2. При этом используется следующее определение.
=-2. При этом используется следующее определение. 









