Тема урока. Корень n-ой степени.
Цель урока: актуализировать знания по теме «Квадратные корни»;
формировать понятие корня n-ой степени;
изучение его свойств, развитие практических навыков.
Тип урока: усвоение новых знаний.
Структура урока:
Организационный момент
Устный счет
Изучение нового материала
Закрепление новых знаний и умений учащихся
Задание на дом
Итог урока
Оборудование: мультимедийный проектор, интерактивная доска, презентация
Ход урока
I. Организационный момент
Сообщение темы и цели урока.
II. Устный счет
Для устного счета задания взяты из банка заданий ОГЭ.
Индивидуальная работа у доски.
Задание 1. Найдите корни уравнения 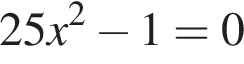
Задание 2. Найдите значение выражения 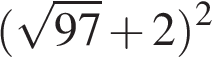
Задание 3. Между какими соседними числами находится 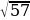 ?
?
Работа с классом.
По графику квадратичной функции сравнить с нулем коэффициенты а и с.
а) 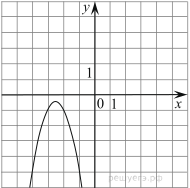 Ответ: а
Ответ: а 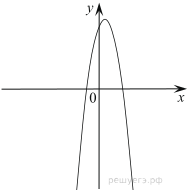 Ответ: а0.
Ответ: а0.
в) 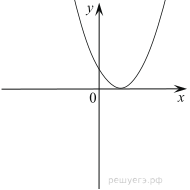 Ответ: а0, в0. г)
Ответ: а0, в0. г) 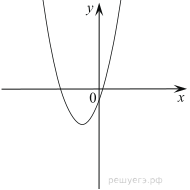 Ответ: а0, в
Ответ: а0, в
III. Изучение нового материала
Определение. Корнем n-ой степени из числа a называют такое число, n-ая степень которого равна a. Этот корень обозначают символом 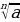 .
.
Пример 1
а) 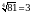 , т.к.
, т.к. 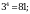 б)
б) 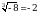 ; т.к.
; т.к. 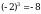 ; в)
; в) 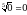 , т.к.
, т.к. 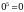 .
.
Принято корень второй степени называть квадратным корнем, корень третьей степени - кубическим корнем.
Уточним понятие корня. Сначала рассмотрим степенную функцию xn = a с нечетным показателем n. Например х3 = a, х5 = a и т.д.
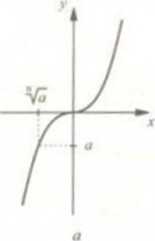 Нечетное
Нечетное
xn = a имеет единственное решение х = 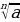 .
.
xn = a с четным показателем n. Например х2 = a, х4 = a и т.д.
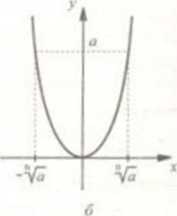 Четное
Четное
Тогда уравнение xn = a при a 0 имеет два противоположных по знаку решения. В этом случае положительное решение обозначают символом 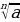 .
.
Пример 2
х4 = 81.:
х1 = 3 и х2 = -3, т.к. при подставленные этих чисел в уравнение получаем верное равенство.
Итак, выражение 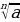 при a 0 имеет смысл при четном и нечетном n, и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем n-й степени из a. Арифметическим корнем n-й степени из неотрицательного числа a называют такое неотрицательное число, n-я степень которого равна a.
при a 0 имеет смысл при четном и нечетном n, и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем n-й степени из a. Арифметическим корнем n-й степени из неотрицательного числа a называют такое неотрицательное число, n-я степень которого равна a.
Корень нечетной степени из отрицательного числа можно выразить через арифметический корень из положительного числа.
Пример 3
Получаем 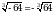 , т. к.
, т. к. 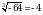 и
и 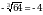 . (Презентация: слайд 11, 12)
. (Презентация: слайд 11, 12)
Свойства корня n-й степени:
1. (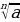 )n = a
)n = a
2. 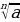 m = (
m = (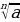 )m
)m
3. 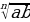 =
= 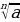
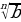
4. 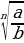 =
= 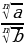
5. 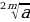 2m = |a|
2m = |a|
В равенствах 1-5 числа m и n – натуральные, в равенствах 1-4 числа a, b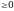 и в равенстве 4 число
и в равенстве 4 число 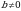 . (Презентация: слайд 13)
. (Презентация: слайд 13)
Пример 4
Вычислим, используя приведенные свойства.
а) 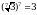 ;
;
б) 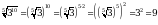 ;
;
в) 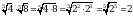 ;
;
г) 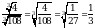 ;
;
д) 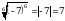 ;
;
IV. Закрепление новых знаний и умений учащихся
Решение упражнений
1)а) 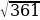 = 19, т.к. 192 = 19 19 = 361
= 19, т.к. 192 = 19 19 = 361
г) 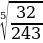 =
= 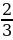 , т.к.(
, т.к.( 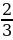 )5 =
)5 = 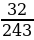
ж) 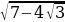 = 2 -
= 2 - 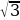 , т.к. (2 -
, т.к. (2 - 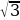 )2 = 4 - 4
)2 = 4 - 4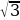 + 3 = 7 -
+ 3 = 7 - 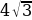 .
.
2)
г) 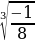 = -
= - 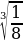 = -
= - 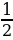
д) 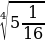 =
= 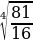 =
= 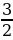
е) 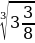 =
= 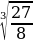 =
= 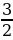
3)
у = 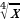
Е (81; 3), 3 = 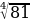 принадлежит
принадлежит
F (81; - 3), - 3 = 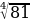 принадлежит
принадлежит
К (- 16; - 2), - 2 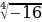 не принадлежит
не принадлежит
L (0,0001; 0,1), 0,1 = 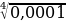 принадлежит
принадлежит
4)
а) 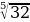 +
+ 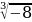 = 2 – 2 = 0
= 2 – 2 = 0
б) 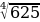 -
- 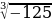 = 5 + 5 = 10
= 5 + 5 = 10
в) (- 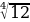 )4 = 12
)4 = 12
г) (2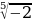 )5 = 32 (-2) = - 64
)5 = 32 (-2) = - 64
д) (3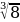 )3 = 27 8 = 216
)3 = 27 8 = 216
V. Задание на дом
Учебник, знать определение и свойства арифметического корня n-й степени.
Задание учителя
VI. Итог урока






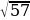 ?
?  Ответ: а
Ответ: а  Ответ: а0.
Ответ: а0. Ответ: а0, в0. г)
Ответ: а0, в0. г)  Ответ: а0, в
Ответ: а0, в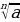 .
. 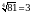 , т.к.
, т.к. 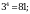 б)
б) 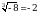 ; т.к.
; т.к. 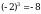 ; в)
; в) 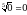 , т.к.
, т.к. 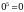 .
. Нечетное
Нечетное Четное
Четное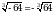 , т. к.
, т. к. 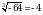 и
и 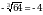 . (Презентация: слайд 11, 12)
. (Презентация: слайд 11, 12)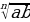 =
= 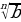
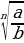 =
= 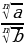
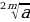 2m = |a|
2m = |a|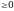 и в равенстве 4 число
и в равенстве 4 число 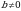 . (Презентация: слайд 13)
. (Презентация: слайд 13)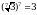 ;
;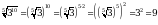 ;
;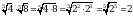 ;
;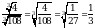 ;
;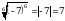 ;
;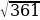 = 19, т.к. 192 = 19 19 = 361
= 19, т.к. 192 = 19 19 = 361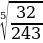 =
= 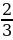 , т.к.(
, т.к.( 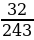
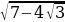 = 2 -
= 2 - 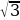 , т.к. (2 -
, т.к. (2 - 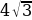 .
.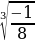 = -
= - 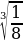 = -
= - 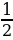
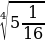 =
= 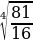 =
= 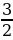
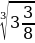 =
= 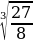 =
= 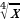
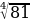 принадлежит
принадлежит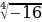 не принадлежит
не принадлежит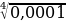 принадлежит
принадлежит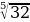 +
+ 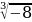 = 2 – 2 = 0
= 2 – 2 = 0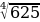 -
- 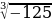 = 5 + 5 = 10
= 5 + 5 = 10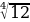 )4 = 12
)4 = 12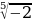 )5 = 32 (-2) = - 64
)5 = 32 (-2) = - 64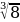 )3 = 27 8 = 216
)3 = 27 8 = 216









