Просмотр содержимого документа
«Итоговая контрольная работа НН»
Г- 9 Итоговая контрольная работа
Вариант 1
1. В треугольнике АВС точка D – середина стороны АВ, точка М – точка пересечения медиан.
а) Выразите вектор  через векторы
через векторы 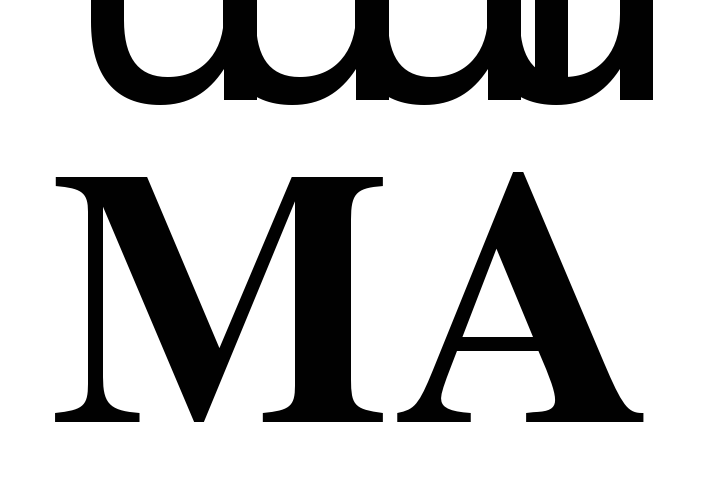 и
и 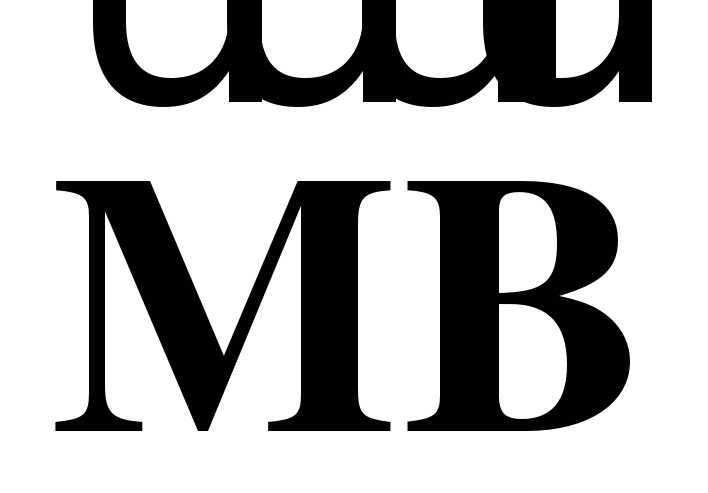 и вектор
и вектор 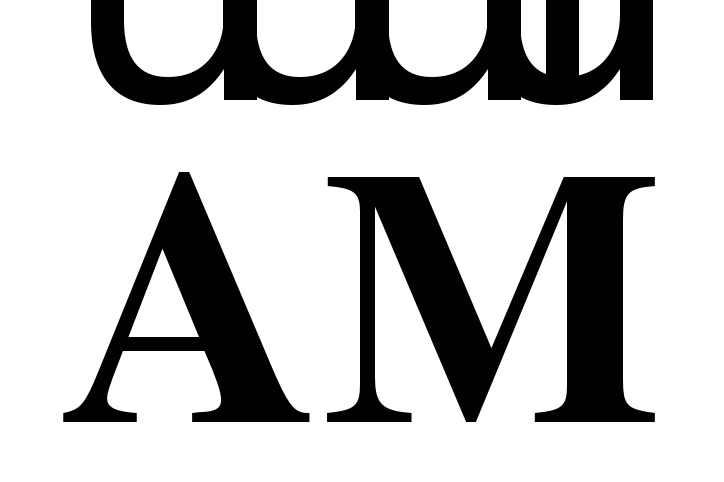 через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение  , если
, если 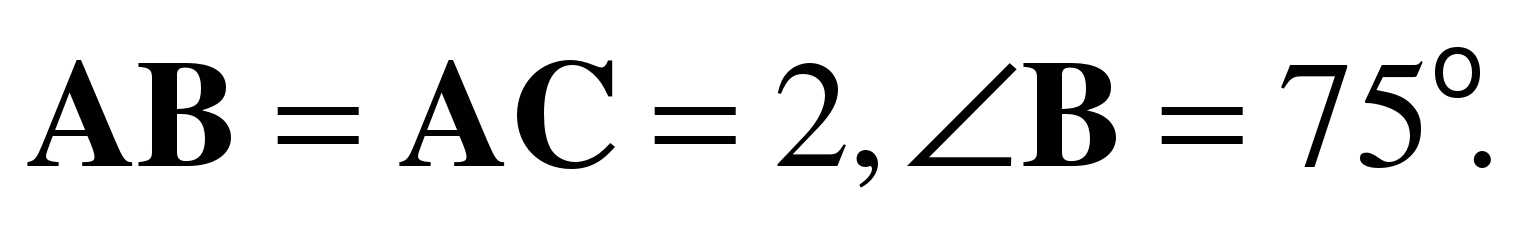
2. Даны точки А(1; 1), В(4; 5), С(-3; 4).
а) Докажите, что треугольник АВС равнобедренный и прямоугольный.
б) Найдите длину медианы СМ.
3. В треугольнике АВС 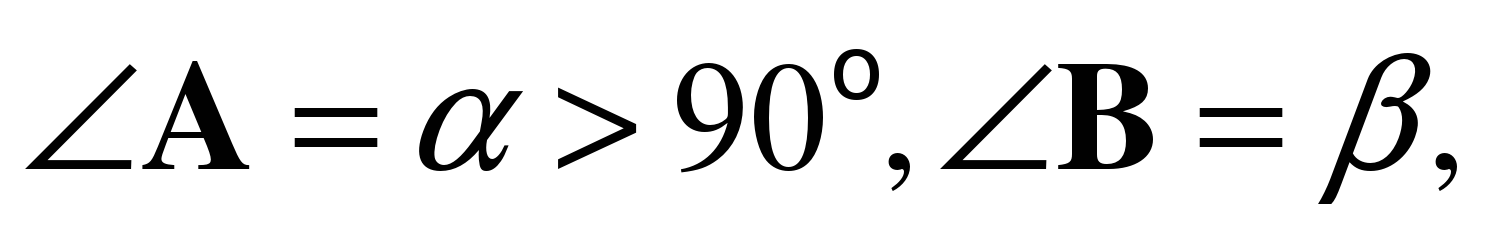 высота ВD равна h.
высота ВD равна h.
а) Найдите сторону АС и радиус R описанной окружности.
б) Вычислите значение R, если 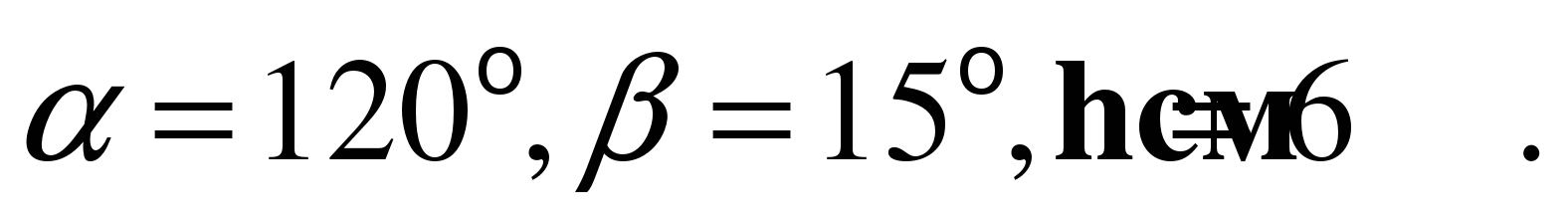
4. Хорда окружности равна а и стягивает дугу в 120о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Итоговая контрольная работа
Вариант 2
1. В параллелограмме АВСD диагонали пересекаются в точке О.
а) Выразите вектор 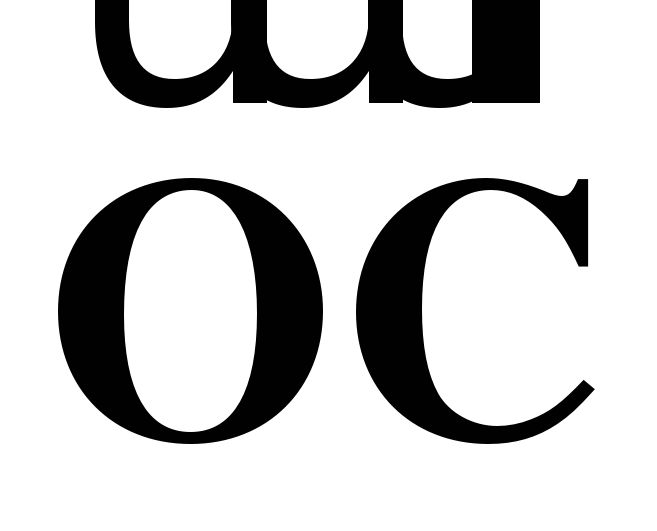 через векторы
через векторы  и
и 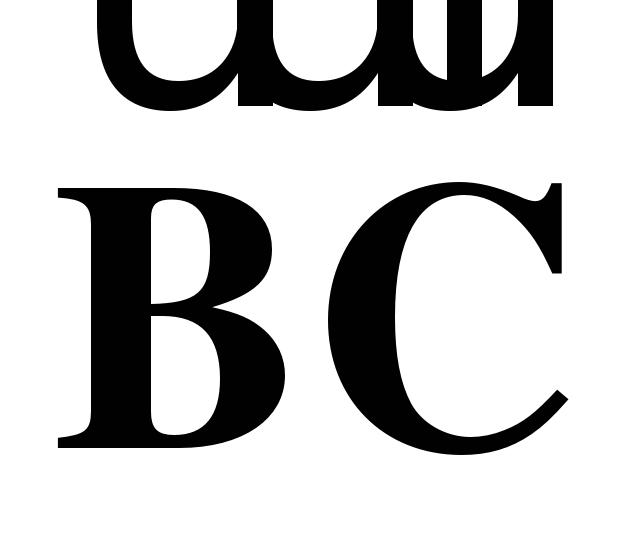 и вектор
и вектор 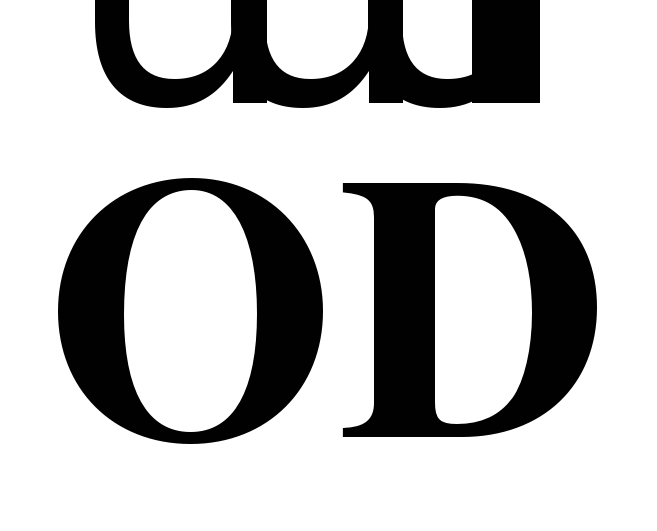 через векторы
через векторы  и
и  .
.
б) Найдите скалярное произведение 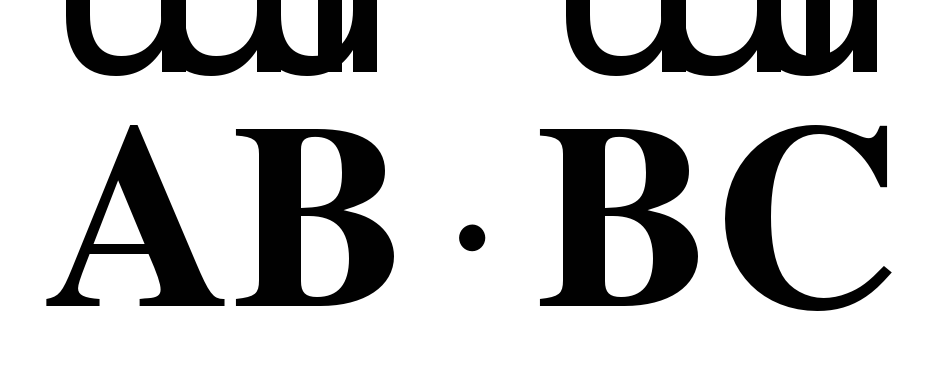 , если
, если 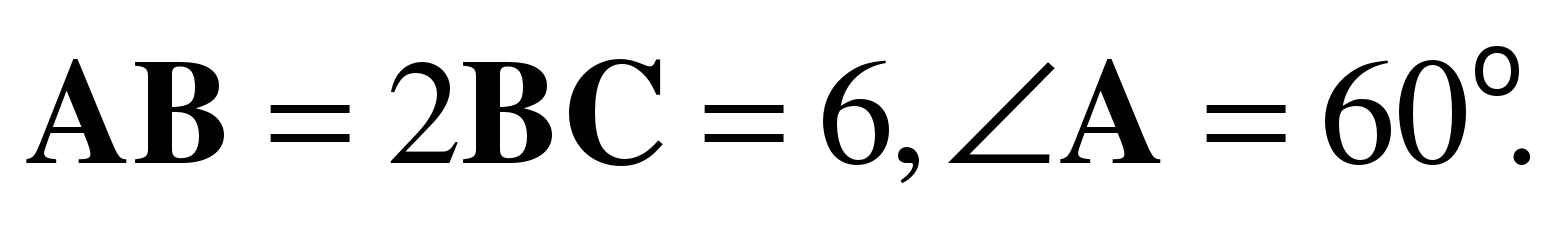
2. Даны точки К(0; 1), М(-3; -3), N(1; -6).
а) Докажите, что треугольник KMN равнобедренный и прямоугольный.
б) Найдите длину медианы NL.
3. В треугольнике АВС 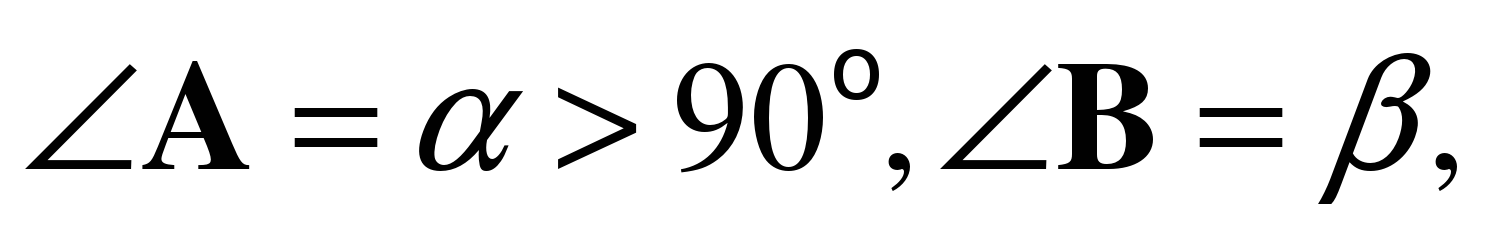 высота ВD равна h.
высота ВD равна h.
а) Найдите сторону АD и радиус R описанной окружности.
б) Вычислите значение R, если 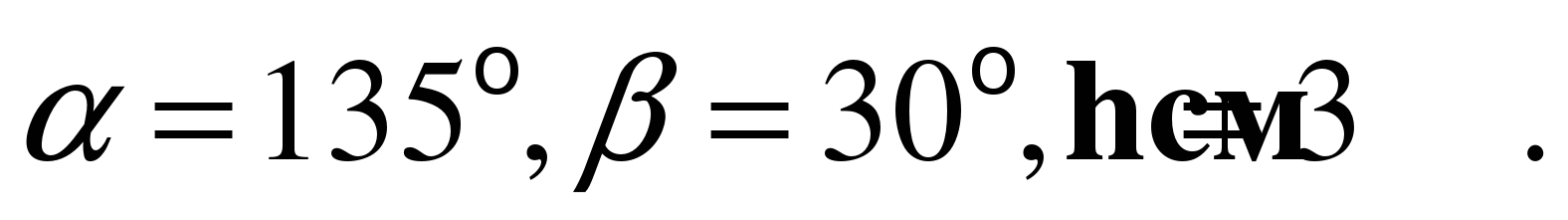
4. Хорда окружности равна а и стягивает дугу в 60о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Просмотр содержимого документа
«Контрольная работа № 2 Соотношения между сторонами и углами треугольника НН»
Просмотр содержимого документа
«Контрольная работа №1 Метод координат НН»
Г - 9 Контрольная работа № 1
Метод координат
Вариант 1
1.Найдите координаты и длину вектора  если
если  ,
, 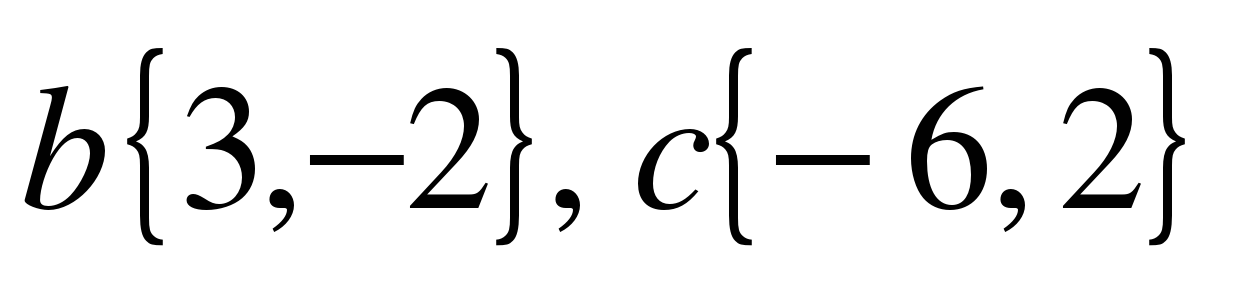 .
.
2. Даны координаты вершин треугольника ABC: A (-6; 1), B (2; 4), С (2; -2).
Докажите, что треугольник ABC равнобедренный, и найдите высоту треугольника, проведенную из вершины A.
3. Окружность задана уравнением 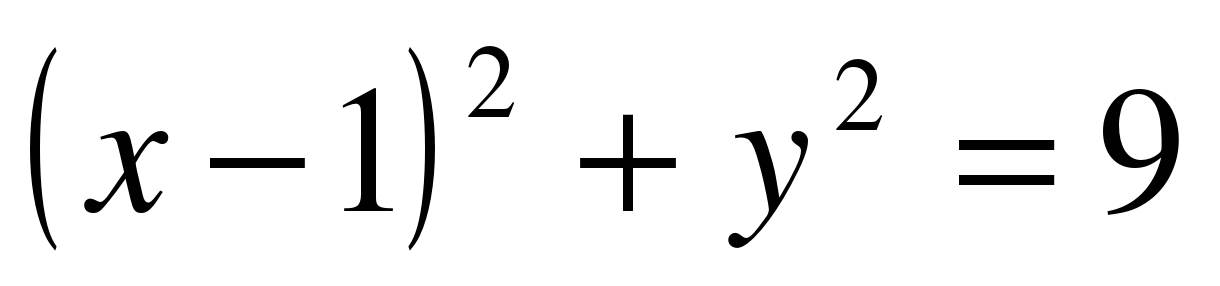 . Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат
. Напишите уравнение прямой, проходящей через её центр и параллельной оси ординат
.4. Напишите уравнение окружности с центром в точке А (- 1;4), проходящей через точку
В (3; - 1).
5. * Найдите координаты точки F, лежащей на оси абсцисс и равноудалённой от точек N и M, если N( - 2; 1 ) и M( 0; 3 ).
Контрольная работа № 1
Метод координат
Вариант 2
1.Найдите координаты и длину вектора  если
если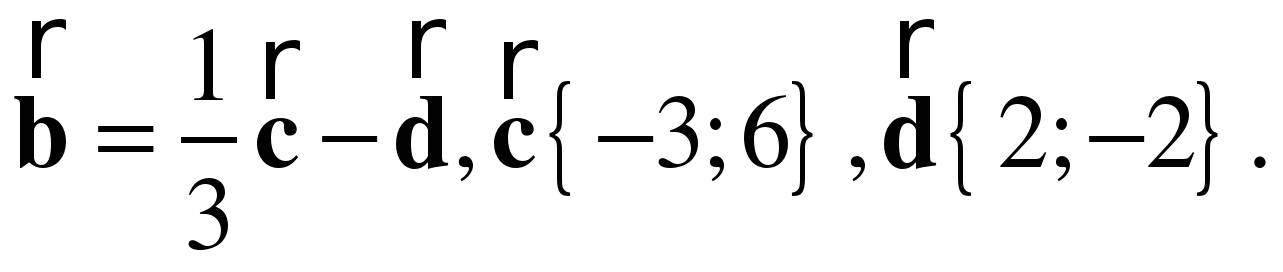
2. Даны координаты вершин четырехугольника ABC D: A (-6; 1), B (0; 5), С (6; -4),D (0; -8).
Докажите, что ABCD – прямоугольник, и найдите координаты точки пересечения его диагоналей.
3. Окружность задана уравнением  Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
Напишите уравнение прямой, проходящей через её центр и параллельной оси абсцисс.
4. Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку
D ( 5; 5 ).
5. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; - 3 ) и С( 2; 0 ).
Просмотр содержимого документа
«Контрольная работа №3 Длина окружности и площадь круга НН»
Просмотр содержимого документа
«Контрольная работа №4 Движения НН»















