Критические записки учителя,проводившего урок математике в 3 классе

Муниципальное общеобразовательное учреждение

средняя общеобразовательная школа с.Решетино.

Методическая разработка

Тема разработки: Критические записки учителя, проводившего

открытый урок по математике в 3 классе.

Форма проведения дела: (урок)

Адресат: (учителя начальных классов)

Автор, разработчик, составитель: Кармеева Альфия Назымовна,

учитель начальных классов

Кармеев Адгам Камилович

Физики и математики.

2019 г.

Аннотация

В данной методической разработке приводится анализ одного поурочного конспекта: недостатки и преимущества. На основе анализа составляются рекомендации для составления поурочного плана с учетом психологического анализа развития детей.

СОДЕРЖАНИЕ

Критические записки по этапам урока.

1.Общий обзор конспекта.

2.Актуализация знаний.

3. «Открытие» нового знания. Из истории дробей.

4. «Открытие» нового знания. Практическая работа с геометрическим материалом.

5.Методические рекомендации.

В этой работе мы проанализируем план урока, которую я провела перед учителями района. Конспект урока приводится в конце этой методической разработки (смотри методическую разработку.)

В целом конспект написан посредственно, но качество его можно несколько повысить: если в начале математического урока показать мультипликационный фильм «Апельсин», в котором «персонажи» делят апельсин на доли. (Тема урока «Доли».)

Таким образом, мы улучшили поурочный план добавлением технических средств обучения, которые с самого начала позволяют включить зрительную и другие виды памяти, а также мыслительную деятельность.

Рассмотрим некоторые модели развития памяти и мышления:

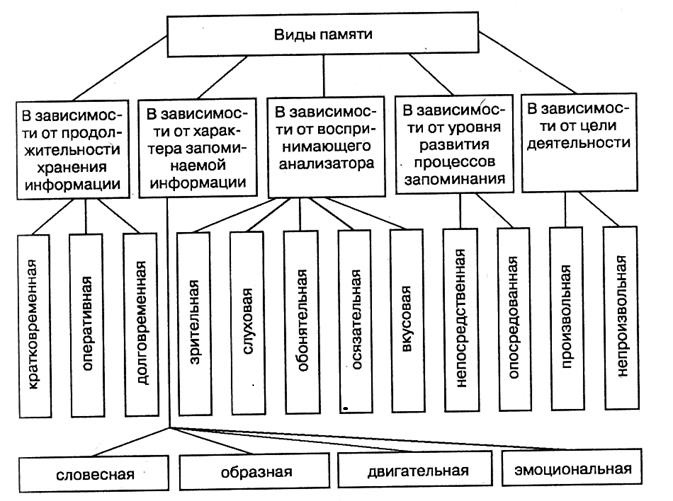
Посмотрели мультипликационный фильм, включаются в деятельности все виды памяти и все компоненты этой модели, хотя у каждого ученика уровень по компонентам разная. Ведь ученики делятся по усвоению знаний на слабых, средних, сильных.

Таким образом, при просмотре мультфильма оптимально работает мозг каждого ученика.

Не так эффективен презентация, но у каждой формы работы есть плюсы и минусы.

Учитель располагает уровнями памяти и мышления каждого ученика, с учетом всех своих данных он и составляет план урока. И конечно на уроке он импровизирует, всего предусмотреть невозможно. Подбирает оптимальные содержания, формы, средства, методы и целей обучения.

Рассмотрим другую модель. Хотя в фильме апельсин не пахнет и нельзя рукой дотянуться и вырвать апельсин, у ребенка включается обонятельная и вкусовая памяти. В данном случае математические задачи являются средством для развития разных видов памяти и наоборот.

Например, вот задача на запоминание цифр, придуманная психологами, а в математике все задачи на развитие памяти, просто учитель должен видеть это.

развитие памяти на цифры, буквы, слова Покажите ребенку цифровой ряд, написанный на карточке, и попросите его повторить в той же последовательности эти цифры, затем увеличивайте этот ряд на одну цифру: 6 2

2 8 3

3 7 1 4

6 3 9 1 5

8 1 4 9 2 6

7 4 1 8 3 9 2

Отметьте, какое максимальное количество цифр может повторить ребенок.

Далее предложите ребенку выполнить то же самое задание, но только зачитывая цифры без показа. (В первом случае вы определяли зрительную память, а во втором слуховую) В третьей серии попробуйте научить ребенка одному из способов расширения способности к запоминанию. Начните с того цифрового ряда, который ребенок уже не смог повторить. Для того чтобы легче запомнить каждую цифру, научите ребенка отыскивать какую-нибудь аналогию с соответствующим числом. Например, какое то число совпадает с возрастом ребенка, какое - то - с номером квартиры и т.д. Теперь ему будет легче воспроизвести этот цифровой ряд. Продолжите подобную тренировку, но пусть ребенок сам пытается найти какие - либо аналогии для того чтобы затем воспроизвести цифровой ряд.

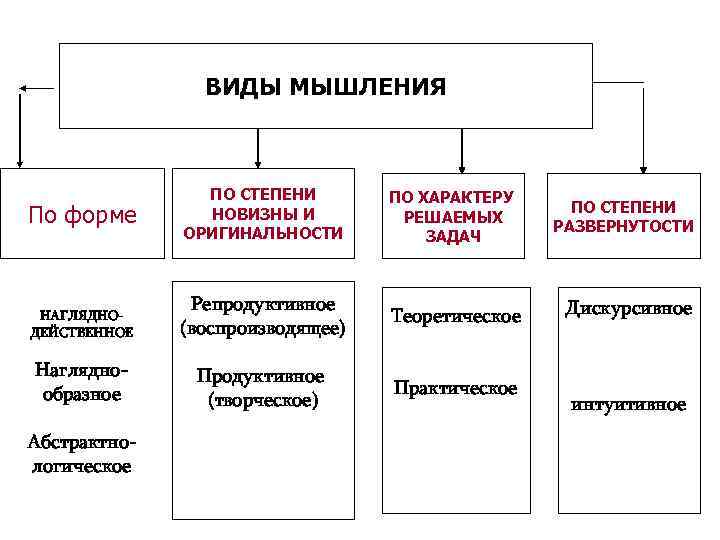
В математике каждая задача для развития памяти и мышления. Учитель должен видеть это и применять, что поможет ему для дальнейшей преподавательской работе.

Используя эти модели легко заметить, какие компоненты задействованы.

Теперь рассмотрим сам конспект урока и решим задачу: как улучшить содержание конспекта.

Рассмотрим эту часть в подлиннике:

Не все ученики участвовали в решении первой части задачи. И даже после того, как сильные ученики выполнили, некоторые смотрели недоуменно. Но если часть учеников не поняли, необходимо учителю что-то предпринять. В данном случае учитель может организовать на этом этапе групповую работу. В группе есть сильные, слабые, средние. Для групповой работы предоставляются аналогичные новые задания.

Теперь рассмотрим 5 часть конспекта: «Открытие» нового знания. Из истории дробей.

Этот этап урока несложный, но и в нем могут быть препятствия в усвоении знаний детьми. Каждый вопрос - это задача, требует определенного уровня мышления.

Учитель подводит к «главному» наводящими вопросами:

-Смогу ли я одно яблоко разделить между двумя людьми?

-Как мне это сделать, ведь яблоко одно?

-Как это записать?

В объяснении нового материала конспект составлен с учетом «Зоны ближайшего развития»

Составитель конспекта сделал все правильно, потому что ученики в основном поняли объясняемую тему.

Далее разбираем часть «Открытие нового знания. Практическая работа с геометрическим материалом.

Итак, каждый вопрос - это задача. В сложных вопросах некоторые ученики затрудняются, причина заключена в возможностях учащихся в «операциональной мыслительной деятельности».

« ОПЕРАЦИОНАЛЬНОЕ МЫШЛЕНИЕ»

Общее название Пиаже для когнитивных принципов, участвующих в конкретных операциях и формальных операциях. Обратите внимание, что сторонники Пиаже ограничивают использование термина операциональный этими двумя когнитивными стадиями, на которых дети демонстрируют модели поведения, которые обнаруживают мышление, управляемое логической системой. См. и ср. с предоперациональным мышлением. Также называется иногда операторным мышлением; см. статью операциональный о замечаниях по поводу употреблении Рассмотрим некоторые модели «Операциональной мыслительной деятельности».

В силу следующих причин, которые описываются в этой модели, дети не могут решить некоторые задачи. Решить эту проблему можно расчленив сложные задачи на простые. Этот ход необходим для данной категорий учащихся. И наоборот, можно усложнить более простые задачи в сложные.

Структурирование материала. Материал воспринимается и за­поминается лучше, если он преподносится в структурированном виде. Для этого необходимо выделять части параграфа или эле­менты материала, показывать и фиксировать связи между ними. Этот процесс можно облегчить выделением ключевых, или опор­ных слов, которые отражают сущность той или иной части мате­риала (можно использовать схемы, образы, ассоциации и т. д.). Особо следует отметить необходимость выделения главного в информации. Педагог должен стремиться выделить наиболее су­щественное всеми средствами: голосом, словами, рисунками, до­полнительными упражнениями и т. д. Или другое мнение на этот счет.

Гештальтпсихологи на основе экспериментальных данных при­шли к выводу, что лучше запоминается материал, удовлетворяю­щий критериям «хорошей формы» в отношении упорядоченности, простоты и симметричности. Поэтому в процессе запоминания, там, где это возможно, целесообразно объединение материала в структуру посредством его слияния и последующего объединения путем ритмизации, симметричного расположения и т. д.

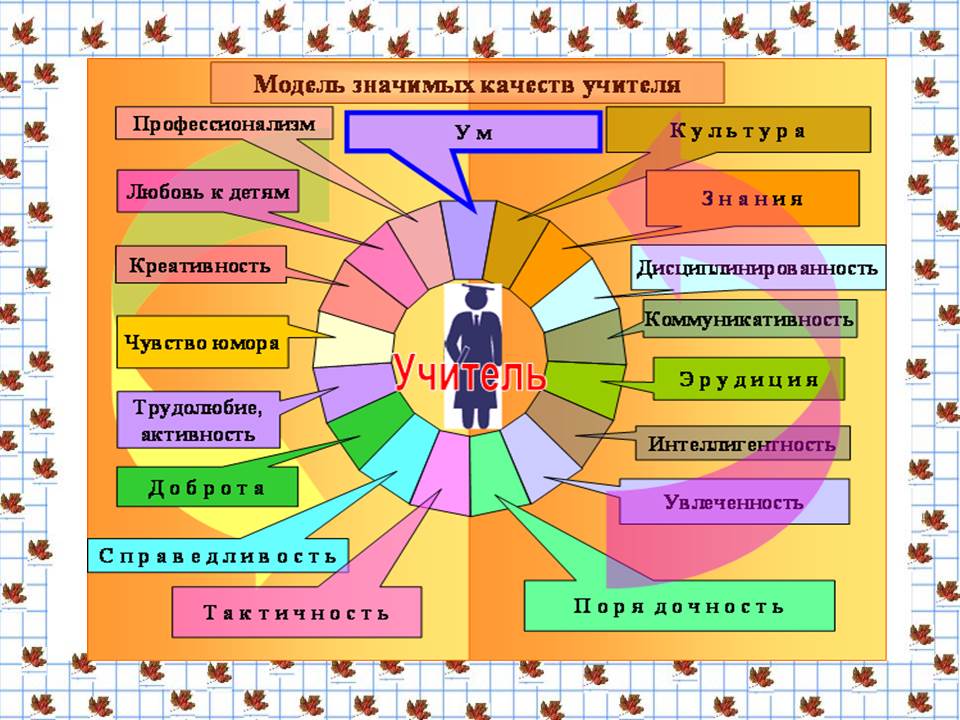
В итоге, чтобы решить возникшие проблемы при проведении урока учитель должен обладать определенными качествами.

Методические рекомендации:

1.Среди целей поурочного плана должна быть главная цель, на котором учитель более концентрирует свое внимание.

2.Содержание, методы, формы, средства, цели обучения должны рассматриваться как единое целое.

3.Преодолеть трудности в обучении нужно расчленив трудные задачи на простые и наоборот.

4.Чтобы оптимально решить проблемы в обучении необходимо учителю саморазвитие.

5.Составление поурочного плана необходимо сочетать с психологическим анализом развития детей.

Литература:

1. Выготский Л.С. Мышление и речь. — Лабиринт, 2012. — С. 25-33.

2. Выготский Л.С. Мышление и речь. — Лабиринт, 2012. — С. 44—47.

3. Пиаже Ж. Речь и мышление ребенка. — Педагогика - Пресс, 1999. — С. 74.

4. Пиаже Ж. Речь и мышление ребенка. — Педагогика - Пресс, 1999. — С. 173.

5. Фридман Л. М., Турецкий Е. Н. Как научиться решать задачи. — М, 1989

6. Фридман Л. М. Логико-психологический анализ школьных учебных задач. — М.: Педагогика, 1977. — 208с.