

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Кружок "Математический серпантин"
Планирование кружка "Математический серпантин"в помощь учителям во внеурочной деятельности
Просмотр содержимого документа
«Кружок "Математический серпантин"»
Государственное бюджетное общеобразовательное
учреждение Республики Крым
«Крымская гимназия-интернат для одаренных детей»
| РАССМОТРЕНО на заседании МО учителей естественно-математического цикла Протокол от «____» _____ 2019 №____ Руководитель МО ___________ Е.Н. Вьюн
| СОГЛАСОВАНО заместитель директора по УМР __________В.А.Марченко
| УТВЕРЖДЕНО Директор ______________Ю.А. Тулаев Приказ от «____» _____ 2019 №____
|
РАБОЧАЯ ПРОГРАММА
По дополнительному образованию
кружка
«Математический серпантин»
6 – А, Б, В классы
(2часа в неделю – 68часов в году)
Разработчик программы:
Эбушеитова Эльвира Меметовна,
учитель математики высшей категории
г. Симферополь
2019г.
Давно замечено, что таланты являются
всюду и всегда, где и когда существуют
условия, благоприятные для их развития.
(Г. В. Плеханов)
Пояснительная записка
Внеурочная деятельность регламентируется следующими документами:
-письмом Министерства образования и науки российской Федерации от12.05.2011 №03-296 «Об организации внеурочной деятельности при введении федерального государственного образовательного стандарта общего образования»;
-письмом Министерства образования, науки и молодёжи Республики Крым от 04. 12. 2014 №01-14/2014.
Программа кружка «Математический серпантин» относится к научно-познавательному направлению.
Содержание программы соответствует познавательным возможностям школьников и предоставляет им возможность работать на уровне повышенных требований,
развивая учебную мотивацию.
Актуальность программы определена тем, что обучающиеся 6-го класса должны иметь мотивацию к обучению математики, стремиться развивать свои интеллектуальные возможности.
Одной из главных задач является привитие устойчивого интереса к предмету, развитие математических способностей младших школьников, подготовка к обучению в старших классах.
Основное внимание на занятиях по данной программе уделяется развитию навыков вариативного мышления, простейшим методам исследования. Особое внимание уделяется развитию умения мыслить логически, стараться преодолеть сформированный конформизм, умению не только найти решение, но и оптимизировать его, познакомиться с тем, что не все поставленные проблемы имеют решение, уметь доказывать этот факт.
Решение математических задач, связанных с логическим мышлением закрепит интерес детей к познавательной деятельности, будет способствовать развитию мыслительных операций и общему интеллектуальному развитию.
Не менее важным фактором реализации данной программы является и стремление развить у учащихся умений самостоятельно работать, думать, решать творческие задачи, а также совершенствовать навыки аргументации собственной позиции по определенному вопросу.
Внеурочные занятия должны содействовать развитию у детей математического образа мышления. Творческие работы, проектная деятельность и другие технологии, используемые в системе работы кружка, должны быть основаны на любознательности детей, которую следует поддерживать и направлять. Данная практика поможет ему успешно овладеть не только общеучебными умениями и навыками, но и осваивать более сложный уровень знаний по предмету, достойно выступать на олимпиадах и участвовать в различных конкурсах.
Цели и задачи программы:
Цели:
развитие логического мышления;
развитие математического образа мышления;
развивитие критичности мышления, интуиции;
формирование навыков исследовательской деятельности;
обучение принципам сравнения и поиску закономерностей;
приобретение научных знаний по предмету;
развитие познавательных способностей учащихся, направленных на формирование универсальных учебных действий на основе предметно ориентированного тренинга;
формирование учебно-интеллектуальных, информационно-коммуникативных, исследовательских умений;
развитие аналитико-синтетических способностей;
формирование устойчивого интереса к предмету;
совершенствование навыков самостоятельной работы;
воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;
развитие представлений о математике как о форме описания и методе познания действительности, создание условий для приобретения первоначального опыта моделирования;
углубление практических знаний, умений и навыков учащихся, являющихся значимыми для различных сфер человеческой деятельности.
Задачи:
расширить знания обучающихся о методах решения нестандартных задач;
выработать умения решать задачи разных типов;
выработать умения выдвигать гипотезу и проводить исследования, тем самым доказывая или опровергая её;
выработать умения анализировать, проводить сравнения, рассматривая различные значения неизвестных;
выработать умения абстрагироваться, умения перевести задачу с естественного языка на математический;
мотивировать деятельность обучающихся, пробудить интерес к участию в различных конкурсах и олимпиадах;
мотивировать на продолжение изучения данного предмета;
создать базу для успешного изучения других предметов естественнонаучного цикла.
Сроки реализации программы
Программа рассчитана на один год обучения, 68 учебных часов. Занятия проводятся 2 часа в неделю.
Формы занятий
На занятиях предусматриваются следующие формы организации учебной деятельности:
- индивидуальная (воспитаннику дается самостоятельное задание с учетом его возможностей);
- фронтальная (работа в коллективе при объяснении нового материала или отработке определенной темы);
- групповая (разделение на мини группы для выполнения определенной работы);
- коллективная (выполнение работы для подготовки к олимпиадам, конкурсам).
Основные виды деятельности учащихся
1.Решение занимательных задач.
2.Оформление математических газет, сообщений, презентаций.
3.Участие:
- во Всероссийской математической олимпиаде;
- в Международной игре- конкурсе «Кенгуру»,;
-в дистанционной олимпиаде «Фоксфорд»;
4.Знакомство с научно-популярной литературой, связанной с математикой;
5.Проектная и исследовательская деятельность ;
6.Самостоятельная работа;
7.Работа в парах, в группах;
8.Творческие работы.
Результаты освоения программы
Личностные:
1) ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;
2) формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими в образовательной, учебно-исследовательской, творческой и других видах деятельности;
3) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
4) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
5) креативность мышления, инициатива, находчивость, активность при решении арифметических задач;
6) умение контролировать процесс и результат учебной математической деятельности;
7) формирование способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
Метапредметные:
1) способность самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
2) умение осуществлять контроль по образцу и вносить необходимые коррективы;
3) способность адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
4) умение устанавливать причинно-следственные связи; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы;
5) умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
6) развитие способности организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределять функции и роли участников, взаимодействовать и находить общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
7) развития способности видеть математическую задачу в других дисциплинах, в окружающей жизни;
8) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
9) умения понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
10) умение выдвигать гипотезы при решении учебных задач и понимание необходимости их проверки;
11) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем.
Предметные:
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), развития способности обосновывать суждения, проводить классификацию;
умение пользоваться изученными математическими формулами;
умение решать задачи с помощью перебора всех возможных вариантов;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Содержание программы
Вводная беседа «Зачем решать нестандартные задачи?» (1ч)
Занимательное в математике(9часов)
Магические фигуры, ребусы, головоломки, кроссворды. Математические фокусы и софизмы. Занимательный счет.
Логические задачи (31 часов)
Задачи на делимость чисел. Задачи на принцип Дирихле. Комбинаторные задачи. Задачи решаемые с помощью графов.Высказывания. Истинные и ложные высказывания. Отрицание высказываний. Составление отрицаний высказываний. Обратные высказывания.Доказательство от противного. Задачи, решаемые с конца,круги Эйлера
Основная цель: развитие умения логически сопоставлять условие задачи с конечной целью. Анализ основных методов решения. Получить навыки отделять аранжировку задачи от истинной фабулы объектов рассматриваемой проблемы. Приобрести первичные навыки творчества.
Взвешивания и переливания (11 часов)
Алгоритм, чашечные весы, весы со стрелкой, построение оптимального алгоритма, , переливания.
Основная цель: выработать навык построения оптимального алгоритма. Обучающиеся должны привыкнуть к мысли, что часто существует много правильных решений одной и той же задачи, познакомиться с примерами разумной записи решений задач на переливания и взвешивания, приобрести опыт мыслительного, образного и предметно-манипулятивного конструирования.
Текстовые задачи на дроби и проценты (16 часов)
Нахождение части и процента от числа. Формула сложных процентов. Банковские расчёты.
Основная цель: показать практическое применение задач в реальной жизни. Научить решать задачи повышенной сложности на нахождение процентов и дробей от числа. Закрепить навыки находить часть и процент от числа, навыки составления уравнений по условию задач, познакомить с понятием «банковские проценты».Задачи на составление уравнений,систем уравнений,совместную работу.
Используемая литература
И.В Шарыгин, А.В. Шевкин. «Задачи на смекалку 5-6 кл.».-М.: «Просвещение»,2015г.
А.В.Шевкин « Математика-это интересно».- М.: «Илекса», 2015г.
Е.Г.Козлова. Сказки и подсказки. М.: МЦНМО,2006.
И.В.Раскина. Логика для всех: от пиратов до мудрецов. М.: МЦНМО,2016.
И.В.Раскина, Д.Э.Шноль. Логические задачи. М.: МЦНМО,2014.
К.А. Кноп. Взвешивания и алгоритмы: от головоломок к задачам. М.: МЦНМО,2014.
А.В.Спивак. Тысяча и одна задача по математике. - М.: «Просвещение», 2010.
П.В.Чулков. Арифметические задачи.М.: МЦНМО,2009.
8. И.Я. Депман, Н.Я. Виленкин. «За страницами учебника математики: Пособие для учащихся 5 – 6 классов сред школ. – М.: «Просвещение», 1989 г.
9. «Все задачи "Кенгуру"», С-П.,.
10. Л.М.Лихтарников. «Занимательные задачи по математике», М.,1996г.
11. Е.В.Галкин. «Нестандартные задачи по математике», М., 1996г.
12. А.Я.Кононов. «Математическая мозаика», М., 2004 г.
13. Б.П.Гейдман. «Подготовка к математической олимпиаде», М., 2007 г.
14. Т.Д.Гаврилова. «Занимательная математика», изд. Учитель, 2005 г.
15. Е.В.Галкин. «Нестандартные задачи по математике, 5-11 классы», М., 1969 г.16. «Ума палата» - игры, головоломки, загадки, лабиринты. М., 1996г.
16. Е.Г.Козлова. «Сказки и подсказки», М., 1995г.
17. И.В.Ященко «Приглашение на математический праздник». М., МЦНПО, 2005г.
18. А.С.Чесноков, С.И.Шварцбурд, В.Д.Головина, И.И.Крючкова, Л.А.Литвачук. «Внеклассная работа по математике в 4 – 5 классах». / под ред. С.И.Шварцбурда. М.: «Провсещение», 1974
19. А. Я.Котов. «Вечера занимательной арифметики»
20. Ф.Ф.Нагибин. «Математическая шкатулка». М.: УЧПЕДГИЗ, 1961 г.
21. Е.И.Игнатьев. Математическая смекалка. Занимательные задачи, игры, фокусы, парадоксы. – М., Омега, 1994 г.
Интернет ресурсы:
Удивительный мир математики. http://www.math.ru.
Московский центр непрерывного математического образования. http://www.conte.ru.
Математический калейдоскоп, случаи, фокусы, парадоксы. http:// mathc.chat.ru/
Всероссийские дистанционные эвристические олимпиады. http://eidos.ru/olymp/
Международный конкурс «Кенгуру» [email protected].
Всероссийская дистанционная конкурс-игра «КИО-2011» http://www.ipo.spb.ru/kio/.
Открытая российская интернет олимпиада по математике. metaschool.ru.
| № п/п | Тема занятия | Количество часов | Дата проведения по плану | Дата проведения по факту | |
| 1 | Зачем решать нестандартные задачи? | 1 | 04.09 |
| |
|
|
|
|
|
| |
|
| Занимательное в математике(9часов) |
| |||
| 2-3 | Магические фигуры | 2 | 04.09 11.09, |
| |
| 4-5 | Ребусы, головоломки, кроссворды | 2 | 11.09,18.09 |
| |
| 6-7 | Математические фокусы и софизмы | 2 | 18.09, 25.09 |
| |
| 8-9 | Занимательный счет | 2 | 25.09, 02.10 |
| |
|
|
|
|
|
| |
|
| Логические задачи (31 часов) |
| |||
| 10-11 | Логические задачи решаемые с помощью таблиц | 2 | 02.10, 09.10 |
| |
| 12-13 | Задачи на делимость чисел | 2 | 09.10, 16.10 |
| |
| 14-15 | Задачи на принцип Дирихле | 2 | 16.10, 23.10 |
| |
| 16-19 | Комбинаторные задачи | 4 | 23.10, 30.10, 30.10, 06.11 |
| |
| 20-22 | Задачи решаемые с помощью графов | 3 | 06.11, 13.11, 13.11 |
| |
| 23-24 | Высказывания и их отрицания. | 2 | 20.11, 20.11 |
| |
| 25-26 | «Все», «некоторые» и отрицание. | 2 | 27.11, 27.11 |
| |
| 27-28 | Примеры и контрпримеры. | 2 | 04.12, 04.12 |
| |
| 29-30 | Высказывания с «и», «или». | 2 | 11.12, 11.12 |
| |
| 31-32 | Следствие и обратные высказывания. | 2 | 18.12, 18.12 |
| |
| 33-34 | Доказательство от противного. | 2 | 25.12, 25.12 |
| |
| 35-36 | Равносильность. | 2 | 15.01, 15.01 |
| |
| 37-39 | Круги Эйлера | 3 | 22.01, 22.01, 29.01 |
| |
| 40-41 | Мини олимпиада. | 2 | 29.01, 05.02 |
| |
| Взвешивания и переливания (11 часов) | |||||
| 42 | Что такое алгоритм? | 1 | 05.02 |
| |
| 43-44 | Задачи с монетами. | 2 | 12.02, 12.02 |
| |
| 45-46 | В поисках случая. | 2 | 19.02, 19.02 |
| |
| 47-48 | Весы со стрелкой. | 2 | 26.02, 26.02 |
| |
| 49-50 | Задачи на взвешивание | 2 | 04.03, 04.03 |
| |
| 51-52 | Задачи на переливания | 2 | 11.03, 11.03 |
| |
| Текстовые задачи на дроби , проценты, уравнения(16часов) | |||||
| 53-56 | Задачи на проценты | 4 | 25.03, 25.03, 01.04, 01.04 |
| |
| 57-58 | Сложные проценты. | 2 | 08.04, 08.04 |
| |
| 59-60 | Дроби и двойной остаток. | 2 | 15.04, 15.04 |
| |
| 61 | Банковские расчёты. | 1 | 22.04 |
| |
| 62-63 | Задачи решаемые с помощью уравнений | 2 | 22.04, 29.04 |
| |
| 64-65 | Задачи на совместную работу | 2 | 29.04, 13.05 |
| |
| 66-67 | Задачи на системы уравнений | 2 | 13.05, 20.05 |
| |
| 68 | Игра «МАТБОЙ» | 1 | 20.05 |
| |
|
|
|
|
|
| |
ПРИЛОЖЕНИЕ
Логические задачи – это хороший способ развития умственных способностей для школьников всех возрастов.
--------------------------------------------------------------------------------------
Круги Эйлера – задачи на пересечение или объединение множеств
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче. "Обитаемый остров" и "Стиляги"
Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение
Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».
11 – 6 = 5 – человек, которые смотрели только «Стиляги».
Получаем:

Ответ. 5 человек смотрели только «Стиляги».
Любимые мультфильмы
Среди школьников шестого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?
Решение
В этой задаче 3 множества, из условий задачи видно, что все они пересекаются между собой. Получаем такой чертеж:
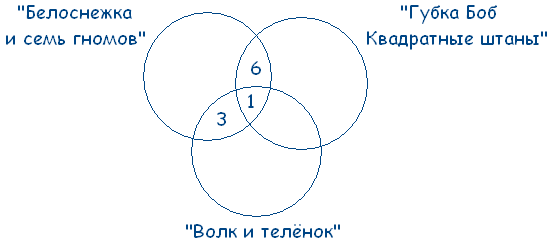
Учитывая условие, что среди ребят, которые назвали мультфильм «Волк и теленок» пятеро выбрали сразу два мультфильма, получаем:

21 – 3 – 6 – 1 = 11 – ребят выбрали только «Белоснежку и семь гномов».
13 – 3 – 1 – 2 = 7 – ребят смотрят только «Волк и теленок».
Получаем:

38 – (11 + 3 + 1 + 6 + 2 + 7) = 8 – человек смотрят только «Губка Боб Квадратные Штаны».
Делаем вывод, что «Губка Боб Квадратные Штаны» выбрали 8 + 2 + 1 + 6 = 17 человек.
Ответ. 17 человек выбрали мультфильм «Губка Боб Квадратные Штаны».
------------------------------------------
«Мир музыки»
В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры?
Решение
Изобразим эти множества на кругах Эйлера.

Теперь посчитаем: Всего внутри большого круга 35 покупателей, внутри двух меньших 35–10=25 покупателей. По условию задачи 20 покупателей купили новый диск певицы Максим, следовательно, 25 – 20 = 5 покупателей купили только диск Земфиры. А в задаче сказано, что 11 покупателей купили диск Земфиры, значит 11 – 5 = 6 покупателей купили диски и Максим, и Земфиры:

Ответ: 6 покупателей купили диски и Максим, и Земфиры.
---------------------------------------------------------------------------------------------
Задачи типа "Кто есть кто?"
Задачи типа «Кто есть кто?» - это самые что ни на есть логические задачи. Льюис Кэрролл очень любил создавать такие, и непрерывно потчевал ими своих студентов, так как был профессором математики. Но вы можете сколько вашей душе угодно решать логические задачи, развивая свою память и интеллект.
Смысл задач под кодовым названием «Кто есть кто?» довольно прост. Вам даны отношения между предметами и следуя по цепочке этих отношений, вы приходите к правильному результату.
Существует несколько методов решения задач типа «Кто есть кто?». Один из методов решения таких задач – метод графов. Второй способ, которым решаются такие задачи – табличный способ.
Любители музыки
В клубе «Отдых» познакомились 3 любителя клубной музыки видов техно, хаус, рейв. Один говорит: «Вы какую музыку больше любите? Я техно люблю!». Другой ответил, что любит хаус, а третий сказал, что не любит ни техно, ни хаус, но зато обожает рейв. Интересно то, что все они были в банданах и рубашках черного, белого и желтого цветов, но цвет банданы и рубашки совпадал только у любителя техно. А у любителя хаус ни рубашка, ни бандана не были белыми. А любитель рейв был в желтой рубашке. Определите цвет рубашек и бандан каждого из любителей клубной музыки.
Решение Заметим, что по условию задачи цвет банданы и рубашки совпадал только у любителя техно. А так как у любителя хаус ни рубашка ни бандана не были белыми и любитель рейв был в желтой рубашке, то делаем вывод, что любитель техно может быть в рубашке и бандане только белого цвета.
Получаем граф:

Решение сводится к нахождению трех сплошных треугольников с вершинами в разных множествах. Значит у любителя хаус желтая бандана и черная рубашка (т.к. цвет совпадал только у любителя техно по усл.), а у любителя рейв черная бандана.

Ответ. У любителя техно рубашка и бандана белого цвета; у любителя хаус черная рубашка и желтая бандана; у любителя рейв желтая рубашка и черная бандана.
Футбол
Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Марк. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно:
а) Зенит не тренируется у Марка и Антонио.
б) Милан обещал никогда не брать Марка главным тренером.
Решение
Исходя из условий задачи, получаем следующий граф.

Сразу можем сделать вывод, что российская команда «Зенит» тренируется у испанца Родриго. Чертеж примет вид:

Теперь получили, что итальянская команда «Милан» тренируется у русского Николая. Внесем и эти изменения в чертеж, получим:

Приходим к выводу, что английская команда «Челси» тренируется у итальянца Антонио и испанская команда «Реал» тренируется у англичанина Марка.
Ответ. Российская команда «Зенит» тренируется у испанца Родриго; итальянская команда «Милан» тренируется у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда «Реал» тренируется у англичанина Марка.
Три поросёнка
Жили-были на свете три поросенка, три брата: Ниф-Ниф, Наф-Наф, Нуф-Нуф. Построили они три домика: соломенный, деревянный и кирпичный. Все три брата выращивали возле своих домиков цветы: розы, ромашки и тюльпаны. Известно, что Ниф-Ниф живет не в соломенном домике, а Наф-Наф – не в деревянном; возле соломенного домика растут не розы, а тот, у кого деревянный домик, выращивает ромашки. У Наф-Наф аллергия на тюльпаны, поэтому он не выращивает их. Узнайте, кто в каком домике живет и какие цветы выращивает.
Решение
Из условий задачи получаем граф:

Можно сделать вывод, что возле кирпичного домика растут розы, а возле соломенного – тюльпаны. А так как Наф-Наф живет не в деревянном домике, то он и не выращивает ромашки. А так как на тюльпаны у него аллергия, то он может выращивать только розы. Внесем эти данные в чертеж и получим:

Теперь стало ясно и то, что Ниф-Ниф живет в деревянном домике и выращивает ромашки. Методом исключения получаем, что Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Ответ. Наф-Наф живет в кирпичном домике и выращивает розы; Ниф-Ниф живет в деревянном домике и выращивает ромашки; Нуф-Нуф живет в соломенном домике и выращивает тюльпаны.
Соревнование по фехтованию
Атос, Портос и Арамис в соревновании по фехтованию заняли три первых места. Какое место занял каждый из них, если Портос занял не второе и не третье место, а Арамис – не третье?
Решение
Учитывая условия задачи, сразу делаем вывод, что Портос занял первое место. Значит, Арамис занял второе место, и Атос – третье место. Решение задачи показано на чертеже:

Ответ. Арамис – второе место; Атос – третье место; Портос – первое место.
Компьютерные игры
В компьютерном классе на уроке информатики, во время отсутствия учителя, пять ребят – Максим, Настя, Саша, Рома, Сережа – отвлеклись от нужной работы и стали играть в такие игры: пасьянс «Паук», гонки, сапер, «Марио», тетрис. Каждый из них играл только в одну игру.
• Саша думал, что в «Марио» играет Настя.
• Настя предполагала, что Рома играет в тетрис, а Максим – в гонки.
• Рома считал, что Сережа играет в гонки, а Саша – в сапера.
• Максим думал, что Настя раскладывает пасьянс «Паук», а в «Марио» играет Рома.
В результате оказалось, что все они ошиблись в своих предположениях. Кто и во что играл?
Решение
Таблица с известными запретами (исходя из условия задачи):
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра | |||||
| Пасьянс «Паук» | - | - |
|
|
|
| Гонки | - | - |
| - | - |
| Сапер |
|
| - | - |
|
| «Марио» | - | - | - | - |
|
| тетрис |
| - |
| - |
|
Известно, что каждый из игравших играл только в одну, значит, в каждой строке и каждом столбце таблицы может стоять только один «+».
Из условий задачи следует, что Саша не играл в «Марио»; Настя не играла ни в тетрис, ни в гонки; Рома – ни в гонки, ни в сапера; Максим – ни в пасьянс «Паук», ни в Марио.
Так как все предположения ошибочны, то Настя не играет в «Марио», Рома – в тетрис, Максим – в гонки, Сережа – в гонки, Саша – в сапера, Настя – в пасьянс «Паук», Рома – в «Марио».
Используем правило, что если в строке (или столбце) все места, кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+». В строчке «гонки» можно поставить «+» напротив имени Саша, а в строчке «Марио» напротив имени Сережа. Получаем:
| Имя | Максим | Настя | Саша | Рома | Сережа |
| Игра | |||||
| Пасьянс «Паук» | - | - | - |
| - |
| Гонки | - | - | + | - | - |
| Сапер |
|
| - | - | - |
| «Марио» | - | - | - | - | + |
| тетрис |
| - | - | - | - |
Теперь становится ясно, что в пасьянс «Паук» играл Рома, в сапера – Настя, а в тетрис – Максим. Задача решена.
Ответ. Сережа играл в «Марио»; Рома – в пасьянс «Паук»; Саша – в гонки; Настя – в сапера; Максим – в тетрис.
Студенты
Дина, Соня, Коля, Рома и Миша учатся в институте. Их фамилии – Бойченко, Карпенко, Лысенко, Савченко и Шевченко.
Рома никогда не видел своей мамы.
Родители Дины никогда не встречались с родителями Коли.
Студенты Шевченко и Бойченко играют в одной баскетбольной команде.
Услышав, что родители Карпенко собираются поехать в город, мать Шевченко пришла к матери Карпенко и попросила, чтобы та отпустила своего сына к ним на вечер, но оказалось, что отец Коли уже договорился с родителями Карпенко и пригласил их сына к Коле.
Отец и мать Лысенко – хорошие друзья родителей Бойченко. Все четверо очень довольны, что их дети собираются пожениться.
Установите имя и фамилию каждого из молодых людей и девушек.
Решение
Учитывая то, что у Ромы не было мамы, можно сделать вывод, что Рома – не Карпенко, не Шевченко, не Лысенко и не Бойченко. Следовательно, он Савченко. Также, из условия задачи видно, что Карпенко парень, следовательно, он - не Дина, не Соня, и к тому же – не Коля («отец Коли уже договорился с родителями Карпенко»). Следовательно, Карпенко зовут Миша. Отметим это в таблице:
| Имя | Дина | Соня | Коля | Рома | Миша |
| Фамилия | |||||
| Шевченко |
|
|
| - | - |
| Савченко | - | - | - | + | - |
| Бойченко |
|
|
| - | - |
| Карпенко | - | - | - | - | + |
| Лысенко |
|
|
| - | - |
Как известно, в одной баскетбольной команде играют либо одни юноши, либо одни девушки. Пара «Шевченко + Бойченко» мужской быть не может, так как в качестве возможных претендентов на эти две фамилии у нас остались две девушки и один юноша. Следовательно, Шевченко и Бойченко – девушки. Получаем:
| Имя | Дина | Соня | Коля | Рома | Миша |
| Фамилия | |||||
| Шевченко |
|
| - | - | - |
| Савченко | - | - | - | + | - |
| Бойченко |
|
| - | - | - |
| Карпенко | - | - | - | - | + |
| Лысенко |
|
|
| - | - |
Значит, фамилия Коли – Лысенко. Это легко установить, взглянув на таблицу. Имеем:
| Имя | Дина | Соня | Коля | Рома | Миша |
| Фамилия | |||||
| Шевченко |
|
| - | - | - |
| Савченко | - | - | - | + | - |
| Бойченко |
|
| - | - | - |
| Карпенко | - | - | - | - | + |
| Лысенко | - | - | + | - | - |
Остается выяснить имя и фамилию каждой из девушек. Сопоставим два факта: «Родители дины никогда не встречались с родителями Коли (мы уже знаем, что его фамилия – Лысенко)» и «Родители Лысенко дружат с родителями Бойченко». Ясно, что Дина - не Бойченко. Следовательно, ее фамилия Шевченко, а фамилия Сони – Бойченко.
Ответ. Миша Карпенко; Рома Савченко; Коля Лысенко; Соня Бойченко; Дина Шевченко.
Мушкетёры
Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее:
• Атос и Арамис наблюдали на балу за их другом – прекрасным танцором.
• Портос и лучший стрелок вчера с восхищением следили за боем рукопашника.
• Стрелок хочет пригласить в гости Атоса.
• Портос был очень большой комплекции, поэтому танцы были не его стихией.
Кто чем занимается?
Решение
Таблица с известными запретами:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя | ||||
| Атос |
|
| - | - |
| Портос |
| - | - | - |
| Арамис |
|
| - |
|
| Д’Артаньян |
|
|
|
|
Известно, что каждый из четырех мушкетеров был лучшим только в одном деле. Следовательно, в каждой строчке и каждом столбце может стоять только один «+». Взглянув на таблицу, сразу можно сказать, что танцор – Д’Артаньян, шпажист – Портос. Вносим эти данные в таблицу. Получаем:
| Занятие | шпажист | рукопашник | танцор | стрелок |
| Имя | ||||
| Атос | - |
| - | - |
| Портос | + | - | - | - |
| Арамис | - |
| - |
|
| Д’Артаньян | - | - | + | - |
Теперь можно сделать вывод, что стрелок – это Арамис, рукопашник – Атос.
Ответ. Арамис – стрелок; Д’Артаньян – танцор; Портос – шпажист; Атос – рукопашник.
![]()
"Пепси", "Кока-Кола", квас и "Спрайт"
В бутылке, стакане, кувшине и банке находятся «Пепси», «Кока-кола», квас и «Спрайт». Известно, что «Спрайт» и «Пепси» не в бутылке, сосуд с «Кока-колой» находится между кувшином и сосудом с квасом, в банке – не «Кока-кола» и не «Спрайт». Стакан находится около банки и сосуда с «Пепси». Как распределены эти жидкости по сосудам?
Решение
Из условий задачи получаем таблицу с запретами:
| Сосуд | Бутылка | Стакан | Кувшин | Банка |
| Жидкость | ||||
| «Пепси» | - | - |
| - |
| «Кока-кола» |
|
| - | - |
| Квас |
|
|
|
|
| «Спрайт» | - |
|
| - |
Так как каждая жидкость находится только в одном сосуде, то в в каждой строчке и каждом столбце может стоять только один «+». Вглянув на таблицу, можно сделать вывод, что «Пепси» в кувшине, а квас в банке. Получаем новую таблицу:
| Сосуд | Бутылка | Стакан | Кувшин | Банка |
| Жидкость | ||||
| «Пепси» | - | - | + | - |
| «Кока-кола» |
|
| - | - |
| Квас | - | - | - | + |
| «Спрайт» | - |
| - | - |
Теперь можно сказать, что «Спрайт» в стакане, а «Кока-кола» в бутылке.
Ответ. Квас в банке; «Пепси» в кувшине; «Кока-кола» в бутылке; «Спрайт» в стакане.
«Евровидение-2009»
В конкурсе «Евровидение-2009» страны Норвегия, Исландия, Азербайджан и Турция заняли первых четыре места. На следующий день на вопрос, кто какое место занял, представители стран ответили так:
Норвегия: Азербайджан занял первое место;
Исландия: Мы заняли не второе место;
Азербайджан: Турция заняла первое место;
Турция: Мы заняли не четвертое место.
Позже стало известно, что все эти ответы были ложными. Какая страна заняла первое место?
Решение Так как все ответы стран были ложными, то известно, что Азербайджан занял не первое место, Исландия заняла второе место, Турция заняла четвертое место. Внесем эти данные в таблицу:
| Место | I | II | III | IV |
| Страна | ||||
| Норвегия |
| - |
| - |
| Исландия |
| + |
| - |
| Азербайджан | - | - |
| - |
| Турция | - | - | - | + |
Делаем вывод, что Азербайджан занял третье место, а Норвегия – первое место.
Ответ. Норвегия – первое место; Исландия – второе место; Азербайджан – третье место; Турция – четвертое место.
"Виа Гра"
В группе «Виа Гра» поют три девушки: блондинка, рыжая и брюнетка. В клипе «Бриллианты» девушки одеты в белое, красное и черное платья. Интересно, - заметила брюнетка, - что цвета наших с вами волос не соответствуют нашим платьям.
- А ведь верно, но мне подошло бы твое платье, - подтвердила девушка в белом платье.
В какое платье была одета каждая из девушек?
Решение Учитывая условия задачи, получаем следующий граф: 
Используем правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной. Поэтому граф на рисунке будет выглядеть следующим образом:

Теперь можно сделать вывод, что брюнетка в красном платье, блондинка – в черном, а рыжая – в белом. Задача решена.
Ответ. Брюнетка в красном платье, блондинка – в черном, рыжая – в белом.
Задачи на взвешивание
Задачи на взвешивание - достаточно распространённый вид математических задач. В таких задачах от решающего требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов,но и групп элементов между собой.
1. На столе лежит десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В одной из шляп находятся фальшивые монеты. Настоящая весит 10 граммов, а поддельная только 9. В помощь даны весы со шкалой в граммах. Как определить в какой из шляп находятся фальшивые монеты, используя весы только для одного взвешивания? Весы могут взвешивать не более 750 грамм.
Ответ: Легко! Из первой шляпы берем 1 монету, из второй - 2, из третьей - 3 и т.д. Все это взвешиваем и отнимаем результат от идеального веса (в нашем случае 55*10=550 грамм). Получившееся число будет совпадать с номером шляпы с фальшивыми монетами.
2. Имеется 13 монет, из них ровно одна фальшивая, причем неизвестно, легче она настоящих или тяжелее. Требуется найти эту монету за три взвешивания. Весы - стандартные для задач этого типа: две чашечки без гирь.
Ответ: Отложим в сторону тринадцатую монету, а остальные обозначим следующим образом: FAKE MIND CLOT
Теперь взвешиваем одну четверку против другой (буквы обозначают монеты, входящие в каждую четверку): MA DO - LIKE, ME TO - FIND, FAKE - COIN. Теперь совершенно просто найти фальшивую монету, если она входит в эти двенадцать монет. К примеру, если результаты взвешивания были: слева легче, равно, слева легче, то фальшивой может быть только монета "A", которая легче других.
А что если фальшивой окажется все-таки отложенная нами, тринадцатая монета? Все очень просто: в этом случае при всех трёх взвешиваниях весы будут сбалансированы. К сожалению в этом случае нам не узнать легче или тяжелее тринадцатая монета, но в условии такого требования и не было :)
3. У барона Мюнхгаузена есть 8 внешне одинаковых гирек весом 1 г, 2 г, 3 г, ..., 8 г. Он помнит, какая из гирек сколько весит, но граф Склероз ему не верит. Сможет ли барон провести одно взвешивание на чашечных весах, в результате которого будет однозначно установлен вес хотя бы одной из гирь?
Ответ: Да. 7+8 = 1+2+3+4+5, остается 6.
5. Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.
Ответ: Взвешиваешь 50 и 50 монет:
1) Равенство:
Беpем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там
1.1 Левая кучка тяжелее = фальшивая монета тяжелее
1.2 Левая кучка легче = фальшивая монета легче
2) Hеpавенство:
Беpем более тяжелую кучку и разбиваем ее на две кучки по 25 монет.
2.1 Вес кучек одинаковый = фальшивая монета легче
2.2 Вес кучек неодинаковый = фальшивая монета тяжелее
Буратино и Кот Базилио
У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету?
Решение.
Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.
Золушка
Мачеха послала Золушку на рынок. Дала ей девять монет: из них 8 настоящих, а одна фальшивая – она легче чем настоящая. Как найти ее Золушке за два взвешивания?
Решение
Разделим 9 монет на 3 равных кучки. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Остается из трех монет определить более легкую: кладем на чаши весов по 1 монете - фальшивкой является более легкая; если же на весах равенство, то фальшивой является третья монета.
Фальшивая монета
Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Hаходить фальшивую монету не требуется.
Решение
Взвешиваем 50 и 50 монет: два случая.
1 случай. Равенство. Берем оставшуюся монету и ставим ее в левую кучку вместо одной из имеющихся там:
а) Левая кучка тяжелее = фальшивая монета тяжелее;
б) Левая кучка легче = фальшивая монета легче.
2 случай. Неравенство. Берем более тяжелую кучку и разбиваем ее на две кучки по 25 монет:
а) Вес кучек одинаковый = фальшивая монета легче;
б) Вес кучек неодинаковый = фальшивая монета тяжелее.
Фальшивая монета 2
Имеется 8 монет. Одна из них фальшивая и легче настоящей монеты. Определите за 3 взвешивания какая из монет фальшивая.
Решение
Делим монеты на две равные кучки – по 4 монеты в каждой. Взвешиваем. Ту кучку, которая легче, опять делим на две одинаковых кучки – теперь по две монеты в каждой. Взвешиваем. Определяем, какая из них легче. Кладем на чаши весов по 1 монете из этой кучки. Фальшивая та, которая легче. Задача решена.
Фальшивая монета 3
Имеется 10 монет. Одна из них фальшивая и легче настоящей монеты. Как, с помощью чашечных весов без гирь, определить какая из монет фальшивая?
Решение
Разделим 10 монет на 2 равных кучки – по 5 монет. Положим на чаши весов. Определим, в какой из этих кучек находится фальшивая монета. Теперь эту кучку делим на 3 кучки – в двух из них по две монеты, в третьей одна монета. Взвешиваем кучки, в которых по две монеты. Если весы покажут равенство, то фальшивка в третьей кучке. Если покажут неравенство, то фальшивая монета в кучке, которая легче. Теперь кладем на чаши весов по 1 монете из этой кучки – фальшивкой является более легкая. Задача решена.
Лиса Алиса и Кот Базилио
Лиса Алиса и Кот Базилио – фальшивомонетчики. Базилио делает монеты тяжелее настоящих, а Алиса – легче. У Буратино есть 15 одинаковых по внешнему виду монет, но какая-то одна – фальшивая. Как двумя взвешиваниями на чашечных весах без гирь Буратино может определить, кто сделал фальшивую монету – Кот Базилио или Лиса Алиса?
Решение
Буратино может разделить свои монеты на три кучки по 7, 4, 4, или по 5, 5, 5, или по 3, 6, 6, или по 1, 7, 7 монет. При первом взвешивании он положит на весы две кучки монет одинаковой величины. Если при этом весы оказались в равновесии, значит, все монеты на весах настоящие, а бракованная монета в оставшейся кучке. Тогда при втором взвешивании на одну чашку весов Буратино положит кучку с бракованной монетой, а на вторую – столько настоящих монет, сколько всего монет он положил на первую чашку, и тогда он сразу определит, легче фальшивая монета, чем настоящие, или тяжелее. Если же при первом взвешивании весы оказались не в равновесии, значит, все монеты в оставшейся кучке настоящие. Тогда Буратино уберет с весов легкую кучку, а монеты из тяжелой кучки разделит на две равные части и положит на весы (если в кучке было 5 или 7 монет, предварительно добавит к ним одну настоящую монету). Если при втором взвешивании весы оказались в равновесии, значит, фальшивая монета легче настоящих, а если нет, то тяжелее. Задача решена.
Буратино
Буратино имеет четыре одинаковых по виду монеты, одна из которых не золотая, а фальшивая и легче других. Как Буратино определить фальшивую монету? Какое минимальное число взвешиваний ему потребуется?
Решение
Разделим монеты на 2 равных кучки – по 2 монеты. Положим на чаши весов. В более легкой кучке находится фальшивая монета. Теперь кладем на чаши весов по 1 монете из этой кучки – фальшивкой является более легкая. Буратино потребуется два взвешивания. Задача решена.
Дядюшка Скрудж
Дядюшке Скруджу принесли 8 одинаковых по виду монет, одна из которых не золотая, а фальшивая и легче других. Помогите Скруджу определить фальшивую монету. Какое минимальное число взвешиваний ему потребуется?
Решение
Разделим монеты на кучки по 3, 3, 2 монеты. Положим на чаши весов кучки по 3 монеты – по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка.
Если весы покажут равенство, то фальшивая монета в третьей кучке. Тогда кладем на чаши весов монеты из третьей кучки. Фальшивкой будет та, которая легче.
Если весы покажут неравенство. Тогда кладем на чаши весов по монете из более легкой кучки; если установилось равенство, то фальшивкой является третья монета из этой кучки; если неравенство – то более легкая монета и есть фальшивка. Следовательно, Скруджу потребуется минимум два взвешивания. Задача решена.
ЗАДАЧИ НА ПРОЦЕНТЫ
Задача 1. Сколько человек работало на заводе?
В начале года число мужчин, работавших на заводе, составляло 40% от общей численности работников завода. После того, как были приняты на работу еще 6 мужчин, а 5 женщин уволилось, число мужчин и женщин на заводе сравнялось.
Сколько человек работало на заводе в начале года?
РЕШЕНИЕ:
Ч исло мужчин, работавших на заводе в начале года, было на 11 меньше числа работавших там женщин
исло мужчин, работавших на заводе в начале года, было на 11 меньше числа работавших там женщин
Процентная разность между числом женщин и числом мужчин составляла в начале года 20%.
Общая численность работавших на заводе в это время - 11:0,2 = 55 человек.
Задача 2. Сколько процентов составляет возраст сестры?
Возраст брата составляет 40% от возраста сестры.
Сколько процентов составляет возраст сестры от возраста брата?
РЕШЕНИЕ:
П римем возраст сестры за 100%.
римем возраст сестры за 100%.
Возраст брата составит 40%.
Процентное отношение возраста сестры к возрасту брата равно: (100/40) · 100% = 250%.
Задача 3. Как изменилась масса арбуза?
Влажность купленного арбуза составила 99%. В результате длительного хранения влажность снизилась до 98%.
Как изменилась масса арбуза?
РЕШЕНИЕ
С вежий арбуз на 99% процентов состотит из жидкости и на 1% - из сухой массы. В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза.
вежий арбуз на 99% процентов состотит из жидкости и на 1% - из сухой массы. В результате усушки количество жидкости уменьшилось и составило 98% от новой, также уменьшившейся массы арбуза.
Количество же сухого вещества, оставаясь неизменным, составило 2% от новой массы арбуза. Процентное содержание в арбузе сухого вещества (при неизменной его массе) увеличилось вдвое.
Следовательно масса арбуза в результате усушки уменьшилась вдвое.
Задача 4. Сколько времени потребовалось второму путнику ?
Двое путников одновременно вышли из пункта А по направлению к пункту В.
Шаг второго был на 20 % короче, чем шаг первого, но зато второй успевал за то же время сделать на 20% шагов больше, чем первый. Сколько времени потребовалось второму путнику для достижения цели,
если первый прибыл в пункт В спустя 5 часов после выхода из пункта А ?
РЕШЕНИЕ:
Ш аг второго путника составлял 80% или 0,8 шага первого путника.
аг второго путника составлял 80% или 0,8 шага первого путника.
На каждые 100 шагов первого путника второй успевал сделать 120 шагов,
т.е. за то же время второй путник успевал сделать в 1.2 раза больше шагов, чем первый.
Следовательно, расстояние, пройденное за некоторое время вторым путником, составляло 0,8 * 1,2 = 0,96 расстояния, пройденного за то же время первым.
Путь, пройденный телом за некоторое время, прямо пропорционален скорости движения.
Поэтому, скорость второго путника составляла 0,96 скорости первого.
Время, которое затрачивает тело на прохождение определенного пути, обратно пропорционально скорости движения.
Поэтому, продолжительность движения первого путника из А в В составляет 0,96 продолжительности движения второго путника на этой дистанции.
Для перехода из А в В второму путнику потребовалось 5 : 0,96 = 5,2 часа = 5ч 12 мин.
Задачи "на переливание"
|
| 18.03.2012, 19:01 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Задачи на переливание. Задачи "на переливание" более чем увлекательные. Один из методов их решения - "от конца к началу". Нужно исходить из того, что надо получить. Задача 1. Как, пользуясь банками в 3 л и 5 л, набрать воды ровно 1 л? Решение:
Задача 2. Как отмерить 4 л воды с помощью сосудов в 3 л и 5 л? Решение:
Задача 3. Как, имея лишь два сосуда емкостью 5 л и 7 л, отмерить 6 л воды? Решение:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Занимательные олимпиадные задачи по математике: задачи на переливание
Задачи на переливание относятся к олимпиадным номерам, но предлагаются не только сильным ученикам. Интерес к простому условию заставляет школьника среднего уровня способностей активно искать решение на равных с сильным сверстником. Хороший репетитор по математике использует это стремление в 5 — 6 классах для воспитания интереса к предмету. Задачи не имеют возрастных ограничений и представляют собой хорошую головоломку даже для взрослого человека.
Олимпиадные задачи по математике на переливание
1) Имеются два сосуда: один объемом 4 литра, а другой объемом 9 литров. Получится ли с их помощью налить из озера ровно 6 литров воды? Разрешается переливать всю воду из одного сосуда в другой и выливать воду из любого из них обратно в озеро.
2) Богатырь подошел к реке с двумя ведрами, вмещающими 15 литров и 16 литров. Удастся ли ему налить (отмерить) при помощи этих ведер ровно 8 литров воды?
3) Молочница принесла молоко в восьмилитровом ведре, а у бабушки имеется только одна трехлитровая банка и одно четырехлитровое ведро. Как ей взять у молочницы 4 литра молока?
4) Отлейте из бочки ровно 13 литра кваса при помощи двух бидонов: один емкостью 17 литров, а другой емкостью 5 литров.
5) Бочка вмещает 12 ведер воды. Для полива с вечера ее наполнили до верху. Имеются две пустые бочки, вмещающие 5 ведер и 8 ведер воды. Разлейте содержимое бочки поровну.
6) В канистре не менее 10 литров керосина. Можно ли отлить из нее 6 литров керосина, используя девятилитровую и пятилитровую канистру?
7) В бочке не менее 13 ведер воды. Можно ли из нее отлить ровно 8 ведер, если имеются две пустые бочки, вмещающие 9 и 5 ведер?
8) Имеется два полных бидона яблочного сока по 10 литров в каждом. Как налить из них в две пустые кастрюли объемами 4 литра и 5 литров по 2 литра молока?
9) Бидон емкостью 10 литров наполнен квасом. Требуется перелить из него 5 литров в семилитровый бидон, при помощи еще одного трехлитрового бидона. Как это сделать?
10) В шестилитровом ведре 4 литра парного молока, а в семилитровом — 6 литров. Как из шестилитрового ведра вылить ровно 1 литр при помощи еще одной трехлитровой банки?
При пользовании олимпиадных задач на переливание репетитор по математике предоставляет ученикам 5 — 6 классов великолепное средство для развития зрительной памяти, ибо поиск верного хода решения требует визуального контроля сразу нескольких параметров (состояний) сосудов. Если в одном из них находится жидкость, то вместе с объемом налитого приходится помнить еще и об объеме свободной части. А это уже целых 2 параметра.
Чтобы упростить учет всех возможностей по изменению состояний заносим данные об объемах каждого сосуда в специальную таблицу:

В каждую колонку заносим состояния всех сосудов после каждого изменения. От ученика потребуется способность внимательно следить за их параметрами, дабы избежать повторений. Если перебрать все возможные варианты ни разу не повторяясь, то среди них обязательно найдется искомая комбинация.
27












