СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Курс лекций по ЕН.01 Математике специальности 21.02.02 Бурение нефтяных и газовых скважин
Просмотр содержимого документа
«Курс лекций по ЕН.01 Математике специальности 21.02.02 Бурение нефтяных и газовых скважин»
Введение. Функция. Предел функции в точке и на бесконечности.
План
Ввести понятие предела функции в точке;
Рассмотреть геометрическую иллюстрацию понятия предела функции в точке;
Ввести понятие непрерывности функции;
Правила о нахождении предела суммы, произведения и частного двух функций;
Что такое бесконечность;
Предел функции на плюс бесконечности;
Предел функции на минус бесконечности;
Предел функции на бесконечности;
Основные свойства.
Тема нашего урока: «Предел функции в точке». Сегодня на уроке мы познакомимся с понятиями «предел функции в точке», «непрерывность функции», а также рассмотрим правила вычисления предела функции в точке.
- Эта тема очень важна для дальнейшего изучения алгебры: понятие предела функции имеет большое значение для построения графиков функций. Кроме того, в дальнейшем мы будем изучать понятие производной и без знания предела функции рассмотрение этого понятия невозможно.
- Перед тем как начать изучать новую тему выполним следующее задание: постройте график функции 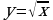 если:
если:
а) при х = 4 значение функции не существует; (рис.1)
б) при х = 4 значение функции равно 3; (рис.2)
в) при х = 4 значение функции равно 2. (рис.3)
Рисунок 1
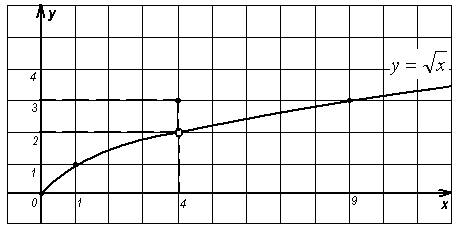
Рисунок 1
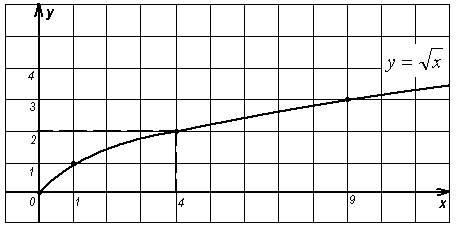
Рисунок 2
- Воспользуемся построенными графиками функций. Во всех трех случаях изображена одна и та же кривая, тем не менее, это три разные функции.
- Чем они отличаются друг от друга?
(Они отличаются друг от друга своим поведением в точке х = 4).
- Как ведет себя функция в точке х = 4 на первом графике?
(Для функции 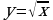 при х = 4 значение функции не существует, функция в указанной точке не определена).
при х = 4 значение функции не существует, функция в указанной точке не определена).
- Как ведет себя функция в точке х = 4 на втором графике?
(Для функции 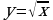 при х = 4 значение функции существует, но оно отличается от естественного значения функции в указанной точке).
при х = 4 значение функции существует, но оно отличается от естественного значения функции в указанной точке).
- Как ведет себя функция в точке х = 4 на третьем графике?
(Для функции 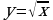 при х = 4 значение функции существует, и оно равно естественному значению функции в указанной точке, то есть двум).
при х = 4 значение функции существует, и оно равно естественному значению функции в указанной точке, то есть двум).
- Если мы исключим точку х = 4 из рассмотрения, то все три функции будут тождественными.
- Для всех трех случаев используется одна и та же запись:  .
.
- В общем случае эта запись выглядит следующим образом: 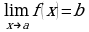 .
.
- Эту запись читаем так: «предел функции y=f(x) при стремлении х к а равен b».
- А теперь ответьте на такой вопрос: какую из трех рассмотренных функций естественно считать непрерывной в точке х = 4?
(Непрерывной будет третья функция)
- Так как эта функция непрерывна, то она удовлетворяет условию 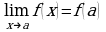 . И функцию f (x) называют непрерывной в точке х = а.
. И функцию f (x) называют непрерывной в точке х = а.
- Иными словами, функцию y = f (x) называют непрерывной в точке х = а, если предел функции y = f (x) при стремлении х к а равен значению функции в точке х = а.
- Функция y = f (x) называется непрерывной на промежутке Х, если она непрерывна в каждой точке промежутка.
Решение задач.
№ 1). Постройте график какой – нибудь функции y = g (x), обладающей заданным свойством:
а) 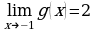 , (рис.4)
, (рис.4)
б) 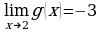 . (рис.5)
. (рис.5)
Решение.
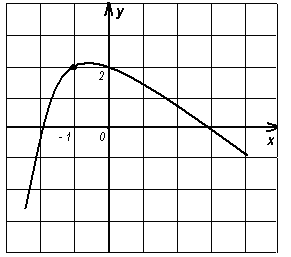
Рисунок 3 Рисунок 4
- Рассмотрим несколько примеров на вычисление пределов функций.
Пример 1. Вычислить: 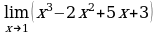 .
.
Решение. Выражение х3 – 2х2 + 5х + 3 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х3 – 2х2 + 5х + 3 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем: 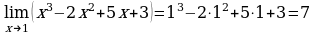 .
.
Ответ: 7.
- Для решения следующего примера нам потребуются правила вычисления предела функции в точке.
Правило 1. 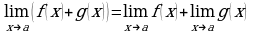 .
.
Правило 2. 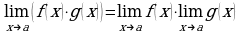 .
.
Правило 3. 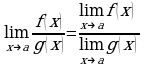 .
.
Пример 2. Используя эти правила, вычислим 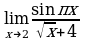 .
.
Решение. Выражение  определено в любой точке х 0, в частности, в точке х = 2. Следовательно, функция у = f (x) непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению функции в точке х = 2. Имеем:
определено в любой точке х 0, в частности, в точке х = 2. Следовательно, функция у = f (x) непрерывна в точке х = 2, а потому предел функции при стремлении х к 2 равен значению функции в точке х = 2. Имеем:  .
.
Ответ: 0.
Пример 3: а) 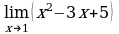 ; б)
; б) 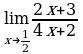 ; в)
; в) 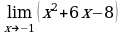 ; г)
; г) 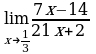 .
.
Решение.
а) 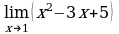 . Выражение х2 – 3х + 5 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х2 – 3х + 5 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
. Выражение х2 – 3х + 5 определено в любой точке х, в частности, в точке х = 1. Следовательно, функция у = х2 – 3х + 5 непрерывна в точке х = 1, а потому предел функции при стремлении х к 1 равен значению функции в точке х = 1.
Имеем: 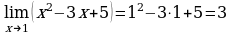 .
.
Ответ: 3.
б) 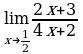 . Выражение
. Выражение 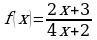 определено в любой точке х
определено в любой точке х 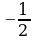 , в частности, в точке х =
, в частности, в точке х = 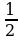 . Следовательно, функция у = f (x) непрерывна в точке х =
. Следовательно, функция у = f (x) непрерывна в точке х = 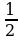 , а потому предел функции при стремлении х к
, а потому предел функции при стремлении х к 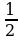 равен значению функции в точке х =
равен значению функции в точке х = 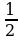 . Имеем:
. Имеем: 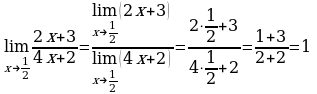 .
.
Ответ: 0.
в) 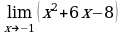 . Выражение х2 + 6х – 8 определено в любой точке х, в частности, в точке х = - 1. Следовательно, функция у = х2 + 6х – 8 непрерывна в точке х = - 1, а потому предел функции при стремлении х к - 1 равен значению функции в точке х = - 1.
. Выражение х2 + 6х – 8 определено в любой точке х, в частности, в точке х = - 1. Следовательно, функция у = х2 + 6х – 8 непрерывна в точке х = - 1, а потому предел функции при стремлении х к - 1 равен значению функции в точке х = - 1.
Имеем: 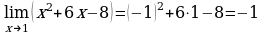 .
.
Ответ: - 1.
г) 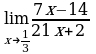 . Выражение
. Выражение  определено в любой точке х
определено в любой точке х  , в частности, в точке х =
, в частности, в точке х = 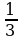 . Следовательно, функция у = f (x) непрерывна в точке х =
. Следовательно, функция у = f (x) непрерывна в точке х = 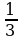 , а потому предел функции при стремлении х к
, а потому предел функции при стремлении х к 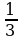 равен значению функции в точке х =
равен значению функции в точке х = 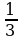 .
.
Имеем: 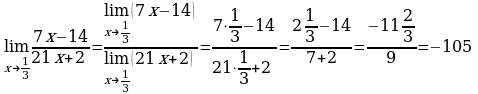 .
.
- Вы заметили, что в рассмотренных примерах вычисление пределов не составило значительных сложностей: достаточно было найти значение функции в точке, к которой стремится аргумент х. Но часты случаи, когда этот прием не срабатывает.
Пример 4. Вычислить 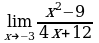 .
.
Решение. Если подставить значение х = - 3 в заданное выражение, то и в числителе, и в знаменателе получится 0, а на нуль делить нельзя. Но заданную алгебраическую дробь можно сократить:  .
.
Значит, функции 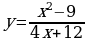 и
и  тождественны при условии х - 3. Но при вычислении предела функции при х - 3 саму точку х = - 3 можно исключить из рассмотрения. Значит,
тождественны при условии х - 3. Но при вычислении предела функции при х - 3 саму точку х = - 3 можно исключить из рассмотрения. Значит, 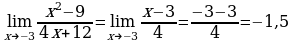 .
.
Ответ: - 1,5.
Ребята, давайте посмотрим, что такое предел функции на бесконечности?
А, что такое бесконечность?
Бесконечность — используется для характеристики безграничных, беспредельных, неисчерпаемых предметов и явлений, в нашем случае характеристика чисел.
Бесконечность –сколь угодно большое(малое), безграничное число.
Если рассмотреть координатную плоскость то ось абсцисс(ординат) уходит на бесконечность, если ее безгранично продолжать влево или вправо(вниз или вверх).
Предел функции на плюс бесконечности.
Т еперь давайте перейдем к пределу функции на бесконечности:
еперь давайте перейдем к пределу функции на бесконечности:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч [a; +∞), и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке: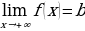 .
.
Будем читать наше выражение как: предел функции y=f(x) при x стремящимся к плюс бесконечности равен b.(рисунок 1)
Р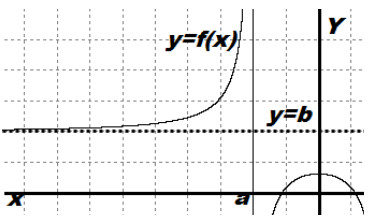 ис. 1
ис. 1
Предел функции на минус бесконечности.
Посмотрим немного другой случай:
Пусть у нас есть функция y=f(x), область определения нашей функции содержит луч (-∞; a], и пусть прямая y=b является горизонтальной асимптотой графика функции y=f(x), запишем все это на математическом языке: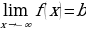 .
.
Будем читать наше выражение как: предел функции y=f(x) при x стремящимся к минус бесконечности равен b.(рисунок 2)
Рис. 2
Предел функции на бесконечности.
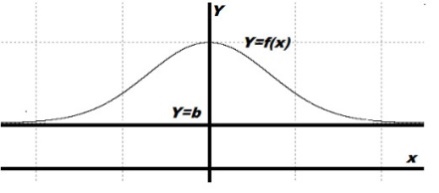 Так же наши соотношения могут выполняться одновременно. Тогда принято записывать как:
Так же наши соотношения могут выполняться одновременно. Тогда принято записывать как: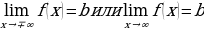 .
.
Будем читать наше выражение как: предел функции y=f(x) при x стремящимся к бесконечности равен b. (рисунок 3)
Рис. 3
Пример 5.
Построить график функции y=f(x), такой что:
1) Область определения – множество действительных чисел.
2) f(x)- непрерывная функция
3)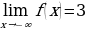
4)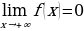
Решение: Нам надо построить непрерывную функцию на (-∞; +∞). Покажем пару примеров нашей функции.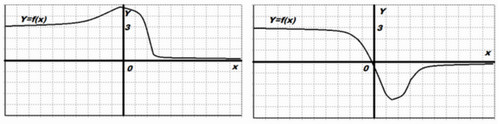
Основные свойства
Для вычисления предела на бесконечности пользуются несколькими
1) Для любого натурально числа m справедливо следующее соотношение: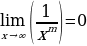
2) Если 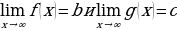 то:
то:
а) Предел суммы равен сумме пределов: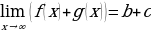
б) Предел произведения равен произведению пределов: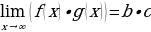
в) Предел частного равен частному пределов: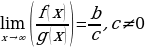
г) Постоянный множитель можно вынести за знак предела: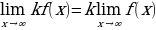
Пример 6
Найти .
.
Решение:
Разделим числитель и знаменатель дроби на x.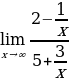 .
.
Воспользуемся свойством предел частного равен частному пределов: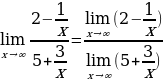 .
.
Ребята, вспомните предел числовой последовательности. 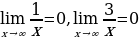 .
.
Получим: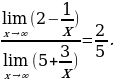
Пример 7
Найти предел функции y=f(x), при x стремящимся к бесконечности. Если 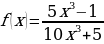 .
.
Решение: 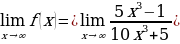 . Разделим числитель и знаменатель дроби на x в третьей степени
. Разделим числитель и знаменатель дроби на x в третьей степени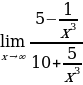 . Воспользуемся свойствами предела на бесконечности
. Воспользуемся свойствами предела на бесконечности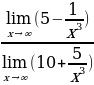 . Предел числителя равен: 5-0=5. Предел знаменателя равен: 10+0=10
. Предел числителя равен: 5-0=5. Предел знаменателя равен: 10+0=10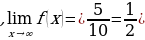 .
.
Пример 8
Найти предел функции y=f(x), при x стремящимся к бесконечности.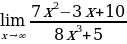 .
.
Разделим числитель и знаменатель дроби на x в третьей степени.
Воспользуемся свойствами предела на бесконечности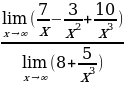 .
.
Предел числителя равен: 0; Предел знаменателя равен: 8. 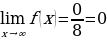 .
.
Производная. Основные формулы и правила дифференцирования.
План:
1. Скорость изменения функции. Определение производной.
2. Нахождение производной по общему правилу.
3. Механический смысл.
4. Геометрический смысл.
5. Формулы дифференцирования.
6. Основные правила дифференцирования.
7.Дифференцирование функции 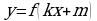 .
.
Опр. 1 Пусть функция 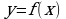 определена в точке
определена в точке  и в некоторой ее окрестности. Дадим аргументу
и в некоторой ее окрестности. Дадим аргументу  приращение
приращение 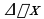 , такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращении функции
, такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращении функции 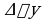 и составим отношение
и составим отношение  Если существует предел этого отношения при
Если существует предел этого отношения при 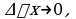 то указанный предел называют производной функции
то указанный предел называют производной функции 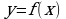 в точке
в точке  и обозначают
и обозначают 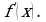
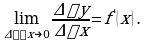
Для обозначения часто используют символ 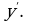
Отметим, что 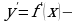 это новая функция, но, естественно, связанная с функцией
это новая функция, но, естественно, связанная с функцией 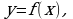 определенная во всех таких точках
определенная во всех таких точках 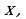 в которых существует указанный выше предел. Эту функцию называют так: производная функции
в которых существует указанный выше предел. Эту функцию называют так: производная функции 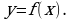
Для линейной функции 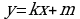 справедливо равенство
справедливо равенство 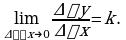
Это означает, что 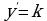 или, подробнее,
или, подробнее,
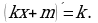
В частности,

Для функции 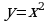 справедливо равенство
справедливо равенство 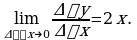
Это означает, что  или, подробнее,
или, подробнее,

Физический (механический) смысл производной состоит в следующем. Если 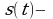 закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени
закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени 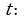
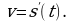
На практике во многих отраслях науки используется обобщение полученного равенства: если некоторый процесс протекает по закону 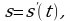 то производная
то производная 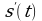 выражает скорость в момент времени
выражает скорость в момент времени 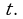
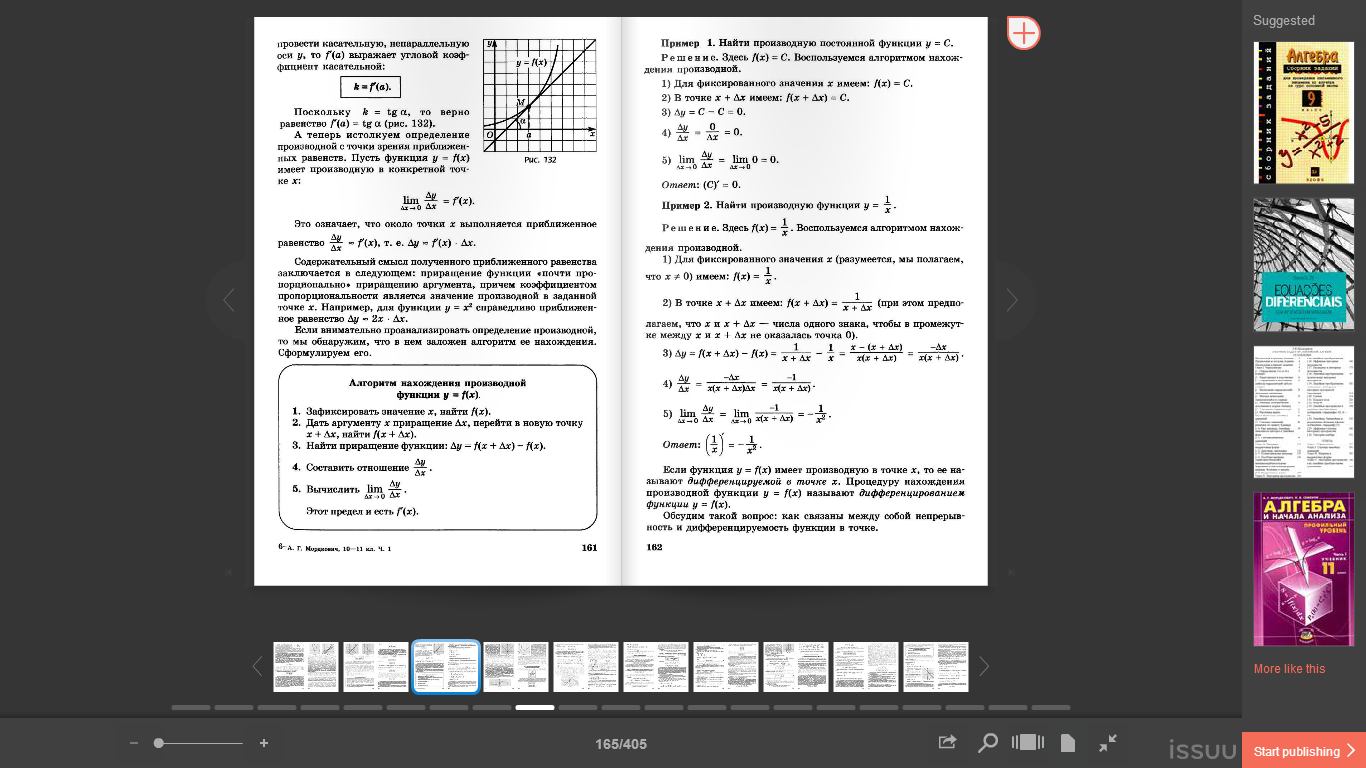
Геометрический смысл производной состоит в следующем. Если к графику функции 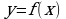 в точке с абсциссой
в точке с абсциссой 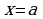 можно провести касательную, непараллельную оси
можно провести касательную, непараллельную оси 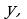
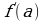 выражает угловой коэффициент касательной:
выражает угловой коэффициент касательной:
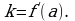
Поскольку  то верно равенство
то верно равенство 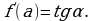
Формулы дифференцирования.
Формулами дифференцирования обычно называют формулы для отыскания производных конкретных функций, например:
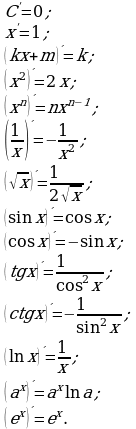
Пример 1. Найти значение производной данной функции в данной точке:
а) 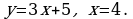
Решение:  значит, производная равна 3 в любой точке
значит, производная равна 3 в любой точке 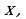 в частности в заданной точке
в частности в заданной точке 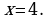 Принято записывать так:
Принято записывать так: 
б) 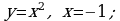
в) 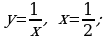
г) 
Пример 2. Составить уравнение касательной к графику функции 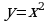 в точке
в точке 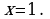
Решение: Уравнение касательной, как уравнение всякой прямой, имеет вид 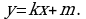 Найдем сначала
Найдем сначала 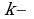 это угловой коэффициент касательной, который, как мы знаем, равен
это угловой коэффициент касательной, который, как мы знаем, равен 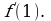
Имеем 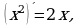 значит,
значит, 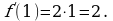
Итак, 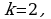 т. е. уравнение касательной надо искать в виде
т. е. уравнение касательной надо искать в виде 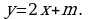
Найдем значение коэффициента 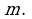 Для этого воспользуемся тем, что касательная проходит через точку на параболе
Для этого воспользуемся тем, что касательная проходит через точку на параболе 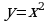 c абсциссой
c абсциссой 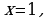 т.е. через точку
т.е. через точку 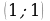 . Подставим
. Подставим 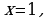
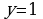 в уравнение
в уравнение 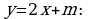
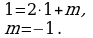
Итак, уравнение касательной имеет вид 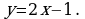
Основные правила дифференцирования
Правило 1. Если функция 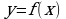 и
и  имеют производную в точке
имеют производную в точке  то и их сумма имеет производную в точке
то и их сумма имеет производную в точке 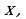 причем производная суммы равна сумме производных:
причем производная суммы равна сумме производных:
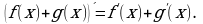
Производная суммы равна сумме производных.
Например, 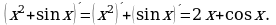
Правило 2. Если функция 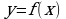 имеет производную в точке
имеет производную в точке 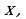 то и функция
то и функция 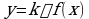 имеет производную в точке
имеет производную в точке 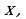 причем
причем
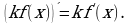
Постоянный множитель можно вынести за знак производной.
Например,

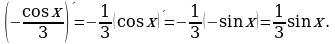
Правило 3. Если функции 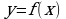 и
и  имеют производную в точке
имеют производную в точке 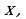 то и их произведение имеет производную в точке
то и их произведение имеет производную в точке 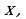 причем
причем
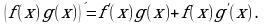
Производная произведения двух функций равна сумме двух слагаемых; первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Например,
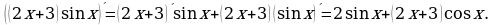
Правило 4. Если функции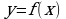 и
и  имеют производную в точке
имеют производную в точке  и в этой точке
и в этой точке 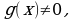 то и частное
то и частное 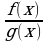 имеют производную в точке
имеют производную в точке 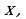 причем
причем
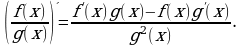
Например,
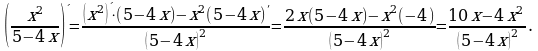
Дифференцирование функции 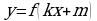 .
.
Теорема. Производная функции 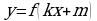 вычисляется по формуле
вычисляется по формуле
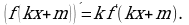
Пример 5. Найти значение производной функции 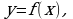 где
где 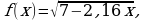 в точке
в точке 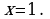
Решение: Сначала найдем производную в произвольной точке 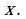 Известно, что
Известно, что  По этой формуле найдем интересующую нас производную, но при этом учтем два обстоятельства:
По этой формуле найдем интересующую нас производную, но при этом учтем два обстоятельства:
Под знаком корня напишем не 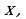 а
а 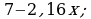
Укажем дополнительный множитель, равный 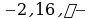 это коэффициент при
это коэффициент при 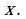 Таким образом,
Таким образом,

Чтобы вычислить  в полученное выражение подставим
в полученное выражение подставим 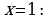
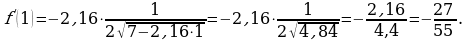
№1. Найдите производные следующих функций.
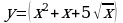 ;
;
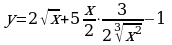 ;
;
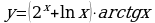 ;
;
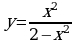 ;
;
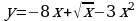 ;
;
 ;
;
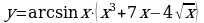 ;
;
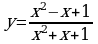 ;
;
 ;
;
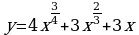 ;
;
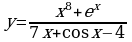 .
.
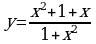 ;
;
№2.Составить уравнение касательной и нормали к графику функции в точке 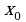 .
.
а) 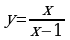
![]() ;
;
б) 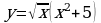
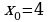 ;
;
в) 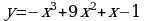
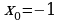 .
.
№3. Точка движется по закону 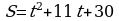 . Найдите значение скорости в момент времени
. Найдите значение скорости в момент времени 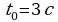 .
.
Наибольшее и наименьшее значение функции.
План:
Экстремумы функции.
Правила нахождения экстремумов функции.
Наименьшее и наибольшее значения.
Экстремумы функции.
Точка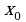 из области определения функции
из области определения функции 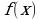 называется точкой минимума этой функции, если существует такая
называется точкой минимума этой функции, если существует такая  окрестность
окрестность  точки
точки 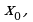 что для всех
что для всех 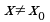 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 
Точка 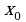 из области определения функции
из области определения функции 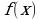 называется точкой максимума этой функции, если существует такая
называется точкой максимума этой функции, если существует такая  окрестность
окрестность  точки
точки 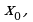 что для всех
что для всех 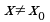 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 
Точки минимума и максимума функции называются экстремальными точками (или точками экстремума) данной функции, а значения функции в этих точках- минимумом и максимумом (или экстремумами) функции.
Точками экстремума могут служить только критические точки, т.е. точки, принадлежащие области определения функции, в которых производится 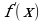 обращается в ноль или терпит разрыв.
обращается в ноль или терпит разрыв.
Если при переходе через критическую точку 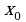 производная
производная 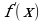 меняет знак, то функция
меняет знак, то функция 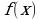 имеет значение в точке
имеет значение в точке 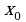 экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум- когда с плюса на минус. Если же при переходе через критическую
экстремум: минимум в том случае, когда производная меняет знак с минуса на плюс, и максимум- когда с плюса на минус. Если же при переходе через критическую 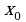 производная
производная 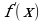 не меняет знака, то функция
не меняет знака, то функция 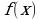 в точке
в точке 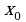 не имеет экстремума.
не имеет экстремума.
Правило нахождения экстремумов функции 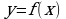 с помощью первой производной
с помощью первой производной
Найти производную 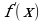 .
.
Найти критические точки функции 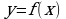 , т.е. точки, в которых
, т.е. точки, в которых 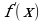 обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Исследовать знак производной 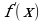 в промежутках, на которые найденные критические точки делят область определения функции
в промежутках, на которые найденные критические точки делят область определения функции 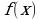 . При этом критическая точка
. При этом критическая точка 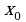 есть точка минимума, если она отделяет промежуток, в котором
есть точка минимума, если она отделяет промежуток, в котором 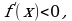 от промежутка, в котором
от промежутка, в котором 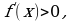 и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой
и точка максимума – в противном случае. Если же в соседних промежутках, разделенных критической точкой 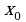 , знак производной не меняется, то в точке
, знак производной не меняется, то в точке 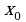 функция экстремума не имеет.
функция экстремума не имеет.
Вычислить значения функции в точках экстремума.
Пример 1. Исследовать на экстремум функцию 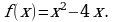
Находим 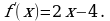 Полагая что
Полагая что 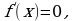 получим единственную критическую точку
получим единственную критическую точку 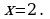 Дальнейшие рассуждения представлены в таблице:
Дальнейшие рассуждения представлены в таблице:
|
|
|
|
|
|
|
|
|
|
|
|
| Минимум
|
|

y

x
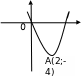
График функции  есть парабола, изображенная на рисунке. Точка минимума
есть парабола, изображенная на рисунке. Точка минимума 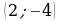 является вершиной параболы.
является вершиной параболы.
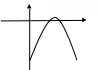
Пример 2. Исследовать на экстремум функцию 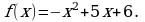
Находим 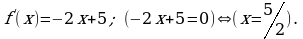 Составим таблицу:
Составим таблицу:
|
|
|
|
|
|
|
|
|
|
|
y 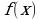 |
| Максимум
|
|

0

x
Графиком функции  служит парабола, изображенная на рисунке.
служит парабола, изображенная на рисунке.
Наименьшее и наибольшее значение функции
Для нахождения наименьшего и наибольшего значений функции, непрерывной в некотором промежутке, необходимо:
Найти критические точки, принадлежащие заданному промежутку, и вычислить значения функции в этих точках;
Найти значения функции на концах промежутка;
Сравнить полученные значения; тогда наименьшее и наибольшее из них являются соответственно наименьшим и наибольшим значениями функции в рассматриваемом промежутке.
Пример 3. Найти наименьшее и наибольшее значения функции 
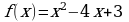 в промежутке
в промежутке 
Имеем 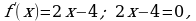 т.е.
т.е.  критическая точка. Находим
критическая точка. Находим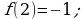
далее, вычисляем значения функции на концах промежутка: 
Итак, наименьшее значение функции равно -1 и достигается ею во внутренней точке промежутка, а наибольшее значение равно 3 и достигается на левом конце промежутка.
Пример 4. а) Найти точки экстремума функции
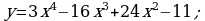
б) построить график этой функции.
Решение. а) Найдем производную данной функции:
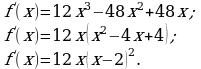
![]() Производная обращается в нуль в точках
Производная обращается в нуль в точках 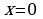 и
и  это две стационарные точки заданной функции. На рисунке схематически указаны знаки производной по промежуткам область определения: на промежутке
это две стационарные точки заданной функции. На рисунке схематически указаны знаки производной по промежуткам область определения: на промежутке 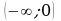 производная отрицательна, на промежутке
производная отрицательна, на промежутке 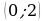 - положительна, на промежутке
- положительна, на промежутке 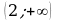 - положительна. Значит,
- положительна. Значит, 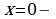 точка минимума функции, а
точка минимума функции, а 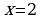 точкой экстремума не является. На первом из указанных выше промежутков функция убывает, на втором и третьем- возрастает.
точкой экстремума не является. На первом из указанных выше промежутков функция убывает, на втором и третьем- возрастает.
В точке минимума 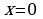 имеем
имеем 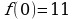 (подставили значение
(подставили значение 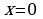 в аналитическое задание функции), значит,
в аналитическое задание функции), значит, 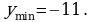
б) Чтобы построить график функции, нужно знать особо важные точки графика. К таковым относятся:
- найденная точка минимума 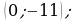
- стационарная точка 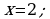 в этой точке
в этой точке 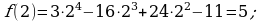
 - точки пересечения графика с осями координат; в данном примере это уже найденная точка
- точки пересечения графика с осями координат; в данном примере это уже найденная точка 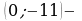 точка пересечения графика с осью
точка пересечения графика с осью 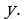 И еще: можно догадаться, что
И еще: можно догадаться, что 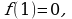 значит найдена точка пересечения графика с осью
значит найдена точка пересечения графика с осью 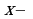 это точка
это точка 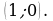
Итак, мы имеем точку минимума 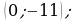 точку пересечения графика с осью
точку пересечения графика с осью 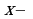 точку
точку 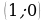 и стационарную точку
и стационарную точку 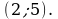 В точке
В точке 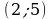 касательная к графику функции горизонтальна, не это не точка экстремума, а точка перегиба.
касательная к графику функции горизонтальна, не это не точка экстремума, а точка перегиба.
График функции схематически изображен на рисунке. Заметим, что есть еще одна точка пересечения графика с осью абсцисс, найти нам ее не удалось. Завершая этот пункт, заметим, что мы фактически выработали
АЛГОРИТМ ИССЛЕДОВАНИЯ НЕПРЕРЫВНОЙ ФУНКЦИИ 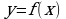 НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ
НА МОНОТОННОСТЬ И ЭКСТРЕМУМЫ
Найти производную 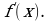
Найти стационарные и критические точки.
Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
Опираясь на вышеуказанные теоретические сведения, сделать выводы о монотонности функции и ее точках экстремумах.
Пример 5. Исследовать функцию  на монотонность и экстремумы.
на монотонность и экстремумы.
Решение. Заметим, что функция всюду непрерывна, кроме точки 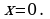 Воспользуемся указанными выше алгоритмом.
Воспользуемся указанными выше алгоритмом.
Найдем производную данной функции:
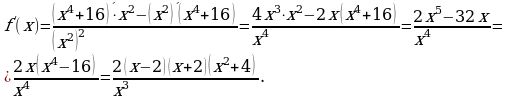
Производная обращается в ноль в точках 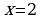 и
и 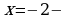 это стационарные точки. Производная не существует в точке
это стационарные точки. Производная не существует в точке 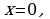 но это не критическая точка, это точка разрыва функции.
но это не критическая точка, это точка разрыва функции.
О тметим точки -2, 0 и 2 на числовой прямой и расставим знаки производной на получившихся промежутках.
тметим точки -2, 0 и 2 на числовой прямой и расставим знаки производной на получившихся промежутках.
Делаем выводы: на луче 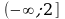 функция убывает, на полуинтервале
функция убывает, на полуинтервале 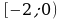 функция возрастает, на полуинтервале
функция возрастает, на полуинтервале 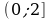 функция убывает, на луче
функция убывает, на луче 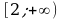 функция возрастает.
функция возрастает.
Далее, 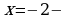 точка минимума, причем
точка минимума, причем 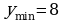 (подставили значение
(подставили значение  в формулу
в формулу  ). Аналогично устанавливаем, что и
). Аналогично устанавливаем, что и 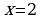 - точка минимума, причем
- точка минимума, причем 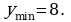
Интеграл. Правила, формулы и методы вычисления интегралов.
План:
Вступление.
Понятие первообразной.
Таблица первообразной.
Интегрирование методом замены переменной.
Интегрирование по частям.
Свойство 1.
Свойство 2.
Свойства 3.
На предыдущих занятиях мы по заданной функции, руководствуясь определенными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: производная– это скорость движения (или, обобщая, скорость протекания любого процесса); производная– это угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремуму; производная помогает решать задачи на оптимизацию.
Но в реальной жизни приходится решать и обратные задачи: например, наряду с задачей об отыскании скорости по известному закону движения встречается и задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.
Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени  задается формулой
задается формулой 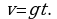 Найти закон движения.
Найти закон движения.
Решение. Пусть 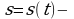 искомый закон движения. Известно, что
искомый закон движения. Известно, что  Значит, для решения задачи нужно подобрать функцию
Значит, для решения задачи нужно подобрать функцию 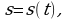 производная которой равна
производная которой равна 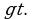 Нетрудно догадаться, что
Нетрудно догадаться, что 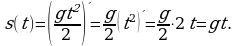
Ответ: 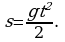
Сразу отметим, что пример решен верно, но неполно. Мы получили, что 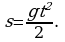 На самом деле задача имеет бесконечно много решений: любая функция вида
На самом деле задача имеет бесконечно много решений: любая функция вида 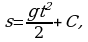 где
где 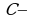 произвольная константа, может служить законом движения, поскольку
произвольная константа, может служить законом движения, поскольку

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при 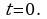 Если, скажем,
Если, скажем, 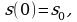 то из равенства
то из равенства 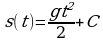 получаем
получаем 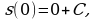 т.е.
т.е. 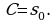 Теперь закон движения определен однозначно:
Теперь закон движения определен однозначно: 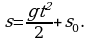
Процесс отыскания производной по заданной функции называют дифференцированием, а обратную операцию, т.е. процесс отыскания функции по заданной производной- интегрированием.
Определение 1. Функцию 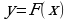 называют первообразной для функции
называют первообразной для функции 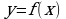 на заданном промежутке
на заданном промежутке  если для всех
если для всех  из
из  выполняется равенство
выполняется равенство 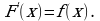
| Функция | Первообразная |
| 0 |
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечания: 1. Если 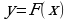 - первообразная для функции
- первообразная для функции 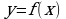 , то функции
, то функции 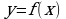 бесконечно много первообразных и все они имеют вид
бесконечно много первообразных и все они имеют вид 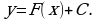 Поэтому правильней было во втором столбце таблицы всюду добавить слагаемое
Поэтому правильней было во втором столбце таблицы всюду добавить слагаемое 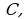 где
где 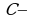 произвольное действительное число.
произвольное действительное число.
2. Ради краткости иногда вместо фразы «функция 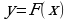 является первообразной для функции
является первообразной для функции 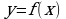 », говорят «
», говорят «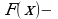 первообразная для
первообразная для 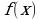 ».
».
Интегрирование методом замены переменной
Сущность интегрирования методом замены переменной (способом подстановки) заключается в преобразовании интеграла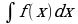 в интеграл
в интеграл 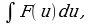 который легко вычисляется по какой-либо из основных формул интегрирования.
который легко вычисляется по какой-либо из основных формул интегрирования.
Для нахождения интеграла 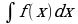 заменяем переменную
заменяем переменную  новой переменной
новой переменной 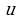 с помощью подстановки
с помощью подстановки  Дифференцируя это равенство, получим
Дифференцируя это равенство, получим 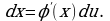 Подставляя в подынтегральное выражение вместо
Подставляя в подынтегральное выражение вместо  и
и 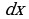 их значения, выраженные через
их значения, выраженные через 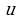 и
и  имеем
имеем
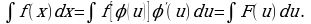
После того как интеграл относительно новой переменной 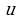 будет найден, с помощью подстановки
будет найден, с помощью подстановки 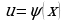 приводится к переменной
приводится к переменной  .
.
Пример 2. Найти следующий интеграл 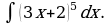
Решение. Введем подстановку 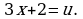 Дифференцируя, имеем
Дифференцируя, имеем 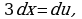 откуда
откуда 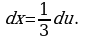 Подставив в данный интеграл вместо
Подставив в данный интеграл вместо 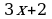 и
и 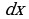 их выражения, получим
их выражения, получим
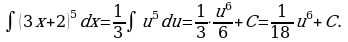
Заменив 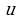 его выражением через
его выражением через  , находим
, находим

Интегрирование по частям
Интегрируя обе части равенства  получим
получим

отсюда

C помощью этой формулы вычисление интеграла 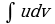 сводится к вычислению интеграла
сводится к вычислению интеграла 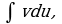 если последний окажется проще исходного.
если последний окажется проще исходного.
Пример 3. Найти интеграл 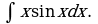
Решение. Положим 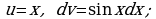 тогда
тогда  т.е.
т.е. 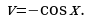 Используя формулу (1), получим
Используя формулу (1), получим

Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл – одно из основных понятий математического анализа. Геометрический смысл интеграла – площадь криволинейной трапеции. Физический смысл интеграла – масса неоднородного стержня с плотностью, перемещение точки, движущейся по прямой со скоростью за промежуток времени.
Опираясь на формулу Ньютона-Лейбница, нетрудно обосновать некоторые свойства определенного интеграла.
Свойство 1. Интеграл от суммы функций равен сумме интегралов:
 =
=  +
+ 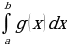 .
.
Доказательство. Если 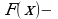 первообразная для
первообразная для 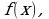 а
а 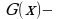 первообразная для
первообразная для 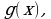 то
то 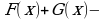 первообразная для
первообразная для 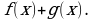 Тогда
Тогда
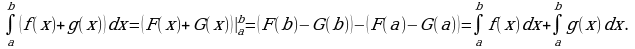
Свойство 2. Постоянный множитель можно вынести за знак интеграла:
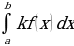 = k
= k .
.
 Свойство 3. Функция у = f(x) определена и непрерывна на отрезке [a; b], причем точка с − внутренняя точка отрезка [a; b] (рис. 2). Имеет место соотношение:
Свойство 3. Функция у = f(x) определена и непрерывна на отрезке [a; b], причем точка с − внутренняя точка отрезка [a; b] (рис. 2). Имеет место соотношение:
 =
= 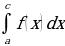 +
+ 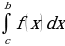 .
.
Доказательство.
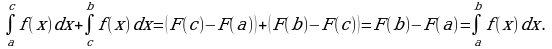
Пример 1. Вычислить определенный интеграл:
а) 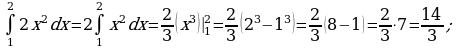
б)  для самостоятельного решения;
для самостоятельного решения;
в) 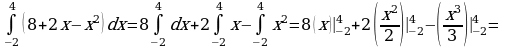
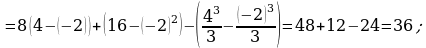
г) 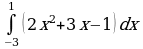 для самостоятельного решения;
для самостоятельного решения;
д)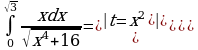
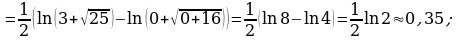
е) 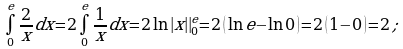
ж)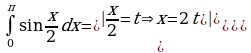
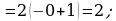
з) 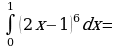 внесем
внесем  под знак дифференциала, тогда
под знак дифференциала, тогда 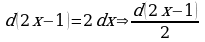 Подставляя все в исходный интеграл, получим:
Подставляя все в исходный интеграл, получим:

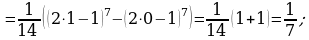
Карточки для самостоятельного решения:
| 1) | 2) | 3) |
| 4) | 5) | 6) |
| 7) | 8) | 9) |
| 10) | 11) | 12) |
| 13) | 14) | 15) |
| 16) | 17) | 18) |
| 19) | 20) | 21) |
| 22) | 23) | 24) |
| 25) | 27) | 28) |
Числовые последовательности и ряды.
План:
1. Определение числовой последовательности и способы их задания
2. Свойства числовых последовательностей
3. Определение предела последовательности.
4. Свойства сходящихся последовательностей
5. Вычисление пределов последовательностей.
6. Степенной ряд.
7. Признак Даламбера.
8. Примеры.
9. Разложение элементарных функций в ряд Маклорена.
Определение 1. Функцию вида 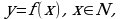 называют функцию натурального аргумента или числовой последовательностью и обозначают
называют функцию натурального аргумента или числовой последовательностью и обозначают 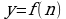 или
или 
Иногда для обозначения последовательности используется запись 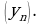
Последовательности можно задавать различными способами, например, словесно, когда правила задания последовательности описано словами, без указания каких-то формул. Так, словесно задается последовательность простых чисел:

Особенно важны аналитически и рекуррентный способы задания последовательности.
Говорят, что последовательность задана аналитически, если указана формула ее n-го члена.
Приведем три примера.
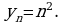 Это аналитическое задание последовательности
Это аналитическое задание последовательности

Указав конкретное значение n, нетрудно найти член последовательности соответствующим номером. Если, например,  то
то 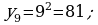 если
если  то
то 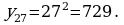 Напротив, если взят определенный член последовательности, можно указать его номер. Например, если взят определенный член последовательности, можно указать его номер. Например, если
Напротив, если взят определенный член последовательности, можно указать его номер. Например, если взят определенный член последовательности, можно указать его номер. Например, если 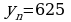 находим, что
находим, что  Это значит, что 25-й член заданной последовательности равен 625.
Это значит, что 25-й член заданной последовательности равен 625.
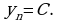 Здесь речь идет о последовательности
Здесь речь идет о последовательности
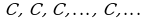
Такую последовательность называют постоянной (или стационарной).
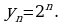 Это аналитическое задание последовательности
Это аналитическое задание последовательности
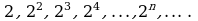
Рекуррентный способ задания числовой последовательности состоит в том, что указывают правило, позволяющее вычислить 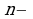 й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия- это числовая последовательность
й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия- это числовая последовательность 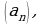 заданная рекуррентно соотношениями
заданная рекуррентно соотношениями
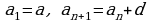
(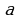 и
и 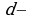 заданные числа,
заданные числа, 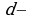 разность арифметической прогрессии).
разность арифметической прогрессии).
Геометрическая прогрессия- это числовая последовательность 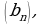 заданная рекуррентными соотношениями
заданная рекуррентными соотношениями

(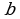 и
и  заданные числа,
заданные числа,  знаменатель геометрической прогрессии).
знаменатель геометрической прогрессии).
Свойства числовых последовательностей
Числовая последовательность- частный случай числовой функции, а потому некоторые свойства функций (ограниченность, монотонность) рассматривают и для последовательностей.
Определение 2. Последовательность 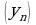 называют ограниченной сверху, если все ее члены не больше некоторого числа.
называют ограниченной сверху, если все ее члены не больше некоторого числа.
Иными словами, последовательность 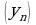 ограничена сверху, если существует число
ограничена сверху, если существует число  такое, что для любого
такое, что для любого 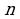 выполняется неравенство
выполняется неравенство  Число
Число 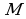 называют верхней границей последовательности.
называют верхней границей последовательности.
Например, последовательность 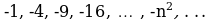 ограниченна сверху. В качестве верхней ограниченна сверху. В качестве верхней границы можно взять число -1 или любое число, которое больше, чем -1, например, 0.
ограниченна сверху. В качестве верхней ограниченна сверху. В качестве верхней границы можно взять число -1 или любое число, которое больше, чем -1, например, 0.
Определение 3. Последовательность 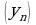 называют ограниченной снизу, если все ее члены не меньше некоторого числа.
называют ограниченной снизу, если все ее члены не меньше некоторого числа.
Иными словами, последовательность 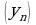 ограничена снизу, если существует число
ограничена снизу, если существует число 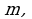 такое, что для любого
такое, что для любого 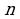 выполняется неравенство
выполняется неравенство 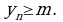 Число
Число 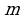 называют нижней границей последовательности.
называют нижней границей последовательности.
Например, последовательность 1, 4, 9, 16, …, 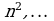 ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1.
ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1.
Если последовательность ограничена и сверху, и снизу, то ее называют ограниченной. Например, последовательность,  ограничена и сверху, и снизу. В качестве верхней границы можно взять 1, в качестве нижней- 0.
ограничена и сверху, и снизу. В качестве верхней границы можно взять 1, в качестве нижней- 0.
Особенно наглядным становится свойство ограниченности последовательности, если члены последовательности отметить точками на числовой прямой. Ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку.
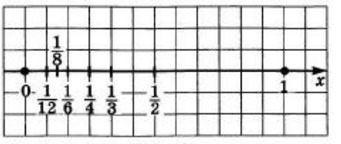
Так, изобразив члены последовательности 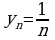 точками на числовой прямой, замечаем, что все они принадлежат отрезку
точками на числовой прямой, замечаем, что все они принадлежат отрезку 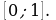
Определение 4. Последовательность 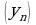 называют возрастающей, если каждый ее член больше предыдущего:
называют возрастающей, если каждый ее член больше предыдущего:
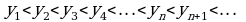
Например, 1, 3, 5, 7, …, 2n-1, ... - возрастающая последовательность.
Определение 5. Последовательность 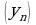 называют убывающей, если каждый ее член меньше предыдущего:
называют убывающей, если каждый ее член меньше предыдущего:
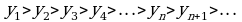
Например,  убывающая последовательность.
убывающая последовательность.
Возрастающие и убывающие последовательности объединяют одним общим термином- монотонные последовательности.
Приведем еще несколько примеров.
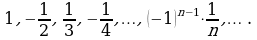 Эта последовательность не является ни возрастающей,
Эта последовательность не является ни возрастающей,
ни убывающей (немонотонная последовательность).
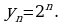 Речь идет о последовательности 2, 4, 8, 16, 32, … . Это возрастающая
Речь идет о последовательности 2, 4, 8, 16, 32, … . Это возрастающая
последовательность.
Вообще если 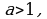 то последовательность
то последовательность  возрастает.
возрастает.
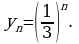 Речь идет о последовательности
Речь идет о последовательности 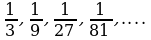 Это убывающая
Это убывающая
последовательность.
Вообще если 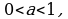 то последовательность
то последовательность  убывает.
убывает.
Определение предела последовательности
Рассмотрим две числовые последовательности 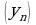 и
и 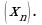
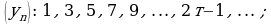

Изобразим члены этих последовательностей точками на координатной прямой. Замечаем, что члены последовательности 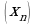 как бы «сгущаются» около точки 0, а у последовательности
как бы «сгущаются» около точки 0, а у последовательности 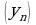 такой «точки сгущения» нет. В подобных случаях математики говорят так: последовательность
такой «точки сгущения» нет. В подобных случаях математики говорят так: последовательность 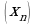 сходится, а последовательность
сходится, а последовательность 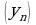 расходится.
расходится.

Возникает естественный вопрос: как узнать, является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности. Чтобы ответить на этот вопрос, введем новый математический термин.
Определение 6. Пусть 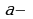 точка прямой, а
точка прямой, а  положительное число. Интервал
положительное число. Интервал 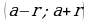 называют окрестностью точки
называют окрестностью точки 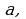 а число
а число  радиусом окрестности.
радиусом окрестности.

Например, (5,98; 6,02)- окрестность точки 6, причем радиус этой окрестности 0,02.
Определение 7. Число 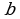 называют пределом последовательности
называют пределом последовательности 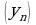 , если в любой заранее выбранной окрестности точки
, если в любой заранее выбранной окрестности точки 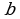 содержаться все члены последовательности, начиная с некоторого номера.
содержаться все члены последовательности, начиная с некоторого номера.
Пишут либо так: 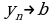 (читают:
(читают: 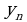 стремится к
стремится к 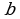 или
или 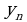 сходится к
сходится к 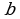 ), либо так:
), либо так: 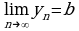 (читают: предел последовательности
(читают: предел последовательности 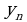 при стремлении
при стремлении 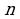 к бесконечности равен
к бесконечности равен 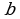 ; но обычно слова «при стремлении
; но обычно слова «при стремлении 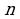 к бесконечности» отпускают).
к бесконечности» отпускают).
Дадим несколько пояснений.
Пусть 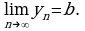 Возьмем интервал
Возьмем интервал 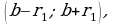 т.е. окрестность точки
т.е. окрестность точки 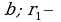 радиус этой окрестности
радиус этой окрестности  Существует номер
Существует номер 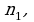 начиная с которого вся последовательность содержится в указанной окрестности:
начиная с которого вся последовательность содержится в указанной окрестности:  и т. д.
и т. д.
А что будет, если взять интервал 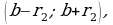 где
где 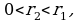 т.е. если уменьшить радиус окрестности? Опять найдется номер
т.е. если уменьшить радиус окрестности? Опять найдется номер 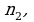 начиная с которого вся последовательность содержится в указанной окрестности, но этот номер больше, т.е.
начиная с которого вся последовательность содержится в указанной окрестности, но этот номер больше, т.е. 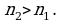
Свойства сходящихся последовательностей
Свойство 1. Если последовательность сходится, то только к одному пределу.
Свойство 2. Если последовательность сходится, то она ограничена.
Свойство 3. Если последовательность монотонна и ограниченна, то она сходится (теорема Вейерштрасса).
Вычисление пределов последовательностей
Выше мы отметили, что
 если
если 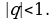
Добавим еще одно соотношение: 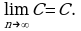
Иными словами, предел стационарной последовательности равен значению любого члена последовательности.
Для вычисления пределов последовательностей в более сложных случаях используются указанные соотношения и следующая теорема.
Теорема. Если 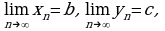 то
то
предел суммы равен сумме пределов:
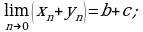
предел произведения равен произведению пределов:
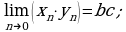
предел частного равен частному от пределов:
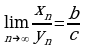
(но разумеется на дополнительных условиях: 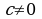 и
и 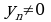 для любого
для любого 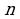 );
);
постоянный множитель можно вынести за знак предела:
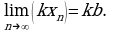
Пример 1. Найти пределы последовательностей:
а) 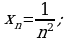 в)
в) 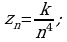
б) 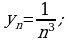 г)
г) 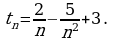
Решение. а) Имеем 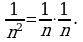 Применив правило «предел произведения», получим
Применив правило «предел произведения», получим
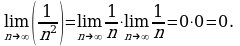
б) Рассуждая, как в п. а), получим 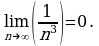
в) 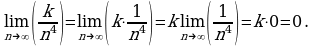
Вообще для любого показателя 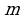 и для любого коэффициента
и для любого коэффициента 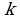 справедливо соотношение:
справедливо соотношение:
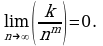
г) применив правило «предел суммы», получим
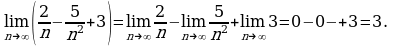
Пример 2. Даны числа 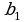 и
и 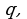 такие, что
такие, что 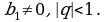 Вычислить
Вычислить 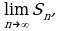 где
где 
Решение. Прежде всего воспользуемся тем, что постоянный множитель 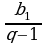 можно вынести за знак предела. Получим
можно вынести за знак предела. Получим
 Далее воспользуемся тем, что
Далее воспользуемся тем, что 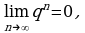 и, следовательно,
и, следовательно, 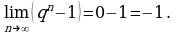 Тогда
Тогда
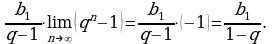
Пример 3. Вычислить 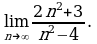
Решение. В подобных случаях применяют искусственный прием: делят числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной  В данном примере разделим числитель и знаменатель дроби почленно на
В данном примере разделим числитель и знаменатель дроби почленно на 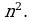 Получим
Получим
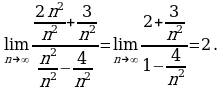
Сумма бесконечной геометрической прогрессии
Рассмотрим бесконечную геометрическую прогрессию
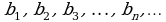
Будем последовательно вычислять суммы двух, трех, четырех и т.е. членов прогрессии: 
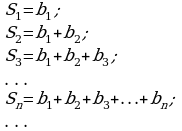
Получилась последовательность 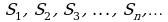 Как всякая числовая последовательность, она может сходится или расходится. Если последовательность
Как всякая числовая последовательность, она может сходится или расходится. Если последовательность 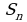 сходится к пределу
сходится к пределу  называют суммой геометрической прогрессии (обратите внимание: не суммой
называют суммой геометрической прогрессии (обратите внимание: не суммой 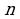 членов геометрической прогрессии, а суммой геометрической прогрессии). Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя о сумме
членов геометрической прогрессии, а суммой геометрической прогрессии). Если же эта последовательность расходится, то о сумме геометрической прогрессии не говорят, хотя о сумме 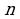 членов геометрической прогрессии можно, разумеется, говорить и в этом случае.
членов геометрической прогрессии можно, разумеется, говорить и в этом случае.
Напомним формулу суммы первых 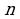 членов геометрической прогрессии:
членов геометрической прогрессии: 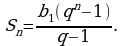 Рассмотрим случай, когда знаменатель
Рассмотрим случай, когда знаменатель 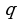 геометрической прогрессии удовлетворяет неравенству
геометрической прогрессии удовлетворяет неравенству 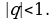
В примере 2 мы установили, что в этом случае 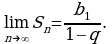 Но
Но 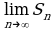 мы назвали выше суммой геометрической прогресси. Таким образом, мы доказали следующее утверждение.
мы назвали выше суммой геометрической прогресси. Таким образом, мы доказали следующее утверждение.
Если знаменатель 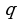 геометрической прогрессии
геометрической прогрессии  удовлетворяет неравенству
удовлетворяет неравенству  то сумма
то сумма  прогрессии вычисляется по формуле
прогрессии вычисляется по формуле 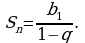
Пример 4. Найти сумму геометрической прогрессии 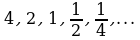
Решение. Здесь 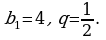 Поскольку знаменатель прогрессии удовлетворяет неравенству
Поскольку знаменатель прогрессии удовлетворяет неравенству  мы имеем право воспользоваться только что полученной формулой
мы имеем право воспользоваться только что полученной формулой 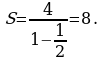
Степенные ряды
Степенным рядом называется ряд вида
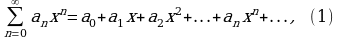
где числа  называется коэффициентами ряда, а член
называется коэффициентами ряда, а член 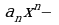 общим членом ряда.
общим членом ряда.
Областью сходимости степенного ряда называется множество всех значений 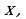 при которых данный ряд сходится.
при которых данный ряд сходится.
Число 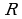 называется радиусом сходимости ряда (1), если при
называется радиусом сходимости ряда (1), если при 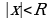 ряд сходится абсолютно, а при
ряд сходится абсолютно, а при 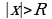 ряд расходится.
ряд расходится.
Радиус сходимости 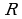 можно найти, используя признак Даламбера:
можно найти, используя признак Даламбера:
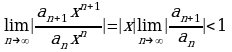 (
( не зависит от
не зависит от 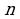 ), откуда
), откуда
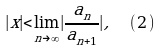
т.е. если ряд (1) сходится при любых 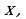 удовлетворяющих условию (2), и ряд сходится при
удовлетворяющих условию (2), и ряд сходится при
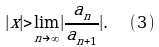
Отсюда следует, что если существует предел
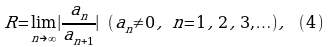
то радиус сходимости ряда 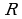 равен этому пределу и ряд (1) сходится при
равен этому пределу и ряд (1) сходится при  т.е. в промежутке
т.е. в промежутке 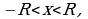 который называется промежутком (интервалом) сходимости.
который называется промежутком (интервалом) сходимости.
Если предел (4) равен нулю 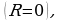 то ряд (1) сходится в единственной точке
то ряд (1) сходится в единственной точке 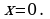
На концах промежутка ряд может сходится (абсолютно и условно), но может и расходиться. Сходимость ряда (1) при 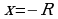 и
и  исследуется с помощью какого- либо из признака сходимости.
исследуется с помощью какого- либо из признака сходимости.
Пример 1. Дан ряд: 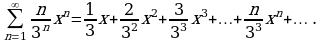
Исследовать его сходимость в точках 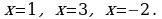
При 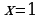 данный ряд превращается в числовой ряд
данный ряд превращается в числовой ряд
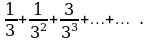
Исследуем сходимость этого ряда по признаку Даламбера. Имеем

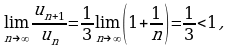 т.е. ряд сходится.
т.е. ряд сходится.
При 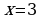 получим ряд
получим ряд
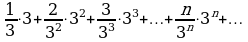
или
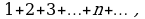 который расходится, так как не выполняется необходимый признак сходимости ряда
который расходится, так как не выполняется необходимый признак сходимости ряда 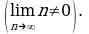
При  получим
получим
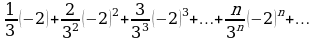
или
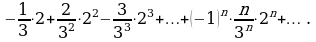
Это законочередующийся ряд, который, согласно признаку Лейбница, сходится.
Итак, в точках 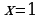 и
и  ряд сходится, а в точке
ряд сходится, а в точке 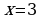 расходится.
расходится.
Пример 2. Найти промежуток сходимости степенного ряда:
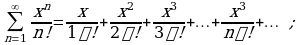
Используя формулу (4) получим:
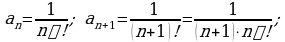
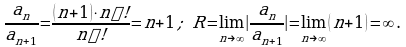
Следовательно, промежуток сходимости есть 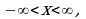 т.е. данный ряд сходится на всей числовой оси.
т.е. данный ряд сходится на всей числовой оси.
Пример 3. Найти промежуток сходимости степенного ряда:
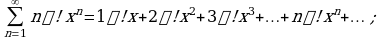
Согласно формуле (4), находим

Ряд сходится только в одной точке 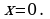
Пример 4. Найти промежуток сходимости степенного ряда:
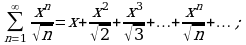
Используя формулу (4), получим
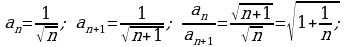
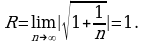
Следовательно, данный ряд сходится абсолютно при 
Исследуем сходимость ряда в точках 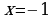 и
и 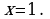 При
При 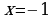 имеем ряд
имеем ряд
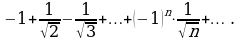
Это знакочередующийся ряд, который в силу признака Лейбница сходится.
При 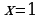 имеем ряд
имеем ряд

или
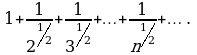
Это обобщенный гармонический ряд, который расходится, так как 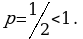 Отсюда следует, что данный ряд сходится при
Отсюда следует, что данный ряд сходится при 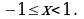
Разложение элементарных функций в ряд Маклорена.
Для приложений важно уметь данную функцию 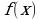 разлагать в степенной ряд, т.е. функцию
разлагать в степенной ряд, т.е. функцию 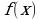 представлять в виде суммы степенного ряда.
представлять в виде суммы степенного ряда.
Рядом Тейлора для функции 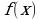 называется степенной ряд вида
называется степенной ряд вида
![]() .
.
Если 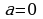 , то получим частный случай ряда Тейлора
, то получим частный случай ряда Тейлора
![]() ,
,
который называется рядом Маклорена.
Степенной ряд внутри его промежутка сходимости можно почленно дифференцировать и интегрировать сколько угодно раз, причем полученные ряды имеют тот же промежуток сходимости, что и исходный ряд.
Два степенных ряда можно почленно складывать и умножать по правилам сложения и умножения многочленов. При этом промежуток сходимости полученного нового ряда совпадает с общей частью промежутков сходимости исходных рядов.
Для разложения функции 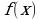 в ряд Маклорена необходимо:
в ряд Маклорена необходимо:
Вычислить значения функции и ее последовательных производных в точке 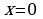 , т.е.
, т.е. 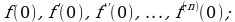
Составить ряд Маклорена, подставив значения функции и ее последовательных производных в формулу ряда Маклорена;
Найти промежуток сходимости полученного ряда по формуле
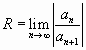 ,
, ![]() .
.
Таблица, содержащая разложения в ряд Маклорена некоторых элементных функций:
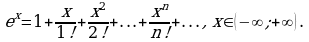
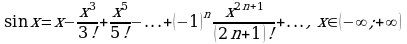 .
.

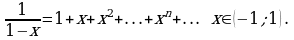
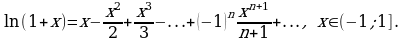
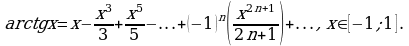
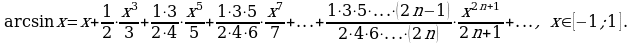
Пример 1. Разложить в ряд Маклорена функцию 
Решение. Так как  то, заменяя
то, заменяя  на
на 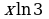 в разложении
в разложении 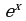 , получим:
, получим:
![]() ,
, ![]() .
.
Пример 2. Выписать ряд Маклорена функции 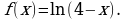
Решение. Так как 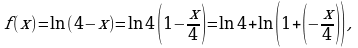 то воспользовавшись формулой (5), в которой заменим
то воспользовавшись формулой (5), в которой заменим  на
на 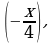 получим:
получим:
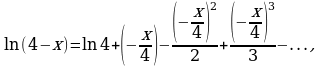
или

если 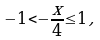 т.е.
т.е. 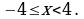
Пример 3. Разложить в ряд Маклорена функцию 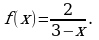
Решение. Воспользуемся формулой (4). Так как
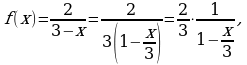 то заменив
то заменив  на
на 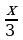 получим:
получим:
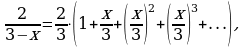
или 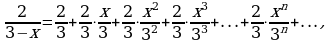
где 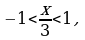 т.е.
т.е. 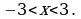
Задание 1. Исследовать по признаку Даламбера сходимость рядов:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Задание 2. Используя разложения в ряд Маклорена функции  разложить степенные ряды функции:
разложить степенные ряды функции:
а) 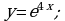 б)
б) 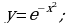 в)
в) 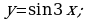 г)
г) 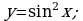 д)
д) 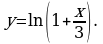
Множества.
План:
1. Множество, элемент множества.
2. Способы задания множеств.
3. Равенство множеств. Подмножество.
4. Бинарные отношения и их свойства.
5. Пересечение множеств.
6. Объединение множеств.
7. Разность множеств. Дополнение множества.
8. Алгебра множеств.
Множество, элемент множества. Понятию множество в математике не дается строгого определения. Создатель теории множеств немецкий математик Г. Кантор (1845-1918 гг.) писал: «Под… множеством я понимаю вообще всякое многое, которое можно мыслить, как единое».
Множества обозначаются буквами  Некоторые множества имеют специальные обозначения. Например,
Некоторые множества имеют специальные обозначения. Например,  множество натуральных чисел.
множество натуральных чисел.
Элементы множества в общем виде обозначаются  Запись
Запись  означает, что элемент
означает, что элемент 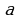 принадлежит множеству
принадлежит множеству 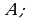 запись
запись 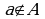 означает, что элемент
означает, что элемент 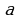 не принадлежит множеству
не принадлежит множеству 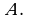 Рассматривают также пустое множество, т.е. множество не имеет ни одного элемента, обозначают Ø.
Рассматривают также пустое множество, т.е. множество не имеет ни одного элемента, обозначают Ø.
Способы задания множеств. Множество считается заданным, если относительно любого элемента можно сказать, принадлежит или не принадлежит этот элемент данному множеству.
Перечисление элементов. Например, множество  задано так:
задано так: 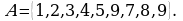 Ясно, что
Ясно, что 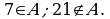 Заметим, что при таком способе задания множества не имеют значения порядок перечисления элементов.
Заметим, что при таком способе задания множества не имеют значения порядок перечисления элементов.
Указание характеристического свойства. Например, числовой промежуток 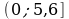 можно задать следующим образом:
можно задать следующим образом:
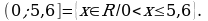 Здесь множество
Здесь множество  действительных чисел считается универсальным множеством; неравенство
действительных чисел считается универсальным множеством; неравенство 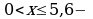 характеристическое свойство элементов данного множества.
характеристическое свойство элементов данного множества.
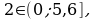 так как выполняется неравенство
так как выполняется неравенство 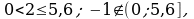 так как неравенство
так как неравенство  не выполняется. Легко заметить, что
не выполняется. Легко заметить, что 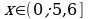 тогда и только тогда, когда выполняется неравенство
тогда и только тогда, когда выполняется неравенство 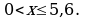
В общем виде запись множества, заданного с помощью характеристического свойства, выглядит следующим образом: 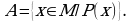 Здесь
Здесь 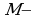 универсальное множество, высказывательная форма
универсальное множество, высказывательная форма 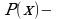 характеристическое свойство. При этом
характеристическое свойство. При этом
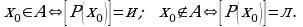
Таким образом, характеристическое свойство представляет собой необходимое и достаточное условие принадлежности элемента данному множеству.
Указание характеристического свойства- более универсальный способ задания множества, чем перечисление элементов. С помощью перечисления элементов можно задавать только так называемые конечные множества. Вместе с тем, существуют множества, например, 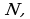 которое невозможно задать перечислением элементов. Такие множества называют бесконечными. С помощью характеристического свойства можно задавать как конечные, так и бесконечные множества.
которое невозможно задать перечислением элементов. Такие множества называют бесконечными. С помощью характеристического свойства можно задавать как конечные, так и бесконечные множества.
Равенство множеств. Подмножество.
Определение 1. Множества  и
и  называются равными, если они состоят из одних и тех же элементов.
называются равными, если они состоят из одних и тех же элементов.
Обозначение: 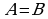 .
.
Например, равны множество  всех однозначных натуральных чисел и множество
всех однозначных натуральных чисел и множество  всех натуральных решений неравенства
всех натуральных решений неравенства 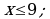 оба эти множества состоят из чисел
оба эти множества состоят из чисел 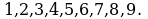 Также являются равными множества
Также являются равными множества 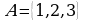 и
и 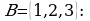 множество не изменяется при изменении порядка перечисления его элементов.
множество не изменяется при изменении порядка перечисления его элементов.
Определение 2. Множество  называется подмножеством множества
называется подмножеством множества 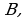 если любой элемент
если любой элемент  принадлежит
принадлежит 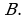
Обозначение: 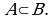 Символически:
Символически: 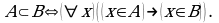
 Знак
Знак 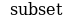 называют знаком включения. Запись
называют знаком включения. Запись  читают по-разному: «
читают по-разному: «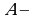 подмножество
подмножество  »; «
»; « включается в
включается в  », «
», « содержится в
содержится в  » и т. п.
» и т. п.
То, что 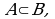 можно наглядно изобразить с помощью диаграммы Эйлера-Венна. На диаграмме Эйлера множество изображается, скажем, в виде круга, а элементы- множество- в виде точек этого круга.
можно наглядно изобразить с помощью диаграммы Эйлера-Венна. На диаграмме Эйлера множество изображается, скажем, в виде круга, а элементы- множество- в виде точек этого круга.
Бинарные отношения и их свойства.
Примеры и способы задания бинарных отношений. Элементы множеств, рассматриваемых в математике, могут находится в некоторых связях, или, иначе говоря, отношениях. Так, например, из двух действительных чисел одно может быть больше другого, одно натуральное число может делиться на другое; две прямые на плоскости могут быть параллельные или перпендикулярные.
Из всех видов возможных отношений наиболее важными являются бинарные отношения, то есть отношения, в которых могут находиться или не находиться любые два элемента одного множества.
Тот факт, что два элемента  и
и 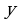 множества
множества  находятся между собой в некотором отношении, записывают часто так:
находятся между собой в некотором отношении, записывают часто так: 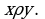 Читается: «элемент
Читается: «элемент  находится в бинарном отношении
находится в бинарном отношении 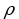 с элементом
с элементом 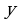 ». Здесь
». Здесь  символ бинарного отношения. То, что
символ бинарного отношения. То, что  и
и 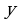 не находятся в отношении
не находятся в отношении 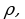 будем обозначать:
будем обозначать: 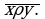
Для некоторых известных отношений употребляются специальные символы:  и другие. Бинарное отношение можно задать, перечислив все пары элементов, которые находятся в данном отношении. Сделать это возможно, если количество этих пар конечно, более того, не является очень большим. В случае бесконечного или очень большого числа соответствующих пар бинарное отношение задают характеристическим свойством.
и другие. Бинарное отношение можно задать, перечислив все пары элементов, которые находятся в данном отношении. Сделать это возможно, если количество этих пар конечно, более того, не является очень большим. В случае бесконечного или очень большого числа соответствующих пар бинарное отношение задают характеристическим свойством.
График любой числовой функции определяет бинарное отношение на множестве действительных чисел: число  находится в этом отношении с элементом
находится в этом отношении с элементом 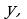 если точка
если точка 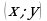 принадлежит графику данной функции. Фактически можно говорить еще об одном способе задания бинарных отношений: графическом.
принадлежит графику данной функции. Фактически можно говорить еще об одном способе задания бинарных отношений: графическом.
Еще один наглядный способ представлений бинарных отношений на конечных множествах- с помощью графов. Граф отношения строится следующим образом. Изобразим элементы множества, на котором задано бинарное отношение, точками плоскости и каждой паре 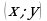 поставим в соответствие ребро, то есть линию со стрелкой, ведущей из точки
поставим в соответствие ребро, то есть линию со стрелкой, ведущей из точки  в точку
в точку 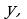 если элемент
если элемент  находится в отношении с
находится в отношении с 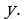 Если элемент
Если элемент  находится в отношении с
находится в отношении с 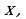 то проведем на плоскости петлю.
то проведем на плоскости петлю.
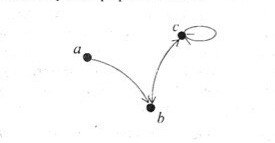 Таким образом, мы получим граф отношения:
Таким образом, мы получим граф отношения:
Обратим внимание на то, что о каком бы способе задания бинарного отношения мы не говорили, всегда шла речь о каком-то множестве упорядоченных пар, которое образует подмножество декартова произведения некоторых множеств. В соответствии с этими дается общее определение:
Пусть  и
и 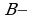 произвольные множества. Всякое подмножество
произвольные множества. Всякое подмножество  называется бинарным отношением между элементами множеств
называется бинарным отношением между элементами множеств  и
и 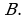
В частности, любое подмножество  называют бинарным отношением на множестве А.
называют бинарным отношением на множестве А.
Свойства бинарных отношений.
Рассмотрим свойства бинарных отношений, заданных на некотором множестве А.
Бинарное отношение 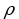 на множестве
на множестве 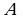 называется рефлексивным, если для каждого
называется рефлексивным, если для каждого  из
из  имеет место
имеет место 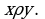 Символически:
Символически: 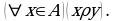
Примерами рефлексивных отношений являются отношения делимости на множестве целых чисел, равенства фигур, подобия треугольников, одинаковой направленности лучей в пространстве, включения множеств. Действительно, любое число делиться на себя, всякая фигура равна себе, любой треугольник подобен себе, любой луч имеет одинаковое направление с собой, всякое множество является подмножеством самого себя. Отношение «больше» на любом числовом множестве не является рефлексивным, так как утверждение, что любое число больше самого себя, является конечно ложным.
Бинарное отношение 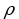 на множестве
на множестве 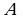 называется антирефлексивным, если для каждого
называется антирефлексивным, если для каждого  из
из 
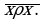 Символически:
Символически: 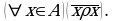
Примерами антирефлексивных отношений являются отношение «больше» и на множестве целых чисел, перпендикулярность прямых на плоскости, отношение неравенства чисел.
Бинарное отношение 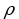 на множестве
на множестве 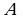 называется транзитивным, если для любых
называется транзитивным, если для любых 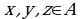 из того, что
из того, что 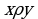 и
и 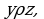 следует
следует  Символически
Символически 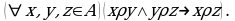
Примерами транзитивных отношений являются отношения параллельности прямых на плоскости, подобия фигур, равенство, отношение включения множеств, отношения на числовых множествах, делимость на множестве натуральных чисел и другие. Отношение 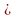 транзитивным не является. В самом деле, можно привести такие три прямые, что первая перпендикулярна второй и вторая перпендикулярна третьей, но первая не перпендикулярна третьей.
транзитивным не является. В самом деле, можно привести такие три прямые, что первая перпендикулярна второй и вторая перпендикулярна третьей, но первая не перпендикулярна третьей.
Бинарное отношение 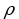 на множестве
на множестве  называется симметричным, если для любых
называется симметричным, если для любых 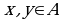 из того, что
из того, что  следует
следует  Символически:
Символически: 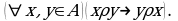
Примерами симметричных отношений являются отношения равенства, подобия, параллельности. Отношения  делимость целых чисел симметричными не являются.
делимость целых чисел симметричными не являются.
Бинарное отношение 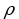 на множестве
на множестве 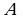 называется антисимметричным, если для любых
называется антисимметричным, если для любых 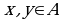 из того, что
из того, что 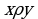 и
и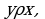 следует, что
следует, что 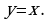 Символически:
Символически: 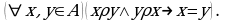 В контрапозиционной форме это может быть записано:
В контрапозиционной форме это может быть записано: 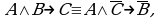 запишем эту формулировку в виде:
запишем эту формулировку в виде: 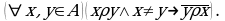
Примерами антисимметричных отношений является отношения 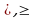 делимость на множестве натуральных чисел.
делимость на множестве натуральных чисел.
Бинарное отношение 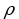 на множестве
на множестве 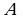 называется связным, если для любых неравных элементов
называется связным, если для любых неравных элементов 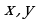 хотя бы один из элементов находится в данном отношении с другим. Символически это выглядит так:
хотя бы один из элементов находится в данном отношении с другим. Символически это выглядит так: 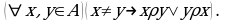
Примерами связных отношений являются отношения 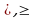 на числовых множествах. Отношения
на числовых множествах. Отношения  делимость на множестве натуральных чисел связными не являются.
делимость на множестве натуральных чисел связными не являются.
Операции над множествами.
Операции над множествами позволят из данных множеств получать новые множества.
Пересечение множеств.
Определение. Пересечение множеств  и
и  называется множество, состоящее из всех тех и только тех элементов, которые принадлежат обоим этим множествам.
называется множество, состоящее из всех тех и только тех элементов, которые принадлежат обоим этим множествам.
Обозначение: 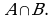
Иначе говоря, 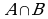 состоит из всех общих элементов множеств
состоит из всех общих элементов множеств  и B.
и B.
И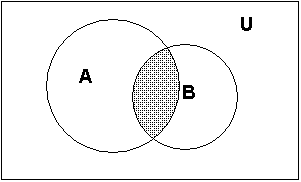 зобразим
зобразим 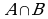 с помощью диаграммы Эйлера.
с помощью диаграммы Эйлера.
Здесь и в дальнейшем будем полагать, что множества  и B представляют собой подмножества некоторого множества
и B представляют собой подмножества некоторого множества 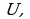 называемого универсальным множеством.
называемого универсальным множеством.
Множество 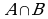 может быть задано с помощью характеристического свойства:
может быть задано с помощью характеристического свойства:
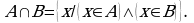
Таким образом: 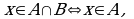 и
и 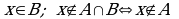 или
или 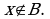
Заметим, что условие для 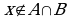 может быть получено из условия для
может быть получено из условия для  по закону де Моргана.
по закону де Моргана.
Пусть 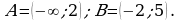 Тогда
Тогда 
Теорема 1. Множество истинности конъюнкции двух высказывательных форм равно пересечению множеств истинности этих высказывательных форм:
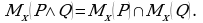
Объединение множеств.
Определение. Объединением множеств  и B называется множество, состоящее из всех тех только тех элементов, которые принадлежат хотя бы одному из этих множеств.
и B называется множество, состоящее из всех тех только тех элементов, которые принадлежат хотя бы одному из этих множеств.
Обозначение: 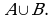
И зобразим
зобразим 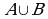 с помощью диаграммы Эйлера:
с помощью диаграммы Эйлера:
Зададим 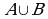 с помощью характеристического свойства:
с помощью характеристического свойства:
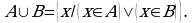
Имеем: 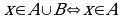 или
или 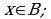
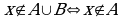 и
и 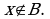
В условиях предыдущего примера, где 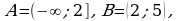 получим, что
получим, что 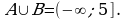
Теорема 2. Множество истинности дизъюнкции двух высказывательных форм равно объединению множеств истинности этих высказывательных форм:
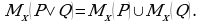
Разность множеств. Дополнение множества.
Определение. Разностью множества  и B называется множества, состоящее из всех тех и только тех элементов, которые принадлежат
и B называется множества, состоящее из всех тех и только тех элементов, которые принадлежат  и не принадлежат B.
и не принадлежат B.
Обозначение:  или
или  \
\
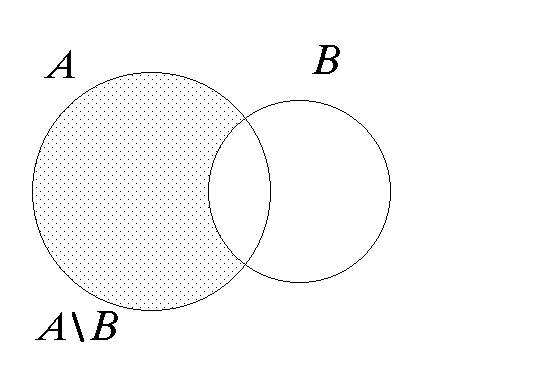 Изобразим диаграмму Эйлера для множеств
Изобразим диаграмму Эйлера для множеств 
С помощью характеристического свойства:
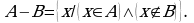
Отсюда: 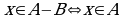 и
и 
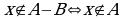 или
или 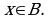
Если, как в предыдущих примерах, 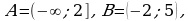 то получим, что
то получим, что 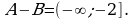
Разность универсального множества 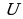 и множества
и множества  называют дополнением множества
называют дополнением множества  и обозначают
и обозначают 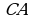 и
и 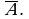
Имеем: 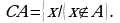 Тогда
Тогда 
Рассматривая тот же пример, где 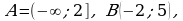 получим:
получим: 
Теорема 3. Множество истинности отрицания высказывательной формы равно дополнению множества истинности этой высказывательной формы:
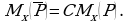
Алгебра множеств. Операции над множествами подчиняются законам, аналогичным законам логики*:
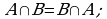
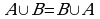 (коммуникативность).
(коммуникативность).
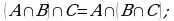
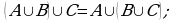
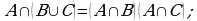
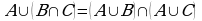 (дистрибутивность).
(дистрибутивность).
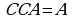 (закон двойного дополнения).
(закон двойного дополнения).

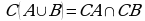 (законы де Моргана).
(законы де Моргана).
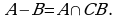
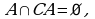
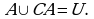
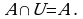


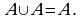
Все эти законы также доказываются «методом двух включений».
В качестве примера упростим сложное выражение, составленное из множеств:
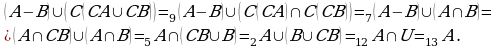
Говорят, что с помощью теоретико-множественных операций задается так называемая алгебра множеств. Преобразования, аналогичные приведенные выше- это преобразования выражений алгебры множеств.
Пример 1. Даны множества  и
и 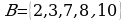
Найти: 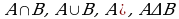 .
.
Решение: 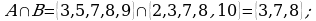

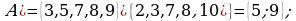
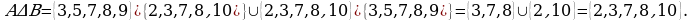
Пример 2. Даны множества 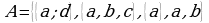 и
и 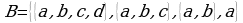
Найти: 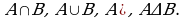
Решение:
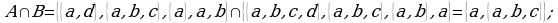
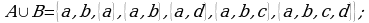
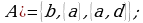

Пример 3. Даны промежутки 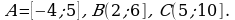 Найти следующие множества:
Найти следующие множества: 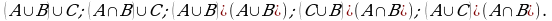
Пример 4. Выполните действия и определите мощность полученного множества: 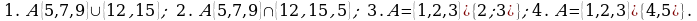
Пример 5. Из 35 студентов, побывавших на каникулах в Москве, все, кроме двоих, делились впечатлениями. О посещении Большого театра с восторгом вспоминали 12 человек, Кремля – 14, а 16 – о концерте, по три студента запомнили посещение театра и Кремля, а также театра и концерта, а четверо – концерта и пребывания в Кремле. Сколько студентов сохранили воспоминания одновременно о театре, концерте и Кремле?
Пример 6. Каждый студент группы программистов занимается в свободное время либо в НСО, либо спортом. Сколько студентов в группе, если 23 увлекаются спортом, 12 занимаются в НСО, а 7 совмещают занятия в НСО и увлечение спортом?
Тест № 1 (1 – вариант)
Тема: «Множества»
Вопрос № 1. Запись 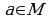 означает:
означает:
а) 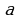 принадлежит множеству
принадлежит множеству 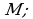
б) 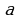 не принадлежит множеству
не принадлежит множеству 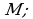
в) 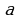 подмножество множества
подмножество множества 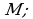
г) нет верного ответа.
Вопрос № 2. Множество считается заданным, если:
а) перечислены все его элементы;
б) указано свойство, которым обладают элементы, принадлежащие множеству;
в) нет верного ответа.
Вопрос № 3. Множество целых чисел принято обозначать:
а) N;
б) Z;
в) Q;
г) R.
Вопрос № 4. Множество принято изображать с помощью:
а) кругов Эйлера-Венна;
б) кругов Гаусса;
в) кругов Крамера;
г) нет верного ответа.
Вопрос № 5. Мощность множества – это:
а) число подмножеств данного множества;
б) число элементов данного множества;
в) число равных множеств данному множеству;
г) нет верного ответа.
Вопрос № 6. Множество, состоящее из тех и только тех элементов, которые принадлежат одновременно множествам  и
и  , называется:
, называется:
а) пересечением множеств  и
и  ;
;
б) объединением множеств  и
и  ;
;
в) разностью множеств  и
и  ;
;
г) нет верного ответа.
Вопрос № 7. Даны множества: 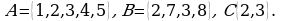
 - это:
- это:
а) пересечением множеств  и
и  ;
;
б) объединением множеств  и
и  ;
;
в) разностью множеств  и
и  ;
;
г) нет верного ответа.
Вопрос № 8. Пустым называется множество:
а) состоящее из нулевого элемента;
б) не содержащее элементов;
в) содержащее один элемент;
г) нет верного ответа.
Тест № 1 (2 - вариант)
Тема: «Множества»
Вопрос № 1. Запись 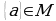 означает:
означает:
а) 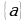 принадлежит множеству
принадлежит множеству 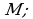
б) 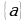 не принадлежит множеству
не принадлежит множеству 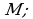
в)  подмножество множества
подмножество множества 
г) нет верного ответа.
Вопрос № 2. Множество считается заданным, если:
а) перечислены все его элементы;
б) указано свойство, которым обладают элементы, принадлежащие множеству;
в) нет верного ответа.
Вопрос № 3. Множество натуральных чисел принято обозначать:
а) N;
б) Z;
в) Q;
г) R.
Вопрос № 4. Множество принято изображать с помощью:
а) кругов Эйлера-Венна;
б) кругов Гаусса;
в) кругов Крамера;
г) нет верного ответа.
Вопрос № 5. Мощность множества – это:
а) число подмножеств данного множества;
б) число элементов данного множества;
в) число равных множеств данному множеству;
г) нет верного ответа.
Вопрос № 6. Множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств  и
и  , называется:
, называется:
а) пересечением множеств  и
и  ;
;
б) объединением множеств  и
и  ;
;
в) разностью множеств  и
и  ;
;
г) нет верного ответа.
Вопрос № 7. Даны множества: 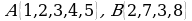 и
и 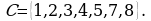
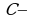 это:
это:
а) пересечением множеств  и
и  ;
;
б) объединением множеств  и
и  ;
;
в) разностью множеств  и
и  ;
;
г) нет верного ответа.
Вопрос № 8. Пустым называется множество:
а) состоящее из нулевого элемента;
б) не содержащее элементов;
в) содержащее один элемент;
г) нет верного ответа.
Тест № 1 (3 – вариант)
Тема: «Множества»
Вопрос № 1. Запись 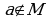 означает:
означает:
а) 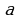 принадлежит множеству
принадлежит множеству 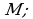
б) 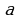 не принадлежит множеству
не принадлежит множеству 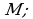
в) 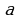 подмножество множества
подмножество множества 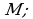
г) нет верного ответа.
Вопрос № 2. Множество считается заданным, если:
а) перечислены все его элементы;
б) указано свойство, которым обладают элементы, принадлежащие множеству;
в) нет верного ответа.
Вопрос № 3. Множество рациональных чисел принято обозначать:
а) N;
б) Z;
в) Q;
г) R.
Вопрос № 4. Множество принято изображать с помощью:
а) кругов Эйлера-Венна;
б) кругов Гаусса;
в) кругов Крамера;
г) нет верного ответа.
Вопрос № 5. Мощность множества – это:
а) число подмножеств данного множества;
б) число элементов данного множества;
в) число равных множеств данному множеству;
г) нет верного ответа.
Вопрос № 6. Множество, состоящее из тех и только тех элементов множества 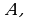 которые не принадлежат множеству
которые не принадлежат множеству 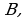 называется:
называется:
а) пересечением множеств  и
и 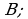
б) объединением множеств  и
и 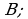
в) разностью множеств  и
и 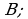
г) нет верного ответа.
Вопрос № 7. Даны множества: 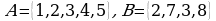 и
и 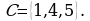
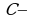 это:
это:
а) пересечением множеств  и
и 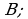
б) объединением множеств  и
и 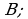
в) разностью множеств  и
и 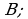
г) нет верного ответа.
Вопрос № 8. Пустым называется множество:
а) состоящее из нулевого элемента;
б) не содержащее элементов;
в) содержащее один элемент;
г) нет верного ответа.
Элементы математической логики
План:
Высказывания и высказывательные формы.
Логические операции.
Равносильность формул.
Высказывания и высказывательные формы.
Вычказывания и высказывательные формы. В математике основными являются два типа предложений: высказывания и высказывательные формы.
Высказывание- это повествовательное предложение, о котором можно сказать что оно истинно или ложно.
Например, предложение «Все натуральные числа положительны»- истинное высказывание; предложение «Река Обь впадает в Каспийское море»- ложное высказывание.
Предполагается, что высказывания подчиняются двум законам:
Закон противоречия. Никакое высказывание не может быть одновременно быть истинным или ложным.
Закон исключенного третьего. Всякое высказывание либо истинно, либо ложно («третьего не дано»).
Высказывания принято обозначать буквами:  Если высказывание
Если высказывание  истинно, то будем записывать:
истинно, то будем записывать: 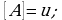 если высказывание
если высказывание  ложно, то запишем:
ложно, то запишем: 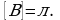
Например, [sin- нечетная функция]=и; 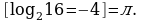
Верные числовые равенства и неравенства- это истинные высказывания; неверные числовые высказывания- это ложные высказывания;
Примером выказывательной формы может служить предложение «x- четное число». Оно не является высказыванием, так как о нем ничего нельзя сказать, истинно оно или ложно. Истинность этого предложения зависит от значения переменной х. Если вместо х подставить, например, натуральное число 4, то получим истинное высказывание; если же переменной х придать значение, равное 27, то получим ложное высказывание.
Высказывательной формой (или предикатом) называют предложение с переменными, которое становиться высказыванием, если вместо переменных подставить их значения из некоторого множества.
Примерами высказывательных форм являются уравнения и неравенства с переменными.
В зависимости от числа переменных различают одноместные, двуместные и т.д. формы. Обозначения: 
Например, пусть  обозначают высказывательную форму
обозначают высказывательную форму 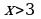 на множестве N. Тогда P(1)- высказывание
на множестве N. Тогда P(1)- высказывание 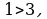 т.е.
т.е. 
Уравнение 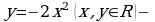 двуместная высказывательная форма. Обозначим ее
двуместная высказывательная форма. Обозначим ее 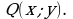 В этом случае
В этом случае 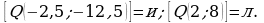
Логические операции
Конъюнкция (от латинского conjunctio- «соединение»). Эта логическая операция соответствует союзу «и». Рассмотрим пример: «cos- функция периодическая и четная». Данное сложное высказывание состоит из двух: «cos- функция периодическая», «cos- функция четная». Оба этих простых высказывания истины, поэтому и сложное высказывание «cos- функция периодическая и четная» является истинным. В высказывании «sin- функция периодическая и четная» второе простое высказывание ложно, все сложное высказывание также ложно.
Определение 1. Конъюнкцией высказываний A, B называется сложное высказывание, истинное тогда и только тогда, когда истинны оба высказывания А, B.
Обозначение: 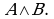
Из определения следует, что конъюнкция двух высказываний ложна тогда и только тогда, когда ложно хотя бы одно из высказываний.
По- другому конъюнкцию можно задать с помощью так называемой таблицы истинности, которая показывает зависимость значения истинности сложного высказывания от значений входящих в него простых высказываний:
| A | B |
|
| и | и | и |
| и | л | л |
| л | и | л |
| л | л | л |
Дизъюнкция (от латинского disjunction- «разделение»). Пусть, например, требуется нарисовать равнобедренный или прямоугольный треугольник. Для того, чтобы правильно выполнить задание, можно нарисовать один из трех видов треугольников: равнобедренный не прямоугольный, прямоугольный не равнобедренный, равнобедренный прямоугольный.
Такому пониманию союза «или» соответствует следующее
Определение 2. Дизъюнкция высказываний А, В называется сложное высказывание, истинное тогда и только тогда, когда истинно хотя бы одно из высказываний А, В.
Обозначение: 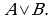
Дизъюнкция двух высказываний ложна тогда и только тогда, когда ложны оба эти высказывания.
Зададим дизъюнкцию с помощью таблицы истинности:
| А | B |
|
| и | и | и |
| и | л | и |
| л | и | и |
| л | л | л |
Пример дизъюнкции- числовое 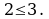 Логическая структура этого неравенства имеет вид:
Логическая структура этого неравенства имеет вид: 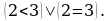 Данное высказывание истинно, так как верно неравенство 2
Данное высказывание истинно, так как верно неравенство 2
Заметим, что логические операции конъюнкция и дизъюнкция позволяют связывать любое число высказываний. При этом их конъюнкция истинна тогда и только тогда, когда истинны все составляющие ее высказывания, а дизъюнкция истинна тогда и только тогда, когда истинное хотя бы одно из них.
Импликация (от латинского implicite- «тесно связываю»). Логическая операция «импликация» соответствует союзу «если…, то». Перед тем как вести определение этой важнейшей для математики операции, рассмотрим следующую ситуацию. Предположим, что отец сказал сыну: «Если я получу премию, то куплю тебе велосипед». Обозначим через А высказывание «я получу премию», а через B- «я куплю велосипед». Тогда обещание отца запишем так: 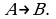 Если отец выполнит обещание, то высказывание
Если отец выполнит обещание, то высказывание 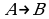 естественно считать истинным, а если нет- ложным. Рассмотрим все возможные случаи.
естественно считать истинным, а если нет- ложным. Рассмотрим все возможные случаи.
Отец получил премию и купил сыну велосипед. Все высказывания 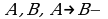 истинные.
истинные.
Отец премию получил премию, но велосипед не купил. Здесь  истинно, B ложно.
истинно, B ложно. 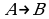 ложно, так как отец не выполнил обещание.
ложно, так как отец не выполнил обещание.
Отец не получил премию, но велосипед купил. В этом случае А ложно, В истинно, 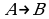 истинно, так как поступок отца не является нарушение обещания.
истинно, так как поступок отца не является нарушение обещания.
Отец не получил премию и велосипед не купил. Здесь А, В ложны. 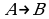 нельзя считать ложным, так как отец и в этом случае не нарушил обещания.
нельзя считать ложным, так как отец и в этом случае не нарушил обещания.
Это показывает целесообразность следующего определения.
Определение 3. Импликация высказываний А, В называется сложное высказывание, ложное тогда и только тогда, когда A истинное, а В ложно.
Импликация 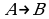 читается «если А, то В», «А импликация В». В этой импликации А называют условием, В- заключением.
читается «если А, то В», «А импликация В». В этой импликации А называют условием, В- заключением.
Приведем таблицу истинности для импликации:
| А | В |
|
| и | и | и |
| и | л | л |
| л | и | и |
| л | л | и |
Отрицание. Эта логическая операция в отличии от предыдущих производится не над двумя, а над одним высказыванием. Действие этой операции соответствует действию частицы «не» в естественном языке. Например, отрицанием высказывания «число 47 делится на 7» является высказывание «47 не делится на 7».
Определение 4. Отрицание высказывания А называется такое высказывание, которое истинно тогда и только тогда, когда А ложно.
Обозначения: 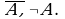
Таблица истинности:
| А |
|
| и | л |
| л | и |
Таким образом, нами введены логические операции конъюнкция, дизъюнкция, импликация, отрицание. Знаки этих операций  называют логическими связками.
называют логическими связками.
Равносильность формул. Введем следующее важно понятие.
Определение 5. Две формулы с одними и теми же высказывательными переменными называются равносильными, если они принимают одинаковые истинностные значения в каждой строке таблицы истинности.
Обозначение: 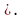 Например,
Например, 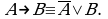
Законы логики. Наши рассуждения подчиняются определенным правилам, которые называются законами логики. Запишем некоторые из них в виде равносильностей логических формул.
1. 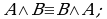
2. 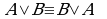 (коммутативность).
(коммутативность).
3. 
4. 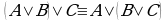 (ассоциативность).
(ассоциативность).
5. 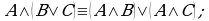
6. 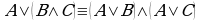 (дистрибутивность).
(дистрибутивность).
7. 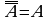 (закон двойного отрицания).
(закон двойного отрицания).
8. 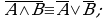
9. 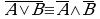 (законы де Моргана);
(законы де Моргана);
10. 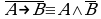 (закон отрицания импликации).
(закон отрицания импликации).
11. 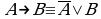 (закон устранения импликации).
(закон устранения импликации).
12. 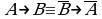 (закон контрапозиции).
(закон контрапозиции).
13. 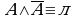 (противоречия);
(противоречия);
14. 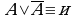 (исключенного третьего).
(исключенного третьего).
Случайное событие и его вероятность.
План:
Случайность события.
Классическое определение вероятности
Теорема сложения вероятностей.
Теоремы умножения вероятностей.
Основные понятия.
Математическое ожидание.
Дисперсия случайной величины
Среднеквадратическое отклонение
Случайность события.
Изучение каждого явления в порядке наблюдения опыта связано с осуществлением некоторого комплекса условий (испытаний). Всякий результат и исход испытания называется событием.
Если событие при заданных условиях может произойти или не произойти, то оно называется случайным. В том числе, когда событие должно непременно произойти, его называют достоверным, а в том случае, когда оно заведомо не может произойти, - невозможным.
События называются несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из событий не исключает появление другого при этом же испытании.
События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны.
Вероятность события рассматривается как мера объективной возможности появления случайного события.
Классическое определение вероятности. Вероятностью события  называется отношение числа исходов
называется отношение числа исходов  благоприятствующих наступлению данного события
благоприятствующих наступлению данного события  , к числу
, к числу 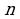 всех исходов (несовместных, единственно возможных и равновозможных), т.е.
всех исходов (несовместных, единственно возможных и равновозможных), т.е.
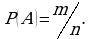 (1)
(1)
Вероятность любого события не может быть меньше нуля и больше единицы, т.е. 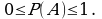 Невозможному событию соответствует вероятность
Невозможному событию соответствует вероятность 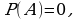 а достоверному- вероятность
а достоверному- вероятность 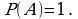
Пример 1. В лотерее из 1000 билетов имеются 200 выигрышных. Вынимают наугад один билет. Чему равна вероятность того, что этот билет выигрышный?
Решение. Общее число различных исходов есть  Число исходов, благоприятствующих получению выигрыша, составляет
Число исходов, благоприятствующих получению выигрыша, составляет 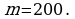 Согласно формуле (1), получим
Согласно формуле (1), получим 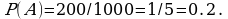
Пример 2. Из урны, в которой находятся 6 белых и 3 черных шара, вынимают один шар. Найти вероятность того, что шар окажется черным.
Решение. Обозначим событие, состоящее в появлении черного шара, через  . Общее число случаев
. Общее число случаев 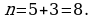 Число случаев
Число случаев 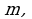 благоприятствующих появлению события
благоприятствующих появлению события  , равно 3. По формуле (1) получим
, равно 3. По формуле (1) получим 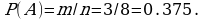
Пример 3. Из урны, в которой находятся 12 белых и 8 черных шаров, вынимают наудачу два шара. Какова вероятность того, что оба шара окажутся черными?
Решение. Обозначим событие, состоящее в появлении двух черных шаров, через  . Общее число возможных случаев
. Общее число возможных случаев 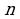 равно числу сочетаний 20 элементов (12+8) по два:
равно числу сочетаний 20 элементов (12+8) по два:
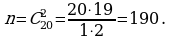
Число случаев 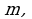 благоприятствующих событию
благоприятствующих событию  , составляет
, составляет

По формуле (1) находим вероятность появления двух черных шаров:

Пример 4. В партии из 18 деталей находятся 4 бракованных. Наугад выбирают 5 деталей. Найти вероятность того, что из этих 5 деталей две окажутся бракованными.
Решение. Число всех возможных независимых исходов 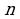 равно числу сочетаний 18 по 5, т.е.
равно числу сочетаний 18 по 5, т.е.

Подсчитаем число исходов 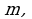 благоприятствующих событию
благоприятствующих событию  . Среди 5 взятых деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
. Среди 5 взятых деталей должно быть 3 качественных и 2 бракованных. Число способов выборки двух бракованных деталей из 4 имеющихся бракованных равно числу сочетаний из 4 по 2:
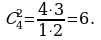
Число способов выборки трех качественных деталей из 14 имеющихся качественных равно
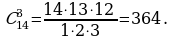
Любая группа качественных деталей может комбинироваться с любой группой бракованных деталей, поэтому общее число комбинаций  благоприятствующих этому событию, к числу
благоприятствующих этому событию, к числу  всех равновозможных независимых исходов:
всех равновозможных независимых исходов:
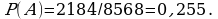
Задачи:
В ящике с деталями оказалось 300 деталей I сорта, 200 деталей II сорта и 50 деталей III сорта. Наудачу вынимают одну из деталей. Чему равна вероятность вынуть деталь I, II или III сорта?
В урне находятся 20 белых и 16 черных шаров. Наудачу вынимают один шар, который оказался белым, и откладывают его в сторону. После этого будет еще один шар. Найдите вероятность того, что этот шар также окажется белым.
В урне находится 7 белых и 5 черных шаров. Найдите вероятность того, что: 1) наудачу вынутый шар окажется черным; 2) два наудачу вынутых шара окажутся черными.
Считая выпадение любой грани игральной кости одинаково вероятным, найдите вероятность выпадения грани с нечетным числом очков.
В коробке имеются 30 лотерейных билетов, из которых 26 пустых (без выигрышей). Наугад вынимают одновременно 4 билета. Найдите вероятность того, что из 4 билетов два окажутся выигрышными.
Теоремы сложения и умножение вероятностей.
Теорема сложения вероятностей
Теорема сложения вероятностей несовместных событий. Вероятность появления одного из нескольких попарно несовместимых событий, безразлично какого, равна сумме вероятностей этих событий:
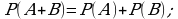 (2)
(2)
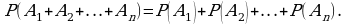 (3)
(3)
Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
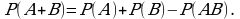 (4)
(4)
Для трех совместных событий имеет место формула
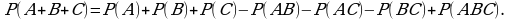 (5)
(5)
Событие, противоположное событию A (т.е. ненаступление A), обозначают  Сумма вероятностей двух противоположных событий равна единице:
Сумма вероятностей двух противоположных событий равна единице:
 (6)
(6)
Вероятность наступления события А, вычисленная в предположении, что событие B уже произошло, называется условной вероятностью события А при условии B и обозначается 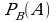 или
или 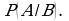
Если A и B- независимые события, то
 (7)
(7)
События А, В, С, … называется независимые в совокупности, если вероятность каждого из них не меняется в связи с наступлением или ненаступление других событий по отдельности или в любой их комбинации.
Пример 1. В ящике в случайном порядке разложены 20 деталей, причем пять из них стандартные. Рабочий берет наудачу три детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется стандартной (событие А).
Решение 1 способ. Очевидно, что по крайней мере одна из взятых деталей окажется стандартной, если произойдет любое из трех несовместимых событий: В- одна деталь стандартная, две нестандартные; С- две детали стандартные, одна нестандартная и D- три детали стандартные.
Таким образом, событие А можно представить в виде суммы этих трех событий:  По теореме сложения имеем
По теореме сложения имеем 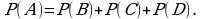 Находим вероятность каждого из этих событий:
Находим вероятность каждого из этих событий:

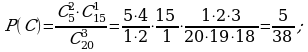
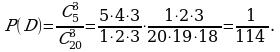
Сложив найденные величины, получим 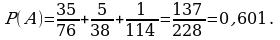
2 способ. События А (хотя бы одна из трех взятых деталей оказалась стандартной) и  (ни одна из взятых деталей не оказалась стандартной) являются противоположными; поэтому
(ни одна из взятых деталей не оказалась стандартной) являются противоположными; поэтому  или
или 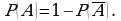
Вероятность появления события 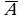 составляет
составляет
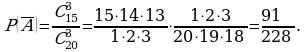
Следовательно, искомая вероятность есть  .
.
Пример 2. Найти вероятность того, что наудачу взятое двузначное число окажется либо кратным 3, либо 5, либо тому и другому одновременно.
Решение. Пусть А- событие, состоящее в том, что наудачу взятое число кратно 3, а В- в том, что оно кратно 5. Найдем 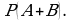 Так как A и B совместные события, то воспользуемся формулой (4):
Так как A и B совместные события, то воспользуемся формулой (4):
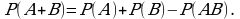
Всего имеется 90 двузначных чисел: 10, 11, …,98, 99. Из них 30 являются кратными 3 (благоприятствуют наступлению события А); 18- кратным 5 (благоприятствует наступления события В) и 6- кратным одновременно 3 и 5 (благоприятствуют наступлению события АВ). Таким образом, 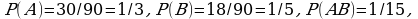 т.е.
т.е.
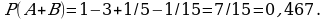
Задачи:
В ящике в случайном порядке положены 10 деталей, из которых 4 стандартных. Контролер взял наудачу 3 детали. Найдите вероятность того, что, хотя бы одна из взятых деталей оказалась стандартной.
В урне находится 10 белых, 15 черных, 20 синих и 25 красных аров. Найдите вероятность того, что вынутый шар окажется: 1) белым; 2) черным или красным.
Найдите вероятность того, что наудачу взятое двузначное число окажется кратным либо 4, либо 5, либо тому и другому одновременно.
Теоремы умножения вероятностей.
Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
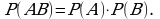 (8)
(8)
Вероятность появления нескольких событий, независимых в совокупности, вычисляется по формуле
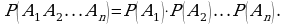 (9)
(9)
Теорема умножения вероятностей независимых событий. Вероятность совместного появления двух зависимых событий равна произведению одного из них на условную вероятность второго:
 (10)
(10)
Пример 3. В одной урне находятся 4 белых и 8 черных шаров, в другой- 3 белых и 9 черных. Из каждой урны вынули по шару. Найти вероятность того, что оба шара окажутся белыми.
Решение. Пусть А- появление белого шара из первой урны, а В- появление белого шара из второй урны. Очевидно, что события А и В независимы. Найдем 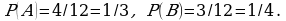 По формуле (8) получим
По формуле (8) получим
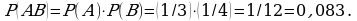
Пример 4. В ящике находится 12 деталей из которых 8 стандартных. Рабочий берет наудачу одну за другой две детали. Найти вероятность того, что обе детали окажутся стандартными.
Решение. Введем следующие обозначения: А- первая взятая деталь стандартная; В- вторая взятая деталь стандартная. Вероятность того, что первая деталь стандартная, составляет  Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартная первая деталь, т.е. условная вероятность события В, равна
Вероятность того, что вторая взятая деталь окажется стандартной при условии, что была стандартная первая деталь, т.е. условная вероятность события В, равна 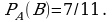
Вероятность того, что обе детали окажутся стандартными, находим по теореме умножения вероятностей зависимых событий:
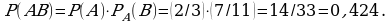
Задачи:
Рабочий обслуживает два автомата, работающих независимо друг от друга. Вероятность того, что в течении часа первый автомат не потребует внимания рабочего, равна 0,8, а для второго автомата эта вероятность 0,7. Найдите вероятность того, что в течении часа ни один из автоматов не потребует внимания рабочего.
В урне находится 6 шаров, из которых 3 белых. Наудачу вынуты один за другим два шара. Вычислите вероятность того, что оба шара окажутся белыми.
В урне находятся 10 белых и 6 черных шаров. Найдите вероятность того, что три наудачу вынутых один за другим шара окажутся черными.
Случайная величина.
Случайной называют величину, которая в результате испытания примет одно и только одно числовое значение, зависящее от случайных факторов и заранее непредсказуемое.
Случайные величины, как правило, обозначают через , а их значения – соответствующими маленькими буквами с подстрочными индексами, например,
, а их значения – соответствующими маленькими буквами с подстрочными индексами, например, .
.
Пример: X– количество очков, которое выпадет после броска игрального кубика.
В результате данного испытания выпадет одна и только грань, какая именно – не предсказать (фокусы не рассматриваем); при этом случайная величина X может принять одно из следующий значений: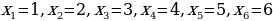 .
.
Пример из статистической вероятности:Y – количество мальчиков среди 10 новорождённых.
Совершенно понятно, что это количество заранее не известно, и в очередном десятке родившихся детей может оказаться: , мальчиков – один и только один из перечисленных вариантов.
, мальчиков – один и только один из перечисленных вариантов.
И, дабы соблюсти форму, немного физкультуры: Z– дальность прыжка в длину (в некоторых единицах). Её не в состоянии предугадать даже мастер спорта :)
Тем не менее, ваши гипотезы?
Коль скоро, множество действительных чисел бесконечно, то случайная величина Z может принять бесконечно много значений из некоторого промежутка. И в этом состоит её принципиальное отличие от предыдущих примеров.
Таким образом, случайные величины целесообразно разделить на 2 большие группы:
1) Дискретная (прерывная) случайная величина – принимает отдельно взятые, изолированные значения. Количество этих значений конечно либо бесконечно, но счётно.
2) Непрерывная случайная величина – принимает все числовые значения из некоторого конечного или бесконечного промежутка.
Примечание: в учебной литературе популярны аббревиатуры ДСВ и НСВ
Разберём дискретную случайную величину.
Закон распределения дискретной случайной величины
– это соответствие между возможными значениями этой величины и их вероятностями. Чаще всего закон записывают таблицей:
| X | x1 | x2 | x3 | … | xn |
| p1 | p2 | p3 | … | pn |
А теперь очень важный момент: поскольку случайная величина X обязательно примет одно из значений  , то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:
, то соответствующие события образуют полную группу и сумма вероятностей их наступления равна единице:  .
.
Так, например, закон распределения вероятностей выпавших на кубике очков имеет следующий вид:
| X | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
|
Возможно, у вас сложилось впечатление, что дискретная случайная величина может принимать только «хорошие» целые значения. Развеем иллюзию – они могут быть любыми:
Пример 1
Некоторая игра имеет следующий закон распределения выигрыша:
| U | -5 | 2,5 | 10 |
|
|
| 0,1 |
Найти 
Решение: так как случайная величина U может принять только одно из трёх значений, то соответствующие события образуют полную группу, а значит, сумма их вероятностей равна единице:  . Получаем: 0,5
. Получаем: 0,5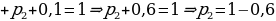 – таким образом, вероятность выигрыша
– таким образом, вероятность выигрыша 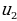 условных единиц составляет 0,4.
условных единиц составляет 0,4.
Контроль: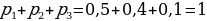 , в чём и требовалось убедиться.
, в чём и требовалось убедиться.
Ответ: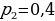
Не редкость, когда закон распределения требуется составить самостоятельно. Для этого используют классическое определение вероятности, теоремы умножения / сложения вероятностей событий:
Пример 2
В коробке находятся 50 лотерейных билетов, среди которых 12 выигрышных, причём 2 из них выигрывают по 1000 рублей, а остальные – по 100 рублей. Составить закон распределения случайной величины V – размера выигрыша, если из коробки наугад извлекается один билет.
Решение: как вы заметили, значения случайной величины принято располагать в порядке их возрастания. Поэтому мы начинаем с самого маленького выигрыша, и именно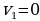 рублей.
рублей.
Всего таковых билетов 50 – 12 = 38, и по классическому определению: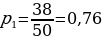 – вероятность того, что наудачу извлечённый билет окажется без выигрышным. С остальными случаями всё просто. Вероятность выигрыша
– вероятность того, что наудачу извлечённый билет окажется без выигрышным. С остальными случаями всё просто. Вероятность выигрыша 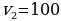 рублей составляет:
рублей составляет: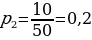 . И для
. И для 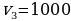 :
: . Проверка:
. Проверка: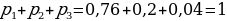 .
.
Ответ: искомый закон распределения выигрыша:
| V | 0 | 100 | 1000 |
|
| 0,2 | 0,04 |
Следующее задание для самостоятельного решения:
Пример 3
Вероятность того, что стрелок поразит мишень, равна p=0,7. Составить закон распределения случайной величины W – количества попаданий после 2 выстрелов.
Закон распределения полностью описывает случайную величину, однако на практике бывает полезно знать лишь некоторые её числовые характеристики: математическое ожидание, дисперсия, среднеквадратическое отклонение.
Математическое ожидание дискретной случайной величины
Говоря простым языком, это средне ожидаемое значение при многократном повторении испытаний. Пусть случайная величина X принимает значения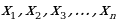 с вероятностями
с вероятностями 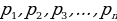 соответственно. Тогда математическое ожидание M(X) данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности:
соответственно. Тогда математическое ожидание M(X) данной случайной величины равно сумме произведений всех её значений на соответствующие вероятности: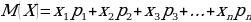 .
.
Вычислим, например, математическое ожидание случайной величины X – количества выпавших на игральном кубике очков: 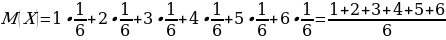 =
=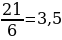 очка.
очка.
В чём состоит вероятностный смысл полученного результата? Если подбросить кубик достаточно много раз, то среднее значение выпавших очков будет близко к 3,5 – и чем больше провести испытаний, тем ближе.
Творческое задание для самостоятельного исследования:
Пример 4
Мистер Х играет в европейскую рулетку по следующей системе: постоянно ставит 100 рублей на «красное». Составить закон распределения случайной величины X – его выигрыша. Вычислить математическое ожидание выигрыша и округлить его до копеек. Сколько в среднем проигрывает игрок с каждой поставленной сотни?
Справка: европейская рулетка содержит 18 красных, 18 чёрных и 1 зелёный сектор («зеро»). В случае выпадения «красного» игроку выплачивается удвоенная ставка, в противном случае она уходит в доход казино
Пример 5
Случайная величина X задана своим законом распределения вероятностей:
| X | -1 | 0 | x3 | 5 |
|
| 0,2 | 0,1 | 0,4 |
Найти x3, если известно, что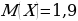 . Выполнить проверку.
. Выполнить проверку.
Дисперсия
Представим двух стрелков, которые стреляют по мишени. Один стреляет метко и попадает близко к центру, а другой… просто развлекается и даже не целится. Но что забавно, его средний результат будет точно таким же, как и у первого стрелка! Эту ситуацию условно иллюстрируют следующие случайные величины:
| X | -1 | 1 |
| 0,5 | 0,5 |
| Y | -100 | 100 |
| 0,5 | 0,5 |
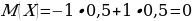 , однако и у «интересной личности»:
, однако и у «интересной личности»: 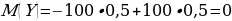 – оно тоже нулевое!
– оно тоже нулевое! Таким образом, возникает потребность количественно оценить, насколько далеко рассеяны пули (значения случайной величины) относительно центра мишени (математического ожидания). Ну а рассеяние с латыни переводится не иначе, как дисперсия.
Дисперсия случайной величины — мера разброса значений случайной величины относительно её математического ожидания. Формула для нахождения дисперсии 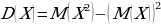
Пример: Вычислим дисперсию для следующей ДСВ заданной следующим законом распределения:
| X | -5 | 2,5 | 10 |
| 0,5 | 0,4 | 0,1 |
Вычислим сначала математическое ожидание: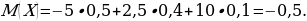 Теперь найдём математическое ожидание
Теперь найдём математическое ожидание  ) – квадрата случайной величины X. По определению математического ожидания:
) – квадрата случайной величины X. По определению математического ожидания: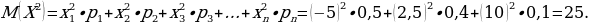 Таким образом, по формуле:
Таким образом, по формуле:
Еще одна числовая характеристика ДСВ – это среднеквадратическое отклонение.
Среднеквадратическое отклонение используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины: .
.
Пример: Дискретная случайная величина задана своим законом распределения:
| X | -2 | 0 | 3 | 7 |
| 0,4 | 0,1 | 0,3 | 0,2 |
Найти её математическое ожидание, дисперсию и среднеквадратическое отклонение. Эта задача встречается повсеместно, и, как правило, идёт без содержательного смысла.
Решение: Основные вычисления удобно свести в таблицу. Сначала в верхние две строки записываем исходные данные. Затем рассчитываем произведения  , затем
, затем и, наконец, суммы в правом столбце:
и, наконец, суммы в правом столбце:
| | -2 | 0 | 3 | 7 | Суммы |
| | 0,4 | 0,1 | 0,3 | 0,2 | 1 |
| | -0,8 | 0 | 0,9 | 1,4 | 1,5 |
| | 1,6 | 0 | 2,7 | 9,8 | 14,1 |
Собственно, почти всё готово. В третьей строке математическое ожидание: 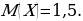 Дисперсию вычислим по формуле:
Дисперсию вычислим по формуле: 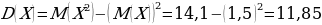 . И, наконец, среднеквадратическое отклонение:
. И, наконец, среднеквадратическое отклонение: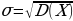 =
=
Заданий для самостоятельного решения:
Пример 1 Дискретная случайная величина задана своим законом распределения:
| | 12 | 16 | 21 | 26 | 30 |
| | 0,2 | 0,1 | 0,4 | a | 0,1 |
Найти её математическое ожидание, дисперсию и среднеквадратическое отклонение.
Численное дифференцирование.
План:
Постановка задачи численного дифференцирования
Численное дифференцирование на основе интерполяционных формул Ньютона
Оценка погрешности дифференцирования с помощью многочлена Ньютона
Численное дифференцирование на основе интерполяционной формулы Лагранжа
Оценка погрешности численного дифференцирования с помощью многочлена Лагранжа
Постановка задачи численного дифференцирования
Функция y = f(x) задана таблицей:
| x | x0 | x1 | ... | xn |
| y | y0 | y1 | ... | yn |
на отрезке [a; b] в узлах 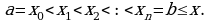 Требуется найти приближенное значение производной этой функции в некоторой точке х* [a; b]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
Требуется найти приближенное значение производной этой функции в некоторой точке х* [a; b]. При этом х* может быть как узловой точкой, так и расположенной между узлами.
Численное дифференцирование на основе интерполяционных формул Ньютона
Считая узлы таблицы равноотстоящими, построим интерполяционный полином Ньютона. Затем продифференцируем его, полагая, что 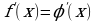 на
на 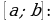
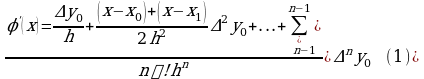
Формула значительно упрощается, если производная ищется в одном из узлов таблицы: 
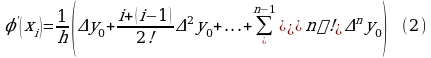
Подобным путём можно получить и производные функции 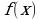 более высоких порядков. Однако, каждый раз вычисляя значение производной функции
более высоких порядков. Однако, каждый раз вычисляя значение производной функции 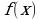 в фиксированной точке х в качестве
в фиксированной точке х в качестве 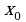 следует брать ближайшее слева узловое значение аргумента.
следует брать ближайшее слева узловое значение аргумента.
Численное дифференцирование на основе интерполяционной формулы Лагранжа
Запишем формулу Лагранжа для равноотстоящих узлов в более удобном виде для дифференцирования: 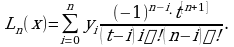 Затем, дифференцируя по х как функцию от , получим:
Затем, дифференцируя по х как функцию от , получим:
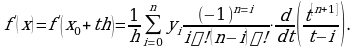
Пользуясь этой формулой можно вычислять приближённые значения производной таблично-заданной функции  в одном из равноотстоящих узлов. Аналогично могут быть найдены значения производных функции
в одном из равноотстоящих узлов. Аналогично могут быть найдены значения производных функции  более высоких порядков.
более высоких порядков.
Численное интегрирование
План:Постановка задачи численного интегрирования
Квадратурные формулы Ньютона-Котеса
Формулы прямоугольников
Формула трапеций
Формула Симпсона
Квадратурные формулы Гаусса
Метод Монте-Карло
Постановка задачи численного интегрирования
Требуется вычислить определённый интеграл вида 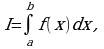 причём функция может быть задана как в виде формулы, так и в виде таблицы.
причём функция может быть задана как в виде формулы, так и в виде таблицы.
Квадратурные формулы Ньютона-Котеса 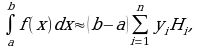 где
где 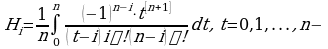 коэффициенты Котеса. Эти формулы дают на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
коэффициенты Котеса. Эти формулы дают на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
Формулы прямоугольников
Пусть требуется вычислить интеграл. Если отрезок интегрирования [a; b] достаточно велик, то нужно разбить его на более мелкие отрезки равной длины 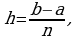 где
где 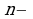 число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла. Что касается построения прямоугольников, то их можно строить по-разному: можно проводить перпендикуляр до пересечения с кривой
число отрезков, и заменяя на каждом из отрезков криволинейную трапецию прямоугольником, вычислить площади этих прямоугольников. Затем полученные площади нужно сложить, эта сумма и будет принята за приближённое значение искомого интеграла. Что касается построения прямоугольников, то их можно строить по-разному: можно проводить перпендикуляр до пересечения с кривой 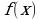 из правого конца каждого отрезка (Рис. 1), можно - из левого конца (Рис. 2)
из правого конца каждого отрезка (Рис. 1), можно - из левого конца (Рис. 2)
|
|
|
В зависимости от этого формулы для вычисления несколько различны и носят название формулы прямоугольников с правыми или левыми ординатами соответственно:
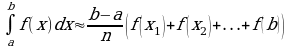
(формула "правых" прямоугольников)
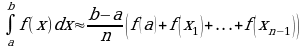
(формула "левых" прямоугольников). Существует ещё формула "средних" прямоугольников:
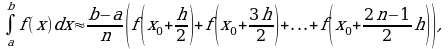
для которой построение прямоугольников осуществляется через середины каждого из отрезков разбиения: 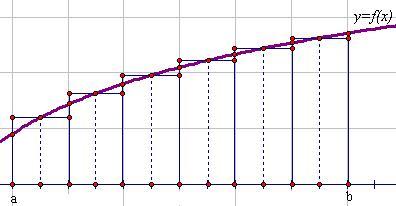
Формула трапеций
| Идея метода аналогична той, что представлена в методе прямоугольников. Отличие заключается в том, что на каждом отрезке разбиения криволинейная трапеция заменяется на обычную трапецию, площадь которой вычисляется по формуле | |
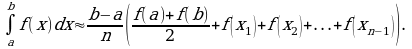
Формула Симпсона
Заменяя на каждом отрезке разбиения часть кривой y = f (x) на параболическую кривую, вычисляя площади получившихся фигур и суммируя их, получим формулу Симпсона:
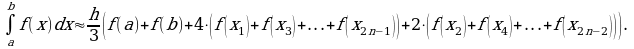
Квадратурные формулы Гаусса
Традиционно при получении квадратурных формул Гаусса в исходном интеграле выполняется замена переменной, переводящая интеграл по отрезку [a; b] в интеграл по отрезку [-1; 1]:
Тогда  Будем использовать линейную интерполяцию подынтегральной функции. Если вместо отрезка [-1; 1] взять в качестве узлов интерполяции подвижные узлы
Будем использовать линейную интерполяцию подынтегральной функции. Если вместо отрезка [-1; 1] взять в качестве узлов интерполяции подвижные узлы 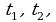 то нужно выбрать эти значения так, чтобы площадь трапеции, ограниченной сверху прямой, проходящей через точки
то нужно выбрать эти значения так, чтобы площадь трапеции, ограниченной сверху прямой, проходящей через точки 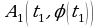 и
и 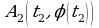 была равной интегралу от любого многочлена некоторой наивысшей степени. Полагая, что это многочлен третьей степени, вычислим
была равной интегралу от любого многочлена некоторой наивысшей степени. Полагая, что это многочлен третьей степени, вычислим  которые получаются равными
которые получаются равными  и , отличаясь лишь нумерацией значений. Далее разбивая отрезок интегрирования на n частей, применяя к каждому из них описанную выше идею, можно получить формулу Гаусса:
и , отличаясь лишь нумерацией значений. Далее разбивая отрезок интегрирования на n частей, применяя к каждому из них описанную выше идею, можно получить формулу Гаусса:
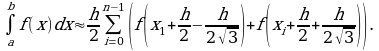
Метод Монте-Карло
| Идея метода: Пусть |
|
отрезком [a; b] оси 
отрезком, принадлежащим прямой  длины
длины 
отрезками, принадлежащими прямым  и
и  заключёнными между осью
заключёнными между осью 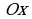 и прямой y = M.
и прямой y = M.
Координаты таких точек вычисляются по формулам:
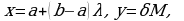 где
где 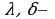 случайные числа из отрезка
случайные числа из отрезка 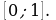
Если найдено таким образом n точек и k из них принадлежит криволинейной трапеции, ограниченной кривой 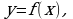 прямыми
прямыми 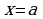 ,
,  и осью
и осью  , то, с учётом того, что при больших n распределение точек по прямоугольнику близко к равномерному, то отношение
, то, с учётом того, что при больших n распределение точек по прямоугольнику близко к равномерному, то отношение 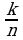 приближённо равно отношению площади криволинейноё трапеции к площади прямоугольника:
приближённо равно отношению площади криволинейноё трапеции к площади прямоугольника: 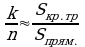 . При этом
. При этом 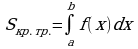 и
и 
Подставляя значения площадей и выражая интеграл, получаем: 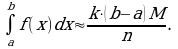


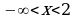

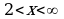


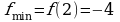
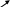
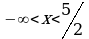
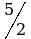



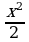
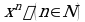
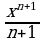
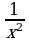
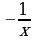
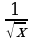
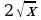 (при
(при 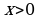 )
)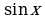

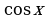
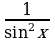
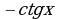
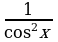
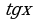
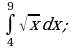
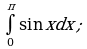
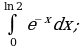
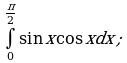

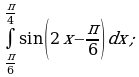
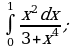


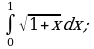
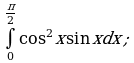
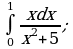
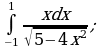
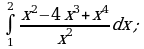
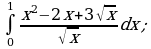
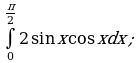
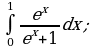
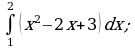
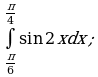
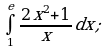
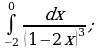
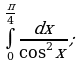
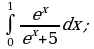
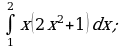
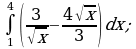
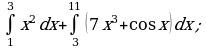
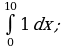


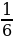
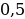
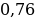
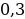

 Рис. 1
Рис. 1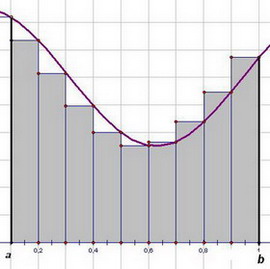 Рис. 2
Рис. 2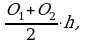 где
где  и
и  основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла:
основания трапеции. Вычисляя и суммируя площади всех трапеций, получаем приближённое значение искомого интеграла: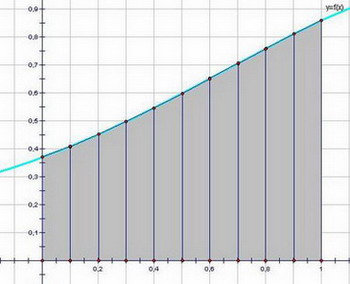
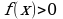 (для простоты рассуждений). Возьмём число M, такое что
(для простоты рассуждений). Возьмём число M, такое что 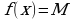 для любого
для любого 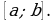 На графике- это прямая
На графике- это прямая 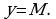 Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном:
Используя счётчик случайных чисел можно получить точки, случайно и равномерно распределённые в прямоугольнике, образованном: