Просмотр содержимого документа
«Лайфхаки в ЕГЭ по математике»
КОНСПЕКТ К ЗАНЯТИЮ №4
@turbo_math




 В
В СЕ ЛАЙФХАКИ В ЕГЭ
СЕ ЛАЙФХАКИ В ЕГЭ
ЗАДАНИЕ №7
 показатель степени
показатель степени
Степенью называется выражение: 𝑎𝑏 основание степени
С натуральным показателем
С целым
показателем
С рациональным
показателем

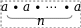

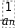

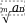
Свойства степеней
Произведение степеней Деление степеней Возведение
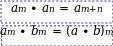
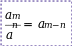
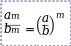 степень в степень
степень в степень
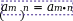

ЗАДАНИЕ №12
ЛАЙФХАК №1
Работает при нахождении наибольшего/наименьшего значения у
функций с натуральным логарифмом
В заданиях с кратким ответом мы должны получать «красивое»
число. Когда в производной есть натуральный логарифм, красивое значение
получится только в случае, если под логарифмом будет единица ln 1 = 0
ПРИМЕР
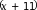 Найдите наибольшее значение функции 𝑦 = ln
Найдите наибольшее значение функции 𝑦 = ln
отрезке [−10,5; 0].
Решение:
12 − 12𝑥 на
Чтобы под логарифмом получилась единица: 𝑥 + 11 = 1 ⇒ 𝑥 = −10
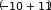
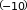 Ищем значение функции в этой точке:
Ищем значение функции в этой точке:
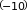 𝑦
𝑦
= ln
12 − 12 ∙
= ln 112 + 120 = 120
Ответ: 120
1

Л

АЙФХАК №2
Работает при нахождении наибольшего/наименьшего значения у функций с экспонентой
В заданиях с кратким ответом мы должны получать «красивое»
число. Когда в производной есть экспонента, красивое значение получится
только в случае, если показатель степени будет равен 0 𝑒0 = 1

ПРИМЕР
Найдите наибольшее значение функции 𝑦 =
отрезке  −3; 2
−3; 2  .
.
Решение:
𝑒𝑥−1 на
Чтобы в показателе экспоненты получился ноль: 𝑥 − 1 = 0 ⇒ 𝑥 = 1
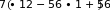
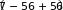 Ищем значение функции в этой точке:
Ищем значение функции в этой точке:
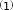 𝑦
𝑦
=
𝑒1−1 =
𝑒0 = 7 ∙ 1 = 7
Ответ: 7

ЛАЙФХАК №3
С уравнением параболы (квадратный трехчлен) в производной
Лайфхак связан с графиком квадратичной функции – параболой.
Если ветви параболы направленны вверх – вершина параболы точка минимума, в которой функция принимает наименьшее значение.
Если ветви параболы направленны вниз – вершина параболы точка максимума, в которой функция принимает наибольшее значение
ПРИМЕР
 Найдите наименьшее значение функции 𝑦 = 𝑥2 + 2𝑥 + 122 на
Найдите наименьшее значение функции 𝑦 = 𝑥2 + 2𝑥 + 122 на
отрезке  −50; 150
−50; 150  .
.
Решение:
Под корнем уравнение параболы, ветви вверх. Значит наименьшее значение
функции будет в точке минимума – вершине параболы.
Формула для нахождения абсциссы вершины параболы: 𝑥 = −𝑏 = −2 = −1
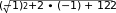
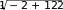
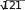 Найдем значение функции в этой точке:
Найдем значение функции в этой точке:
2𝑎 2
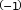 𝑦
𝑦
=
=
=
= 11
Ответ: 11
2







 В
В СЕ ЛАЙФХАКИ В ЕГЭ
СЕ ЛАЙФХАКИ В ЕГЭ показатель степени
показатель степени
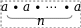

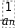
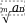
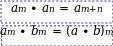
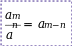
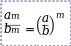 степень в степень
степень в степень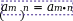
 ЗАДАНИЕ №12
ЗАДАНИЕ №12 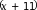 Найдите наибольшее значение функции 𝑦 = ln
Найдите наибольшее значение функции 𝑦 = ln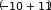
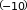 Ищем значение функции в этой точке:
Ищем значение функции в этой точке: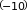 𝑦
𝑦 Л
Л АЙФХАК №2
АЙФХАК №2  ПРИМЕР
ПРИМЕР 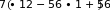
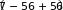 Ищем значение функции в этой точке:
Ищем значение функции в этой точке: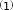 𝑦
𝑦 Найдите наименьшее значение функции 𝑦 = 𝑥2 + 2𝑥 + 122 на
Найдите наименьшее значение функции 𝑦 = 𝑥2 + 2𝑥 + 122 на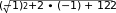
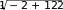
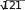 Найдем значение функции в этой точке:
Найдем значение функции в этой точке: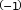 𝑦
𝑦









