Лекция 2.2. Закон распределения дискретной случайной величины.

Электронный курс лекций

«Комбинаторика»

Лекция 2.2. Закон распределения дискретной случайной величины.

к.п.н., преподаватель высшей категории Никитин М.Е. Раменское, 2015

Основные вопросы:

• Понятие случайной величины. Закон распределения случайной величины.
• Числовые характеристики дискретных случайных величин.

Определение

Случайной величиной называется переменная величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.

• Пример

Случайными величинами являются: температура больного в некоторое наугад выбранное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента.

Определение

• Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью , образующие счетное множество (множество, элементы которого могут быть занумерованы).
• Это множество может быть как конечным , так и бесконечным .
• Например , число посетителей аптеки в течение дня, количество яблок на дереве.

Определение

• Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
• Очевидно, что число возможных значений непрерывной случайной величины бесконечно .
• Например : температура больного в фиксированное время суток, масса наугад выбранной таблетки некоторого препарата, рост наугад выбранного студента

ЗАКОН РАСПРЕДЕЛЕНИЯ

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины х 1 , х 2 , х 3 ,… и соответствующими им вероятностями p 1 , р 2 , р 3 ,… .

Закон распределения может быть задан аналитически , в виде таблицы или графически .

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения .

Рассмотрим дискретную случайную величину X с возможными значениями x 1 , х 2 , …, х n . Каждое из этих значений возможно, но не достоверно, и величина X может принять каждое из них с некоторой вероятностью. В результате опыта величина X примет одно из этих значений, т. е. произойдет одно из полной группы несовместных событий.

Обозначим вероятности этих событий буквами р с соответствующими индексами:

Р(Х=х 1 )=р 1 ; Р(Х=х 2 ) = р 2 ; ...; Р(Х = х n ) = р n .

Так как несовместные события образуют полную группу, то сумма вероятностей всех возможных значений случайной величины равна единице

Ряд распределения случайной величины X имеет следующий вид

x i

x 1

p i

x 2

p 1

…

p 2

x n

…

p n

Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению : по оси абсцисс откла­дываются возможные значения случайной величины Х, а по оси ординат — вероятности этих значений Р. Такая фигура называется многоугольником распределения (полигон частот) .

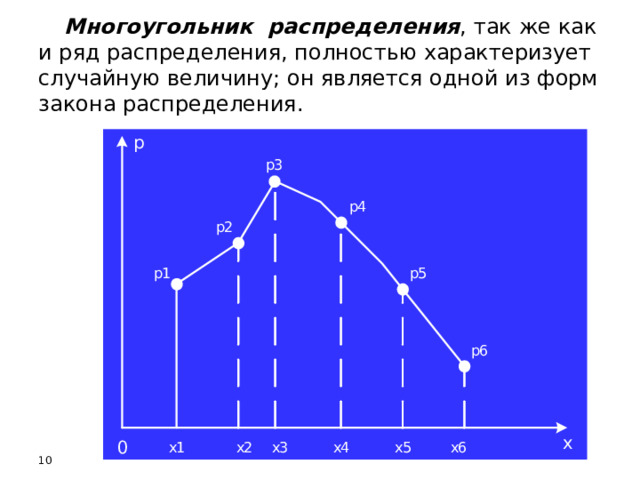
Многоугольник распределения , так же как и ряд распределения, полностью характеризует случайную величину; он является одной из форм закона распределения.

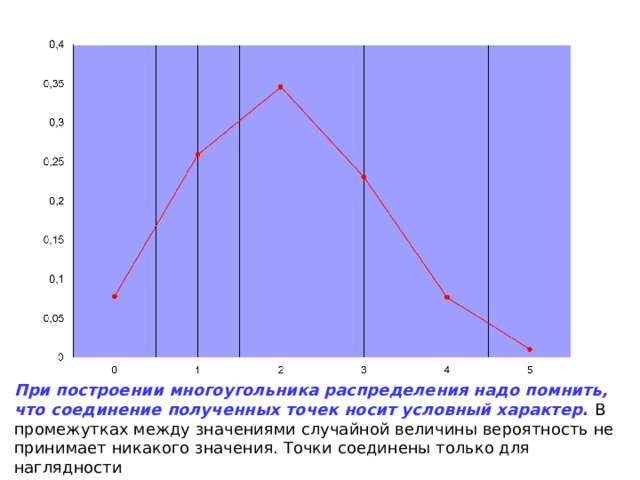
При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер . В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности

Биноминальное распределение

Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p .

Примем число появлений события в каждом из испытаний за некоторую случайную величину Х .

Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.

Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.

Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли .

Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным .

Числовые характеристики дискретных случайных величин

Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений .

, где

Х – прерывная случайная величина ,

М [X] – среднее значение случайной величины,

– возможные значения величины Х,

p 1 , р 2 , р 3 ,…,р n – вероятности значений.

Свойства математического ожидания:

• Математическое ожидание постоянной величины равно самой постоянной.
• Постоянный множитель можно выносить за знак математического ожидания.

Свойства математического ожидания:

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых.

Пусть производится п независимых испытаний, вероятность появления события А в которых равна р .

  Теорема. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании .

Дисперсия

Дисперсией (рассеиванием) D ( X ) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Теорема

Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания .

Свойства дисперсии:

• Дисперсия постоянной величины равна нулю.

• Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

Свойства дисперсии:

• Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

• Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

Теорема

Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в каждом испытании.

Среднее квадратическое отклонение

Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии.

Теорема

Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин.

Домашнее задание:

1. конспект лекции

СВР: Составить опорный конспект по теории

Задачи