Лекция 6. "Исследование функций и построение графиков"

Исследование функций и построение графиков

к.п.н., преподаватель высшей категории Никитин М.Е. Раменское, 2021

Теоретический материал

Содержание

1) Область определения функции

2) Свойства функции (четность, нечетность, периодичность)

4) Точки пересечения функции с осями координат

5) Непрерывность функции. Характер точек разрыва

6) Асимптоты

7) Экстремумы функции. Исследование функции на монотонность

8) Выпуклость функции. Точки перегиба

Область определения функции

Определение . Областью определения функции называется множество значений независимой переменной, при которых функция определена.

Примеры.

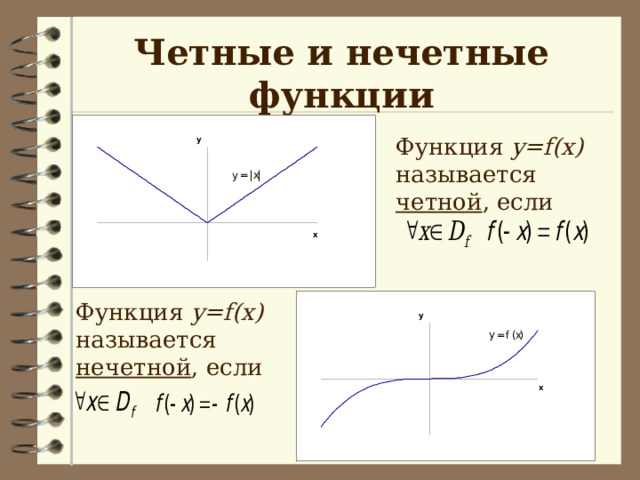
Четные и нечетные функции

Функция y=f(x) называется четной , если

Функция y=f(x) называется нечетной , если

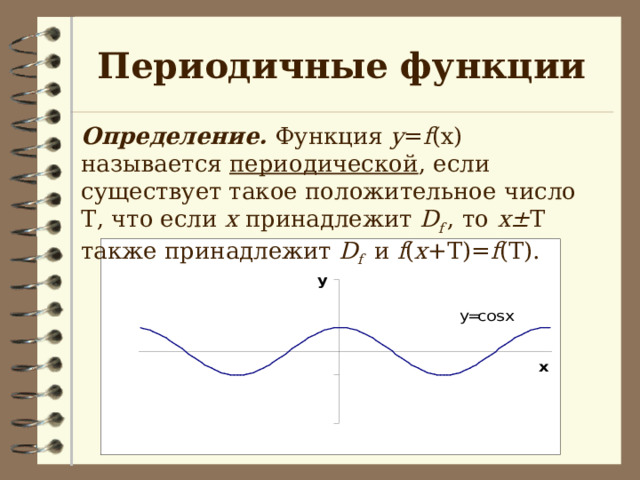
Периодичные функции

Определение. Функция y = f (x) называется периодической , если существует такое положительное число Т , что если х принадлежит D f , то х± Т также принадлежит D f и f ( x +T)= f (T).

Точки пересечения с осями координат

При исследовании функции необходимо найти координаты точек пересечения графика функции с осями координат.

Абсциссы точек пересечения графика функции с осью Ох находятся из системы уравнений у= f ( x ) и у= 0, а ординаты точек пересечения графика функции с осью Оу находятся из системы уравнений у= f (x) и х= 0.

• При исследовании функции необходимо найти координаты точек пересечения графика функции с осями координат. Абсциссы точек пересечения графика функции с осью Ох находятся из системы уравнений у= f ( x ) и у= 0, а ординаты точек пересечения графика функции с осью Оу находятся из системы уравнений у= f (x) и х= 0.
• При исследовании функции необходимо найти координаты точек пересечения графика функции с осями координат. Абсциссы точек пересечения графика функции с осью Ох находятся из системы уравнений у= f ( x ) и у= 0, а ординаты точек пересечения графика функции с осью Оу находятся из системы уравнений у= f (x) и х= 0.

Непрерывность Характер точек разрыва

Функция у= f(x) называется непрерывной в точке х 0 , если функция определена в точке х 0 и предел функции в точке х 0 равен значению функции в точке х 0 .

Функции, непрерывные в каждой точке из области определения функции, называются непрерывными функциями .

Примеры непрерывных функций: y=cosx , y=sinx , y=e x , y=P n (x) ( многочлен степени n ) .

Точки разрыва функции

Определение. Точкой разрыва функции называется точка из области определения функции, в которой функция не является непрерывной.

Пример. Функция

size 12{ {} cSub {} } {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAAfQAAAAT AwAACAAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAAPMAAAASAwAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAJUAAQAEAAAAAAAAAJYAAQACAAAACQCMAAEAAAAAAA== lim x → 0 f ( x ) = lim x → 0 sin x x = 1 , f ( 0 ) = 0 size 12{ { size 24{"lim"} } cSub { size 8{x rightarrow 0} } f \( x \) = { size 24{"lim"} } cSub { size 8{x rightarrow 0} } { {"sin"x} over {x} } =1,`f \( 0 \) =0} {} VkNMTVRGAQAxAAAAAAAAAAEAGwAAAAAAAAAAAAAAAAABAAAAAQAAAAEAAAABAAAAATYeAAAe BQAAwAAAAJYAAQACAAAACQCLAAEAAgAAAP//gQABABAAAAAAAAAAAAAAADUeAAAdBQAAlQAB AAQAAAAAAAAAlgABAAIAAAAJAIsAAQACAAAAHwCKAAEAPgAAAAMAOAAAAAwARGVqYVZ1IFNl cmlmAAAAAAAATAMAAAAAAAAAAAUAAAAAAAAA/wMAAAAAAAAAAQD/AwAAAAAAiAABAAIAAAAB AIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAHQAAAGoAAAAaAwAAAwBsaW08BQAAAAAD AAMAbABpAG0AjAABAAAAAACLAAEAAgAAAB8AigABAD4AAAADADgAAAAMAERlamFWdSBTZXJp ZgAAAAAAABkBAAAAAAAAAAAFAAAAAAACAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCH AAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADcAQAA3AQAAAEAeJ4AAAAAAAEAAQB4 AIwAAQAAAAAAiwABAAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9sAAAAAAAAGQEA AP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAQD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA//// /wCGAAEABAAAAAAAAAByAAIAGgAAALACAADcBAAAAQAAAJIh3gAAAAAAAQABAJIhjAABAAAA AACLAAEAAgAAAB8AigABAD4AAAADADgAAAAMAERlamFWdSBTZXJpZgAAAAAAABkBAAAAAAAA AAAFAAAAAAAAAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgAB AAQAAAAAAAAAcgACABcAAACeAwAA3AQAAAEAMLMAAAAAAAEAAQAwAIwAAQAAAAAAiwABAAIA AAAfAIoAAQA+AAAAAwA4AAAADABEZWphVnUgU2VyaWYAAAAAAACmAQAAAAAAAAAABQAAAAAA AgD/AwAAAAAAAAABAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAA AHIAAgAXAAAA/wUAABoDAAABAGacAAAAAAABAAEAZgCMAAEAAAAAAIsAAQACAAAAHwCKAAEA PAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAA AAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAADS BgAAGgMAAAEAAAAoAI8AAAAAAAEAAQAoAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA+AAAAAwA4 AAAADABEZWphVnUgU2VyaWYAAAAAAACmAQAAAAAAAAAABQAAAAAAAgD/AwAAAAAAAAABAP8D AAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAApgcAABoD AAABAHjuAAAAAAABAAEAeACMAAEAAAAAAIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3Bl blN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQAC AAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAADJCAAAGgMAAAEAAAApAI8A AAAAAAEAAQApAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9s AAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAAAQD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAGgAAAE0JAAAaAwAAAQAAAD0ATwEAAAAAAQAB AD0AjAABAAAAAACLAAEAAgAAAB8AigABAD4AAAADADgAAAAMAERlamFWdSBTZXJpZgAAAAAA AEwDAAAAAAAAAAAFAAAAAAAAAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAA AP////8AhgABAAQAAAAAAAAAcgACAB0AAADACgAAGgMAAAMAbGltPAUAAAAAAwADAGwAaQBt AIwAAQAAAAAAiwABAAIAAAAfAIoAAQA+AAAAAwA4AAAADABEZWphVnUgU2VyaWYAAAAAAAAZ AQAAAAAAAAAABQAAAAAAAgD/AwAAAAAAAAABAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/ ////AIYAAQAEAAAAAAAAAHIAAgAXAAAAMgwAANwEAAABAHieAAAAAAABAAEAeACMAAEAAAAA AIsAAQACAAAAHwCKAAEAPAAAAAMANgAAAAoAT3BlblN5bWJvbAAAAAAAABkBAAD//wAAAAAF AAAAAAAAAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQA AAAAAAAAcgACABoAAADrDAAA3AQAAAEAAACSId4AAAAAAAEAAQCSIYwAAQAAAAAAiwABAAIA AAAfAIoAAQA+AAAAAwA4AAAADABEZWphVnUgU2VyaWYAAAAAAAAZAQAAAAAAAAAABQAAAAAA AAD/AwAAAAAAAAABAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAA AHIAAgAXAAAA2Q0AANwEAAABADCzAAAAAAABAAEAMACMAAEAAAAAAIsAAQACAAAAHwCKAAEA PgAAAAMAOAAAAAwARGVqYVZ1IFNlcmlmAAAAAAAApgEAAAAAAAAAAAUAAAAAAAAA/wMAAAAA AAAAAQD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAHQAA ADoQAAARAgAAAwBzaW5vAgAAAAADAAMAcwBpAG4AjAABAAAAAACLAAEAAgAAAB8AigABAD4A AAADADgAAAAMAERlamFWdSBTZXJpZgAAAAAAAKYBAAAAAAAAAAAFAAAAAAACAP8DAAAAAAAA AAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABcAAADq EgAAEQIAAAEAeO4AAAAAAAEAAQB4AIwAAQAAAAAAiwABAAIAAAAfAIUAAQAFAAAAAAAAAAGE AAEABQAAAAAAAAAAigABADwAAAADADYAAAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAA BQAAAAAAAAD/AwAAAAAAAAABAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAE AAAAAAAAAGcAAQAQAAAAVBAAAJUCAAAvFAAAqQIAAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA+ AAAAAwA4AAAADABEZWphVnUgU2VyaWYAAAAAAACmAQAAAAAAAAAABQAAAAAAAgD/AwAAAAAA AAABAP8DAAAAAACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAA xxEAAD0EAAABAHjuAAAAAAABAAEAeACMAAEAAAAAAIsAAQACAAAAHwCKAAEAPAAAAAMANgAA AAoAT3BlblN5bWJvbAAAAAAAAKYBAAD//wAAAAAFAAAAAAAAAP8DAAAAAAAAAAEA/wMAAAAA AIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAAcgACABoAAABCFAAAGgMAAAEA AAA9AE8BAAAAAAEAAQA9AIwAAQAAAAAAiwABAAIAAAAfAIoAAQA+AAAAAwA4AAAADABEZWph VnUgU2VyaWYAAAAAAACmAQAAAAAAAAAABQAAAAAAAAD/AwAAAAAAAAABAP8DAAAAAACIAAEA AgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAXAAAAmhUAABoDAAABADEMAQAA AAABAAEAMQCMAAEAAAAAAIsAAQACAAAAHwCKAAEAPgAAAAMAOAAAAAwARGVqYVZ1IFNlcmlm AAAAAAAApgEAAAAAAAAAAAUAAAAAAAIA/wMAAAAAAAAAAQD/AwAAAAAAiAABAAIAAAABAIcA AQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAANcWAAAaAwAAAQAshgAAAAAAAQABACwA jAABAAAAAACLAAEAAgAAAB8AigABAD4AAAADADgAAAAMAERlamFWdSBTZXJpZgAAAAAAAKYB AAAAAAAAAAAFAAAAAAACAP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP// //8AhgABAAQAAAAAAAAAcgACABcAAADgFwAAGgMAAAEAZpwAAAAAAAEAAQBmAIwAAQAAAAAA iwABAAIAAAAfAIoAAQA8AAAAAwA2AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAAAAUA AAAAAAAA/wMAAAAAAAAAAQD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAA AAAAAAByAAIAGgAAAM4YAAAaAwAAAQAAACgAjwAAAAAAAQABACgAjAABAAAAAACLAAEAAgAA AB8AigABAD4AAAADADgAAAAMAERlamFWdSBTZXJpZgAAAAAAAKYBAAAAAAAAAAAFAAAAAAAA AP8DAAAAAAAAAAEA/wMAAAAAAIgAAQACAAAAAQCHAAEABQAAAP////8AhgABAAQAAAAAAAAA cgACABcAAACHGQAAGgMAAAEAMAwBAAAAAAEAAQAwAIwAAQAAAAAAiwABAAIAAAAfAIoAAQA8 AAAAAwA2AAAACgBPcGVuU3ltYm9sAAAAAAAApgEAAP//AAAAAAUAAAAAAAAA/wMAAAAAAAAA AQD/AwAAAAAAiAABAAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAGgAAAKoa AAAaAwAAAQAAACkAjwAAAAAAAQABACkAjAABAAAAAACLAAEAAgAAAB8AigABADwAAAADADYA AAAKAE9wZW5TeW1ib2wAAAAAAACmAQAA//8AAAAABQAAAAAAAAD/AwAAAAAAAAABAP8DAAAA AACIAAEAAgAAAAEAhwABAAUAAAD/////AIYAAQAEAAAAAAAAAHIAAgAaAAAASRsAABoDAAAB AAAAPQBPAQAAAAABAAEAPQCMAAEAAAAAAIsAAQACAAAAHwCKAAEAPgAAAAMAOAAAAAwARGVq YVZ1IFNlcmlmAAAAAAAApgEAAAAAAAAAAAUAAAAAAAAA/wMAAAAAAAAAAQD/AwAAAAAAiAAB AAIAAAABAIcAAQAFAAAA/////wCGAAEABAAAAAAAAAByAAIAFwAAAKEcAAAaAwAAAQAwDAEA AAAAAQABADAAjAABAAAAAACVAAEABAAAAAAAAACWAAEAAgAAAAkAjAABAAAAAAA=

разрывна в 0, так как

Классификация точек разрыва Точки устранимого разрыва

Если в точке х 0 существуют конечные односторонние пределы функции, равные между собой, но не равные значению функции в точке х 0 , то точка х 0 называется точкой устранимого разрыва .

Классификация точек разрыва Точки скачка

Если в точке х 0 существуют конечные односторонние пределы функции, не равные между собой, то точка х 0 называется точкой скачка (точкой разрыва I рода) .

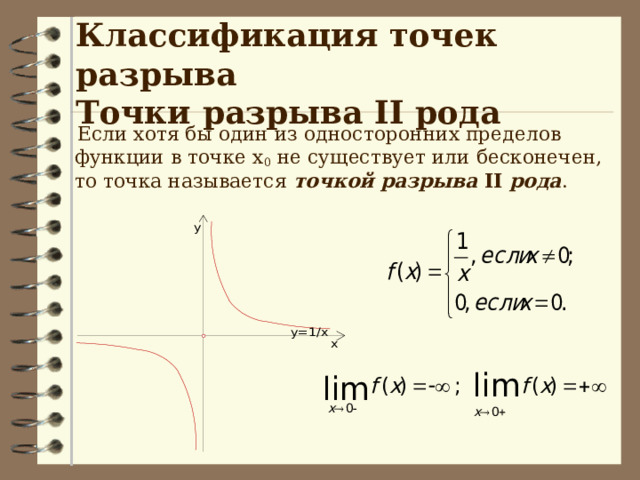
Классификация точек разрыва Точки разрыва II рода

Если хотя бы один из односторонних пределов функции в точке х 0 не существует или бесконечен, то точка называется точкой разрыва II рода .

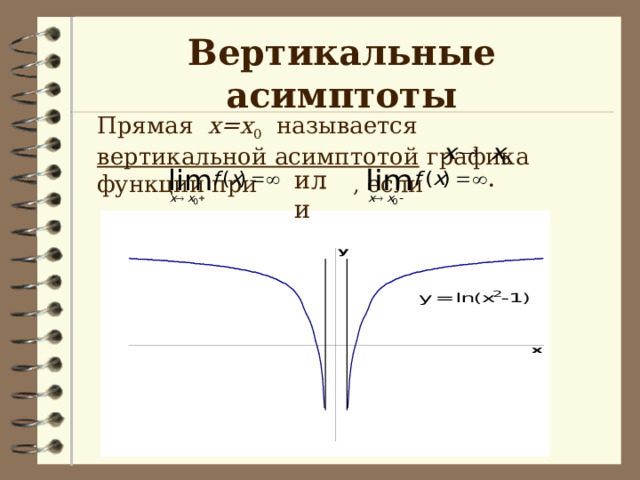
Вертикальные асимптоты

Прямая х=х 0 называется вертикальной асимптотой графика функции при , если

или

.

Наклонные асимптоты

Если существует прямая y=kx+b такая, что

, то эта прямая называется

асимптотой графика функции f при

.

Для того чтобы прямая y=kx+b была асимптотой, необходимо и достаточно, чтобы выполнялись следующие условия:

,

.

f ( x 0 ) ). Точки минимума и точки максимума функции называются точками экстремума функции. Необходимое условие экстремума . Пусть точка х 0 - точка экстремума функции. Тогда либо производная функции в этой точке равна 0, либо не существует. " width="640"

Экстремумы функции

Пусть функция f ( x ) определена и непрерывна на интервале ( а , b ). Точка х 0 интервала ( а , b ) называется точкой строгого максимума (минимума) функции f ( x ) , если в некоторой проколотой окрестности точки х 0 f ( x )f ( x 0 ) ( f ( x ) f ( x 0 ) ).

Точки минимума и точки максимума функции называются точками экстремума функции.

Необходимое условие экстремума . Пусть точка х 0 - точка экстремума функции. Тогда либо производная функции в этой точке равна 0, либо не существует.

0 ( f '( x )0) в ( а , b ) , то функция f ( x ) строго возрастает (строго убывает) в ( а , b ) . Рассмотрим функцию f(x) = x + 1|x Критические точки функции х =±1. f '( x )0 при х х 1; f '( x )x x функция возрастает функция убывает " width="640"

Исследование функции на монотонность

Известно, что если f '( x )0 ( f '( x )0) в ( а , b ) , то функция f ( x ) строго возрастает (строго убывает) в ( а , b ) .

Рассмотрим функцию f(x) = x + 1|x

Критические точки функции х =±1. f '( x )0 при х х 1; f '( x )x x

функция возрастает

функция убывает

Выпуклость функции

Функция у= f ( х ), определенная на интервале ( а , b ), называется выпуклой вверх ( вниз ) в интервале ( а , b ), если для любых х 1 и х 2 из интервала ( а , b ) из того, что х 1 х 2 , следует, что часть графика функции между точками ( х 1 , f ( х 1 )) и ( х 2 , f ( х 2 )) лежит выше (ниже) хорды, соединяющей эти точки.

Выпуклость функции. Точки перегиба

Также говорят, что график функции f ( x ) имеет на интервале ( a , b ) выпуклость, направленную вниз (вверх), если график этой функции в пределах ( a , b ) лежит не ниже (не выше) любой своей касательной.

Если график функции в точке ( х 0 , f ( x 0 )) переходит с одной стороны касательной на другую, то точка х 0 называется точкой перегиба функции f ( x ).

0 , то на интервале ( а , b ) функция выпукла вниз, и если на интервале f ''( x ) на интервале ( а , b ) функция выпукла вверх. Достаточное условие строгой выпуклости функции Если в левой и правой полуокрестностях некоторой точки х 0 f ''( x ) имеет противоположные знаки, то точка х 0 – точка перегиба функции. " width="640"

Достаточные условия выпуклости функции и существования точек перегиба

Достаточное условие строгой выпуклости функции

Если на интервале ( а , b ) f ''( x )0 , то на интервале ( а , b ) функция выпукла вниз, и если на интервале f ''( x )

на интервале ( а , b ) функция выпукла вверх.

Достаточное условие строгой выпуклости функции

Если в левой и правой полуокрестностях некоторой точки х 0 f ''( x ) имеет противоположные знаки, то точка х 0 – точка перегиба функции.

Практический материал

Исследуем функцию и построим её график.

1). Поскольку знаменатель положителен при всех , область определения функции - вся ось

2). Функция f(x) - нечётная, поскольку при смене знака x числитель меняет знак, а знаменатель остаётся без изменения, откуда f(-x) = - f(x) . Следовательно, график функции симметричен относительно начала координат.

Периодической функция не является.

3). Поскольку область определения этой элементарной функции -- вся вещественная ось, вертикальных асимптот график не имеет.

4). Найдём наклонные асимптоты при в виде

. Имеем:

Таким образом, асимптотой как при , так и при

служит прямая .

0 при x0 и f(x) при x . " width="640"

5). Найдём точки пересечения с осями координат. Имеем:

f(0) = 0 , причём x=0 - единственное решение уравнения f(x) = 0 . Значит, график y = f(x) пересекает сразу и ось O x , и ось O y в начале координат.

Очевидно, что f(x)0 при x0 и f(x) при x .

6) Найдём производную:

Очевидно, что f´(x) ≥ 0 при всех ; единственная точка, в которой f´(x) = 0 - это x=0 . Значит, функция f(x) возрастает на всей оси O x , а в стационарной точке x=0 имеет горизонтальную касательную.

0 на интервалах и - на этих интервалах функция выпукла. На интервалах и выполняется обратное неравенство f’’(x) , здесь функция вогнута. Все три точки, в которых f’’(x)=0 , то есть точки - √3, 0, √3, являются точками перегиба. " width="640"

7) Найдём вторую производную:

Знаменатель этой дроби положителен при всех x . Числитель имеет корни x=0 и x=±√3 , при этом f’’(x)0 на интервалах и - на этих интервалах функция выпукла. На интервалах и выполняется обратное неравенство f’’(x) , здесь функция вогнута. Все три точки, в которых f’’(x)=0 , то есть точки - √3, 0, √3, являются точками перегиба.

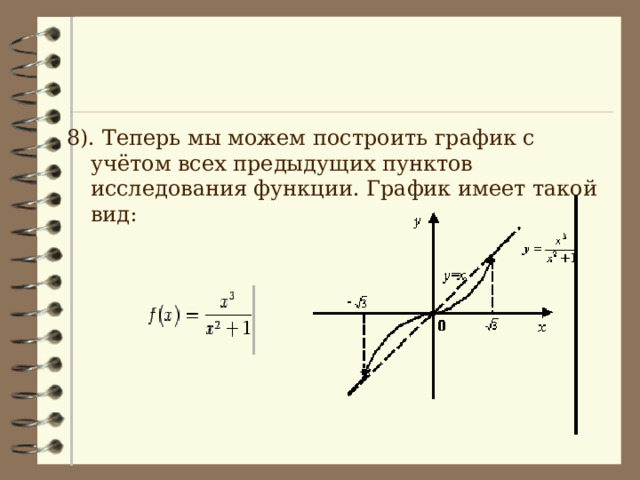
8). Теперь мы можем построить график с учётом всех предыдущих пунктов исследования функции. График имеет такой вид:

Исследуем функцию f(x) = (x 2 – 2x)e x и построим её график.

1). Ясно, что D(f) = R , поскольку оба сомножителя в выражении f(x) определены при любом . Область значений E(f) найдём после того, как отыщем локальные экстремумы функции.

2). Функция не является ни чётной, ни нечётной; не является она и периодической.

3). Область определения не имеет граничных точек, значит, нет и вертикальных асимптот графика.

4) Будем искать наклонные асимптоты в виде y = kx + b. Коэффициент k найдём по формуле : при имеем

так что при асимптоты нет, причём функция f(x) стремится к при .

При имеем:

Теперь найдём значение b по формуле .

Имеем:

Таким образом, k=0 и b=0 , так что при асимптота имеет уравнение y=0 , то есть совпадает с осью O x .

5). Точка пересечения с осью O y равна f(0)=0 . Заодно нашли одну точку пересечения с осью O x . Чтобы найти все точки пересечения графика с осью O x , решаем уравнение f(x) = (x 2 – 2x)e x . Поскольку e x ≠ 0 , решаем уравнение , откуда получаем два корня: x=0 и x=2 . Так как точек разрыва нет, то имеем три интервала знакопостоянства функции: , и

.

0 при всех x . Значит, f(x)0 при и при и f(x) при . 6) Вычислим производную: Интервалы возрастания задаются неравенством f‘(x)0 , то есть, с учётом того, что e x 0 , неравенством x 2 – 2x0 . Решением этого неравенства служит множество На этих двух интервалах функция возрастает. Легко видеть, что на интервале выполняется неравенство f‘(x) , следовательно, это интервал убывания функции. В точке -√2 возрастание сменяется убыванием, значит, точка   -√2 - точка локального максимума. " width="640"

Знак функции определяется множителем x 2 – 2x , поскольку e x 0 при всех x . Значит, f(x)0 при и при и f(x) при .

6) Вычислим производную:

Интервалы возрастания задаются неравенством f‘(x)0 , то есть, с учётом того, что e x 0 , неравенством x 2 – 2x0 . Решением этого неравенства служит множество

На этих двух интервалах функция возрастает. Легко видеть, что на интервале выполняется неравенство f‘(x) , следовательно, это интервал убывания функции. В точке -√2 возрастание сменяется убыванием, значит, точка   -√2 - точка локального максимума.

Значение функции в этой точке равно

В точке √2 убывание сменяется возрастанием, значит, точка √2 -- точка локального минимума функции. Значение функции в точке минимума таково:

Теперь мы можем примерно представить, как идёт график функции:

Эскиз графика

функции f(x)

0 . Решением этого квадратного неравенства служит объединение интервалов и . На этих интервалах функция выпукла. " width="640"

Становится очевидно, что область значений функции -- это

7) По эскизу графика видно, что где-то в местах, обведённых кружочками, должно смениться направление выпуклости, то есть должны быть точки перегиба. Для исследования этого найдём вторую производную:

Решим неравенство , эквивалентное неравенству x 2 +2x-20 . Решением этого квадратного неравенства служит объединение интервалов и . На этих интервалах функция выпукла.

Ясно, что на интервале функция будет вогнутой. Тем самым точки и   -- это точки перегиба. Значения функции в точках перегиба такие:

8). Осталось построить окончательный чертёж:

График функции (x 2 – 2x)e x .