8
ТЕМА «Основы представления информации в компьютере»
Понятие о системах счисления.
Потребность в записи чисел появилась в очень древние времена, как только люди научились считать. Известно множество способов представления чисел. В любом случае число изображается символом или группой символов.
Количество предметов изображалось нанесением черточек или засечек на какой-либо твердой поверхности: камне, глине и т.д. Люди рисовали палочки на стенах и делали зарубки на костях животных или ветках деревьев, завязывали узелки. Позднее люди вынуждены стали группировать, как вы это сейчас делаете, сотнями, десятками, единицами. И для того, чтобы правильно читать и записывать числа были придуманы СС
Система счисления – это совокупность приемов и правил для обозначения и наименования чисел.
Алфавит системы счисления – это множество всех символов (знаков), используемых для записи чисел в данной системе счисления.
Цифры – это любой символ (знак), входящий в алфавит данной системы счисления.
Основание – количество цифр в позиционной системе счисления.

Системы счисления



Непозиционные
Позиционные
Система счисления называется непозиционной – когда значения цифры не зависит от её положения в числе.
Системы счисления, в которых значение каждой цифры зависит от её положения (позиции) в записи числа называются позиционными системами счисления.
Основные достоинства любой позиционной системы счисления:
Возможно множество позиционных систем, так как за основание системы счисления можно принять любое число, не меньшее 2. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, восьмеричная, шестнадцатеричная и так далее).

Рис.1
Алгоритм перевода чисел в десятичную систему счисления
Для перевода числа из какой-либо системы счисления в десятичную необходимо:
1) пронумеровать разряды числа справа налево, начиная с нуля;
2) умножить каждую цифру числа на основание его системы счисления, возведенное в степень номера этого разряда;
3) сложить полученные числа.
(метод умножения)
Пример 1: Перевести двоичные числа 111012, 10112, 100000002в десятичные:
Решение:
1).
Разряды 4 3 2 1 0
1 1 1 0 12 = 1*20+ 0*21+1*22+1*23+1*24=
Теперь вычислим полученную сумму:
= 1 + 0 + 4 + 8 + 16 = 2910
Итак, из исходного двоичного числа 11101 получили десятичное число 29.
2). из исходного двоичного числа 10112 – получим десятичное число 1110
3 2 1 0
1 0 1 12 = 1*2 + 1*2
+ 1*2 + 0*2
+ 0*2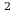 +1*2
+1*2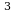 = 1 + 2 + 0 + 8 = 1110
= 1 + 2 + 0 + 8 = 1110
3). 1 0 0 0 0 0 0 0 = 1* 2 = 12810
= 12810
Пример 2: 3AF16 = 3*162 + 10*161 + 15*160= 768+160+15 = 94310.
Пример 3: 77648 = 7*83 + 7*82 + 6*81 + 4*80= 3584 + 448 + 48 + 4 = 408410.
Алгоритм перевода чисел из десятичной системы счисления в любую систему счисления.
Для перевода десятичного числа в другую систему счисления необходимо:
делить нацело с остатком число на нужное основание системы счисления;
получившееся частное (целое) тоже делить нацело с остатком на это же основание;
продолжать деление до тех пор, пока частное не получится равное одному;
выписать остатки в порядке, обратном их получению.
(метод деления)
Пример 1: Число 2210 перевести в двоичную систему счисления.
Решение:
 Ответ: 101102
Ответ: 101102
Пример 2: Число 57110 перевести в восьмеричную систему счисления.
Решение:
 Ответ: 10738
Ответ: 10738
Пример 3: Число 746710 перевести в шестнадцатеричную систему счисления.
Решение:

Ответ:746710 =1D2B16
Алгоритм перевода чисел из двоичной системы счисления в восьмеричную систему счисления.
Сгруппировать разряды группами по 3 числа, справа налево
Затем каждой группе поставить в соответствие ее восьмеричный эквивалент, если цифры обозначены двумя цифрами добавить нужное количество 0 впереди числа, в целой части и сзади, в десятичной части (см. таблицу соответствия).
Записать получившиеся цифры в том же порядке, в котором записаны группы разрядов.
(метод триад)
Пример 1:
Перевести 10111001102 в восьмеричную систему счисления:
Решение
Ответ: 10111001102=13468
Пример 2: Число 10010112 перевести в восьмеричную систему счисления.

Алгоритм перевода чисел из двоичной системы счисления в шестнадцатеричную систему счисления.
разбить данное число (в целой части справа налево, и слева направо в десятичной части) на группы по 4 цифры в каждой (в случае необходимости дополнив старшую тетраду нулями);
рассмотреть каждую группу и записать ее соответствующей цифрой шестнадцатеричной системы счисления.
(метод тетрад)
Пример 1: Перевести 1011100110002 в шестнадцатеричную системы счисления:
Решение
Ответ: 1011100110002=В9816
Пример 2. Число 10111000112 перевести в шестнадцатеричную систему счисления.

Алгоритм перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления.
Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления (см. таблицу соответствия).
Пример 1: Число 5318 перевести в двоичную систему счисления.
Решение: 101 011 0012
Пример 2: Число 53216 перевести в двоичную систему счисления.
Решение: 0101 0011 00102
Пример 3: Число ЕЕ816 перевести в двоичную систему счисления.
Решение: 1110 1110 10002
Алгоритм перевода чисел из восьмеричной в шестнадцатеричную систему счисления.
Правило: При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.
(метод посредника)
Пример 1. Число FEA16 перевести в восьмеричную систему счисления.

Пример 2. Число 66358 перевести в шестнадцатеричную систему счисления.

КОНТРОЛЬНЫЕ ВОПРОСЫ:
Дать определения системы счисления, основания системы счисления, алфавит.
Какие классы систем счисления принято выделять? Чем они отличаются?
Сформулировать правило перевода двоичных чисел в десятичные.
Сформулировать правило перевода десятичных чисел в двоичные.
Сформулировать правило перевода шестнадцатеричных чисел в десятичные.
Сформулировать правило перевода восьмеричных чисел в двоичные.
Приложение 1.
Справочный материал
Значения основания Х в степени n:
Степени числа 2:
2 =1 2
=1 2 =2 2
=2 2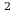 =4 2
=4 2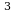 =8 2
=8 2 =16 2
=16 2 =32
=32
2 =64 2
=64 2 =128 2
=128 2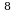 =256 2
=256 2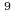 =512 2
=512 2 =1024
=1024
Степени числа 8:
8 =1 8
=1 8 =8 8
=8 8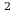 =64 8
=64 8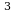 =512 8
=512 8 =4096 8
=4096 8 =32768
=32768
Степени числа 16:
16 =1 16
=1 16 =16 16
=16 16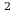 =256 16
=256 16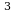 =4096 16
=4096 16 =65536
=65536
Таблица соответствия цифр в различных системах счисления
| Системы счисления |
| 10 | 2 | 8 | 16 |
|
|
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 |
| 8 |
| 9 | 1001 |
| 9 |
| 10 | 1010 |
| A |
| 11 | 1011 |
| B |
| 12 | 1100 |
| C |
| 13 | 1101 |
| D |
| 14 | 1110 |
| E |
| 15 | 1111 |
| F |









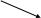



 + 1*2
+ 1*2 + 0*2
+ 0*2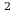 +1*2
+1*2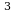 = 1 + 2 + 0 + 8 = 1110
= 1 + 2 + 0 + 8 = 1110 = 12810
= 12810 Ответ: 101102
Ответ: 101102 Ответ: 10738
Ответ: 10738


 =16 2
=16 2 =32
=32  =64 2
=64 2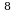 =256 2
=256 2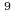 =512 2
=512 2 =1024
=1024









