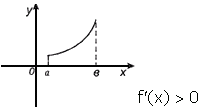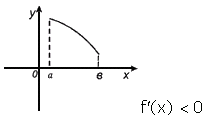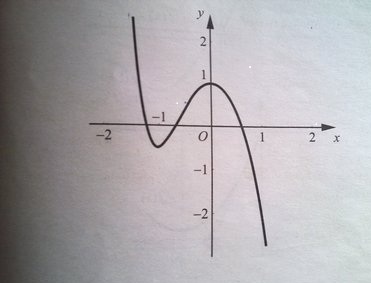Россия, Балаково
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.10.2022 17:18
Водяхина Наталья Владимировна
Преподаватель математики
8 098
5 851 
Местоположение
Специализация
Лекция по теме "Применение производной"
Категория:
Математика
01.11.2021 18:28
Просмотр содержимого документа
«Лекция по теме "Применение производной"»
ТП 211 на 0211.21 г. законспектировать лекцию! Прислать на почту: [email protected]
Тема: Применение производной к исследованию функций и построению графиков. Наибольшее и наименьшее значения функции
Достаточное условие возрастания функции
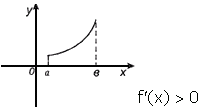
Если в каждой точке интервала (a, b) f /(x)0, то функция f(x) возрастает на этом интервале.
Достаточное условие убывания функции.
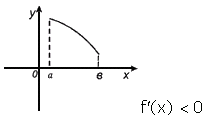
Если в каждой точке интервала (a, b) f /(x), то функция f(x) убывает на этом интервале.
Определение: точка x0 называется критической точкой функции f(x), если
1) x0 – внутренняя точка области определения f(x) ;
2) f /(x0)=0 или f /(x0) не существует.
Необходимое условие экстремума:
Если x0– точка экстремума функции f(x), то эта точка является критической точкой данной функции.
Достаточное условие экстремума:
Если при переходе через точку x0 производная функции меняет знак, то x0 – точка экстремума функции f(x).
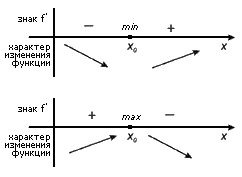
Примеры экстремумов:
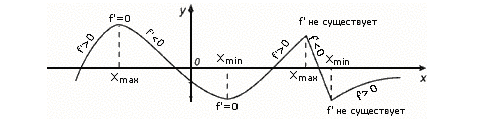
Схема исследования функции:
1. Найти область определения функции (Указать множество значений переменной х, при которых данная функция определена);
2. Найти производную функции;
3. Критические точки, решив уравнение f /(x) = 0;
4. Найти промежутки монотонности (Если f /(x) 0, то функция возрастает, если
f /(x) , то функция убывает);
5. Записать точки экстремума и значения функции в них;
6. Таблица;
7. Дополнительные точки (если это возможно);
8. Построение графика.
Образцы решений
Задание 1. Постройте график функции у (х) = х3 - 2х2 + х.
Решение.
1. Область определения D(f) = R.
2. Найдем производную f'(x) = (х3 - 2х2 + х )' = Зх2- 4х +1.
3. Найдем критические точки, решив уравнение f'(x) = 0.
Зх2- 4х + 1 = 0,
(Зх-1) (х-1) = 0
х1 =1, х2= 1/3
4. Найдем промежутки возрастания и убывания, используя метод интервалов и правило чередования знаков.
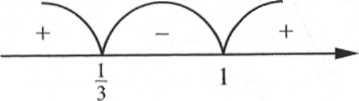
Функция возрастает на промежутках: (-∞, 1/3) и (1,+ ∞), так как
f'(x)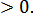
Так как f'(x) на промежутке (1/3, 1), значит, функция убывает на этом промежутке.
5. При переходе через точку х = 1/3 знак производной меняется с «+» на «-», значит, это точка максимума. При переходе через точку х = 1 знак производной меняется с «-» на «+», значит, это точка минимума. Значения в экстремумах равны:
f (1/3)= (1/3)3-2 (1/3)2+ 1/3= 4/27; f (1)= 1-2 +1=0
6. Составим таблицу по результатам исследования
| х | (-∞, 1/3) | 1/3 | (1/3, 1) | 1 | (1,+ ∞) |
| f'(x) |
+
|
0 |
- |
0 |
+ |
| f(х) | ↑ |
4/27 |
|
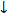
0 |
↓
|
7. Найдем абсциссы точек пересечения графика с осью Ох:
х3 -2х2 + х = 0,
х (х2 -2х + 1) =0,
х (х -1)2 =0,
х = 0 или х = 1.
8. Построим график функции
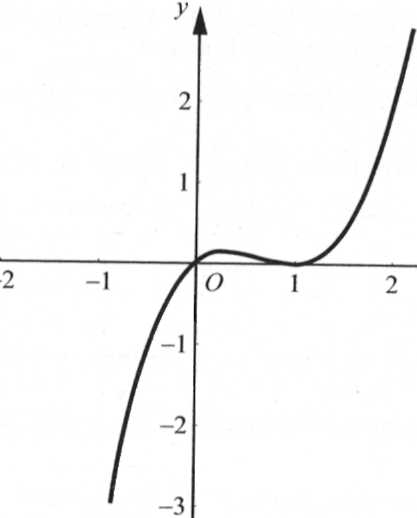
Задание 2. Постройте график функции f(х) = 1- 5/2 х2 -х5.
Решение:
1. Область определения D(f) =R.
2. Найдем производную f'(x) = -5х - 5х4 = -5 х (1 +х3).
3. Найдем критические точки, решив уравнение f /(x) = 0.
-5х(1 + х3) = 0
х1 =0, х2 = -1.
4. Найдем промежутки возрастания и убывания, используя метод интервалов и правило чередования знаков для производной f'(x) =-5х (1+х3) имеем 3 интервала знак постоянства: (-∞;-1); (-1;0); (0;+ ∞).
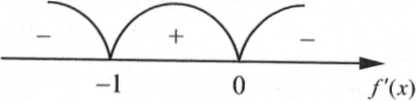
f /(x)0 на промежутке (-1; 0), значит, функция возрастает на этом промежутке;
f /(x) 0 на промежутках (-∞;—1) и (0; +∞), значит, функция на них убывает.
5. При переходе через точку х = -1 производная меняет знак с «-» на «+», значит, это точка минимума. При переходе через точку х = 0 производная меняет знак с «+» на «-», значит, это точка максимума. Значения в экстремумах равны: f(-1)=-0,5 f(0)=1
6.Составим таблицу
| х | (-∞, -1) | -1 | (-1, 0) | 0 | (0,+ ∞) |
| f'(x) |
-
|
0 |
+ |
0 |
- |
| f(х) | ↓ |
-0,5 |
↑ |
1 |
↓
|
7. Построим график
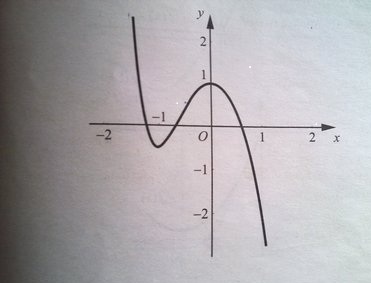
Схема нахождения наибольшего и наименьшего значений функции f(x), непрерывной на отрезке [a; b].
Найти значения функции в концах отрезка, т.е. f(a) и f(b);
Найти значения функции в тех критических точках, которые принадлежат интервалу (a ,b);
Из найденных значений выбрать наибольшее и наименьшее.
Образец решения
Пример: Найти наименьшее и наибольшее значение функции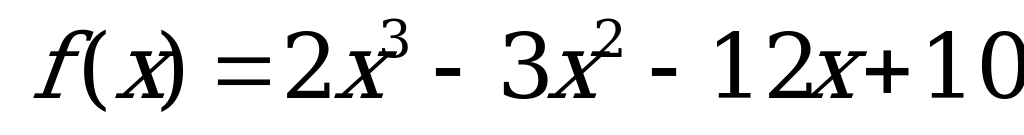 
на отрезке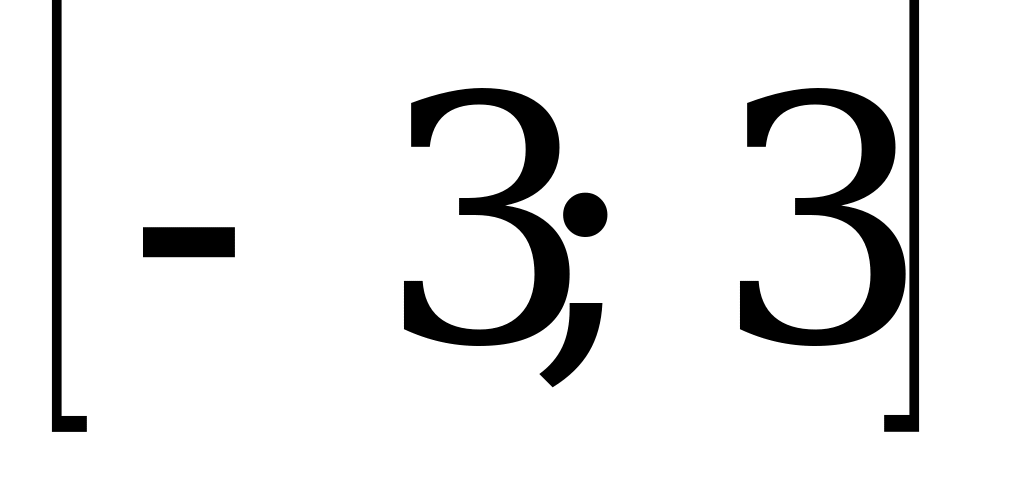 
Решение: Функция 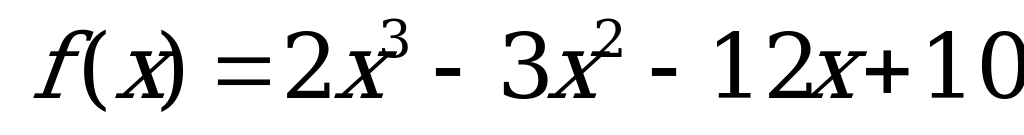непрерывна на отрезке .
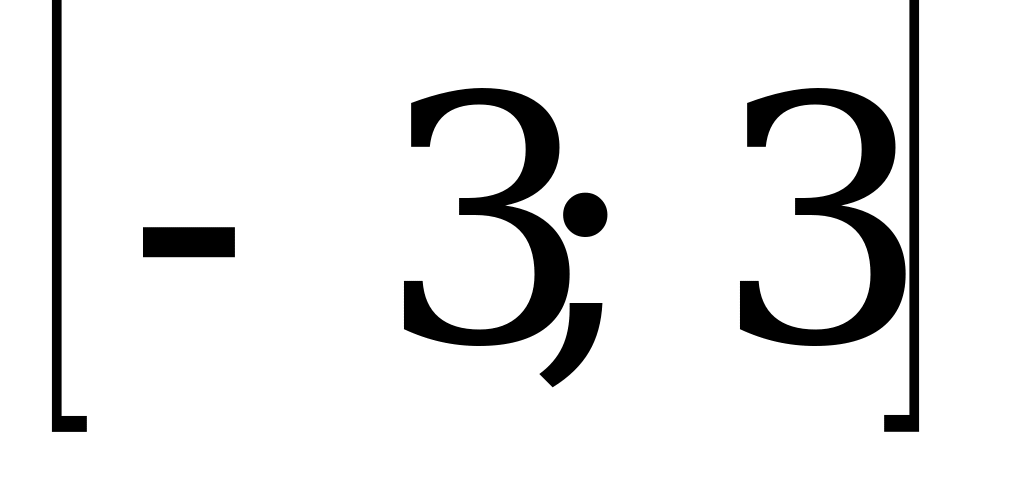1. Найдём значения функции на концах отрезка: f(-3)=-35, f(3)=1;
2. Найдем критические точки функции, для этого вычислим ее производную и приравняем ее нулю: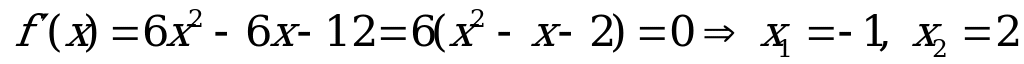
- критические точки функции, причем обе они принадлежат отрезку 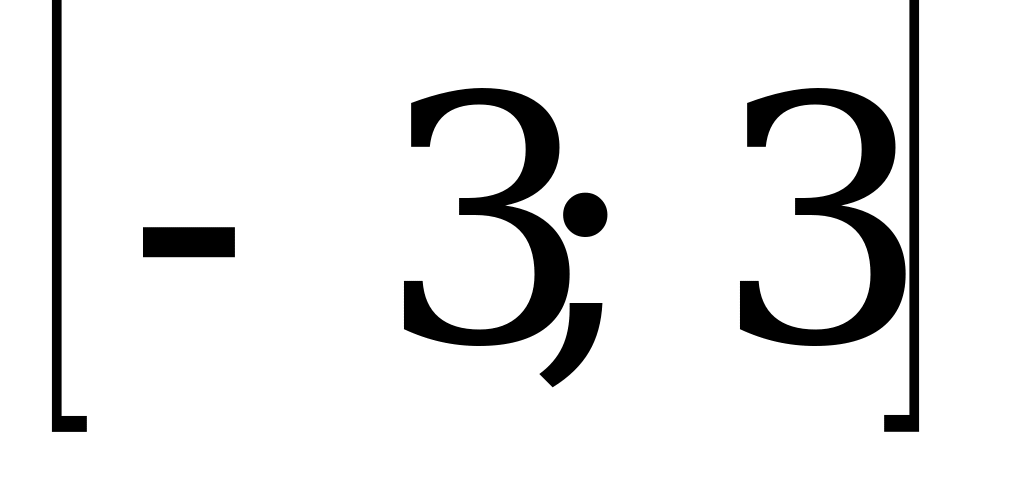. Вычислим значения функции в критических точках: f(-1)=17, f(2)=-10;
3. Т.о., наименьшее значение функции равно -35 и достигается на левой границе отрезка, а наибольшее значение функции равно 17 и достигается во внутренней точке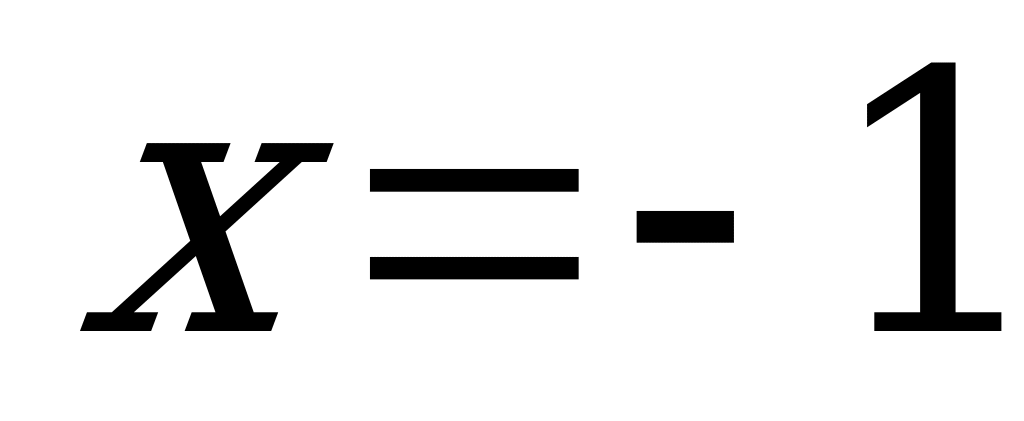 
.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
