Лекция 2. Операции над графами
Рассмотрим семь операций над графами, три из которых являются бинарными, включающими два графа, а остальные четыре – унарные, т. е. определены на одном графе.
Объединение графов G1 и G2 , обозначаемое как 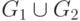 , представляет такой граф
, представляет такой граф 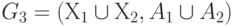 , что множество его вершин является объединением Х1 и Х2 , а множество ребер – объединением A1 и A2 . Граф G3 , полученный операцией объединения графов G1 и G2 , показан на рис. 2.1,д, а его матрица смежности – на рис. 2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2 .
, что множество его вершин является объединением Х1 и Х2 , а множество ребер – объединением A1 и A2 . Граф G3 , полученный операцией объединения графов G1 и G2 , показан на рис. 2.1,д, а его матрица смежности – на рис. 2.1,е. Матрица смежности результирующего графа получается операцией поэлементного логического сложения матриц смежности исходных графов G1 и G2 .
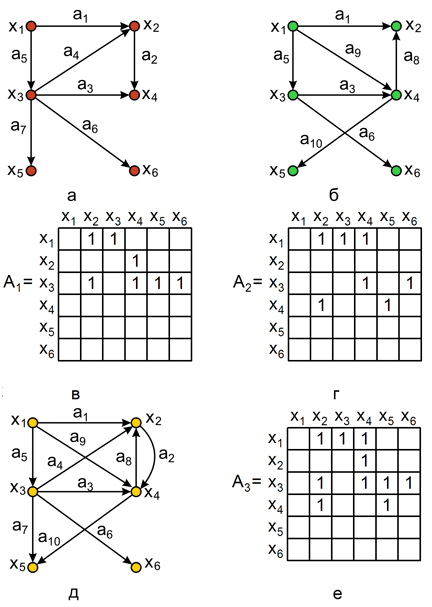
Рис. 2.1.
Пересечение графов G1 и G2 , обозначаемое как  , представляет собой граф
, представляет собой граф  . Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2 . Операция пересечения графов
. Таким образом, множество вершин графа G4 состоит из вершин, присутствующих одновременно в G1 и G2 . Операция пересечения графов  показана на рис. 2.2,в, а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.г.
показана на рис. 2.2,в, а результирующая матрица смежности получается операцией поэлементного логического умножения матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.г.
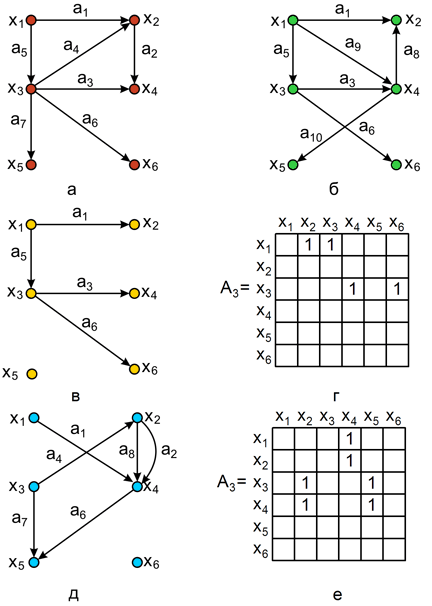
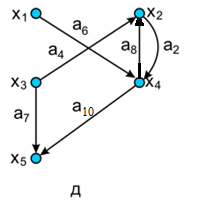

Рис.2.2. Операция пересечения и кольцевой суммы: а – граф G1 ; б – граф G2 ; в – граф  ; г – матрица смежности графа
; г – матрица смежности графа  ; д – граф
; д – граф  ; е – матрица смежности графа
; е – матрица смежности графа 
Кольцевая сумма двух графов G1 и G2 , обозначаемая как  , представляет собой граф G5 , порожденный на множестве ребер
, представляет собой граф G5 , порожденный на множестве ребер  . Другими словами, граф G5 не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G1 , либо в G2 , но не в обоих одновременно. Кольцевая сумма графов G1 и G2 показана на рис. 2.2,д, а результирующая матрица смежности получается операцией поэлементного логического сложения по mod 2 матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.е.
. Другими словами, граф G5 не имеет изолированных вершин и состоит только из ребер, присутствующих либо в G1 , либо в G2 , но не в обоих одновременно. Кольцевая сумма графов G1 и G2 показана на рис. 2.2,д, а результирующая матрица смежности получается операцией поэлементного логического сложения по mod 2 матриц смежности исходных графов G1 и G2 . показана на рис. 2.2.е.
Легко убедиться в том, что три рассмотренные операции коммутативны т. е. 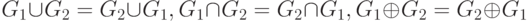 , и многоместны, т. е.
, и многоместны, т. е. 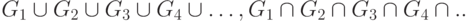 . и так далее.
. и так далее.
Рассмотрим унарные операции на графе.
Удаление вершины. Если хi -вершина графа G = (X, A), то G–хi -порожденный подграф графа G на множестве вершин X–хi , т. е. G–хi является графом, получившимся после удаления из графа G вершины хiи всех ребер, инцидентных этой вершине. Удаление вершины х3 показано на рис. 2.3,б (для исходного графа, изображенного на рис. 2.3,а). Матрица смежности исходного графа представлена на таблице 2.1а). Результирующая матрица смежности графа после выполнения операции удаления вершины хi получается путем удаления соответствующего i - го столбца и i -ой строки из исходной матрицы и "сжимания" матрицы по вертикали и горизонтали начиная с (i+1) - го столбца и (i+1) -ой строки ( таблица 2.1б). В дальнейшем элементы графа могут быть переобозначены.
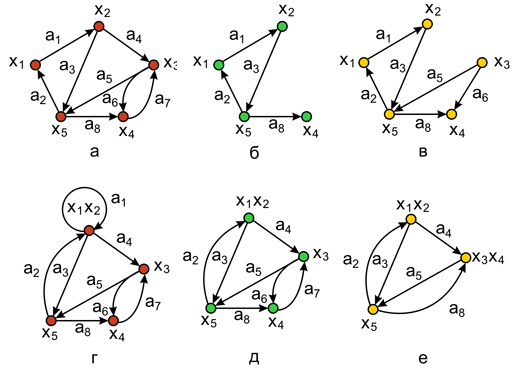
Рис. 2.3.
Удаление ребра или удаление дуги. Если ai - дуга графа G = (X, A), то G-ai – подграф графа G, получающийся после удаления из G дуги ai . Заметим, что концевые вершины дуги ai не удаляются. Удаление изграфа множества вершин или дуг определяется как последовательное удаление определенных вершин или дуг. Удаление дуг a4 и a7 показано на рис. 2.3,в. Результирующая матрица смежности графа после выполнения операции удаления дуги ai получается путем удаления соответствующих элементов из исходной матрицы ( таблица 2.1в).
| Таблица 2.1a. | |
| X1 | X2 | X3 | X4 | X5 | | X1 |
| 1 |
|
|
| | X2 |
|
| 1 |
| 1 | | X3 |
|
|
| 1 | 1 | | X4 |
|
| 1 |
|
| | X5 | 1 |
|
| 1 |
|
| | Таблица 2.1б. | |
| X1 | X2 | X4 | X5 | | X1 |
| 1 |
|
| | X2 |
|
|
| 1 | | X4 |
|
|
|
| | X5 | 1 |
| 1 |
|
| | Таблица 2.1в. | |
| X1 | X2 | X3 | X4 | X5 | | X1 |
| 1 |
|
|
| | X2 |
|
|
|
| 1 | | X3 |
|
|
| 1 | 1 | | X4 |
|
|
|
|
| | X5 | 1 |
|
| 1 |
|
|
| Таблица 2.1г. | |
| X1-2 | X3 | X4 | X5 | | X1-2 | 1 | 1 |
| 1 | | X3 |
|
| 1 | 1 | | X4 |
| 1 |
|
| | X5 | 1 |
| 1 |
|
| | Таблица 2.1д. | |
| X1-2 | X3 | X4 | X5 | | X1-2 |
| 1 |
| 1 | | X3 |
|
| 1 | 1 | | X4 |
| 1 |
|
| | X5 | 1 |
| 1 |
|
| | Таблица 2.1е. | |
| X1-2 | X3-4 | X5 | | X1-2 |
| 1 | 1 | | X3 |
|
| 1 | | X5 | 1 | 1 |
|
|
Замыкание или отождествление. Говорят, что пара вершин хi и xj в графе G замыкается (или отождествляется), если они заменяются такой новой вершиной, что все дуги в графе G, инцидентные хi и xj , становятся инцидентными новой вершине. Например, результат замыкания вершины х1 и х2 показан на рис. 2.3,г для графа G ( рис. 2.3,а). Матрица смежности графа после выполнения операции замыкания вершин хi иxj получается путем поэлементного логического сложения i - го и j - го столбцов и i -ой и j - строк в исходной матрице и "сжимания" матрицы по вертикали и горизонтали ( таблица 2.1г).
Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. Граф, изображенный на рис. 2.3,д получен стягиванием дуги a1 , а на рис. 2.3,е – стягиванием дуг a1, a6 и a7 . Соответствующие результирующие матрицы смежности показаны в таблицах 2.1д и 2.1е.































