Занятие 29. Тема «Операции над графами»
План лекции:
-
Полный граф
-
Бинарные операции над графами
-
Унарные операции над графами
Полный граф
Полным графом G называется граф с п вершинами без петель, кратных и противоположных дуг (ориентация безразлична), у которого любые две вершины соединены ребром. Например 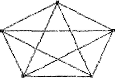
Бинарные операции над графами
Бинарные операции включают два графа.
Бинарные операции над графами. Наиболее важными бинарными операциями являются: объединение, пересечение, кольцевая сумма и дополнение. Операции могут выполняться как графически, так и с помощью матриц смежности каждого графа. Рассмотрим все бинарные операции двумя способами.
-
Объединение. Граф G=(X,А) называется объединением (или наложением) графов G1= (Х1, А1) и G2 = (Х2, А2), если множество его вершин является объединением Х1 и Х2, а множество ребер - объединением А1 и А2: Другими словами, в один граф добавляются все вершины и ребра одного и второго графа (одинаковые остаются по одному).
G = G1 G2 = (X1
G2 = (X1  X2, А1
X2, А1 А2).
А2).




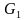

В матрице смежности объединенного графа работает операция дизъюнкция по таблице истинности. Матрицы смежности графов G1 и G2 имеют вид

А1= А2=
Объединение графов G1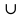 G2 выглядит так
G2 выглядит так 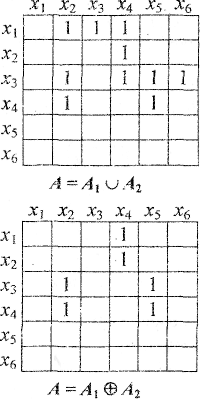
-
Пересечение. Граф G=(X,А) называется пересечением графов G1=(Х1,А1) и G2=(Х2,А2), если множество его вершин является пересечением Х1 и Х2, а множество ребер - пересечением А1 и A2: G = G1  G2 =(X1
G2 =(X1  X2, A1
X2, A1  А2). Другими словами, в один граф добавляются только те вершины и ребра, которые одинаковые и у одного и у второго графа.
А2). Другими словами, в один граф добавляются только те вершины и ребра, которые одинаковые и у одного и у второго графа.




G
G1

G2
-
-
Матрица смежности пересеченного графа G1  G2 составляется по конъюнкции и выглядит так
G2 составляется по конъюнкции и выглядит так
3. Кольцевая сумма. Граф G=(X,А)=G1 G2, порожденный на множестве ребер A1
G2, порожденный на множестве ребер A1 A2, представляет собой кольцевую сумму двух графов G1=(Х1,А1) и G2 =(Х2, А2). Другими словами, в кольцевой граф добавляются те ребра, которые разные у обоих графов, а одинаковые убираются (вершины остаются все). Кольцевая сумма графов G1 и G2 показана на рисунке:
A2, представляет собой кольцевую сумму двух графов G1=(Х1,А1) и G2 =(Х2, А2). Другими словами, в кольцевой граф добавляются те ребра, которые разные у обоих графов, а одинаковые убираются (вершины остаются все). Кольцевая сумма графов G1 и G2 показана на рисунке:



G2

Матрица смежности кольцевого графа G1 G2 составляется по сложению по модулю два и выглядит так
G2 составляется по сложению по модулю два и выглядит так 
4. Разность. Граф G=(X,А) называется разностью графов G1=(Х1,А1) и G2=(Х2,А2), если множество его вершин является разностью Х1 и Х2, а множество ребер - разностью А1 и. A2: G = G1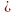 G2 = (X1
G2 = (X1 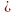 X2, А1
X2, А1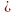 А2). Операция разности некоммутативна, то есть G1
А2). Операция разности некоммутативна, то есть G1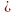 G2
G2  G2
G2  G1. Другими словами, в разностный граф добавляются только те ребра, которые есть у первого графа, но нет у второго (вершины остаются все).
G1. Другими словами, в разностный граф добавляются только те ребра, которые есть у первого графа, но нет у второго (вершины остаются все).

G



G1

G2
Матрица смежности разностного графа G1 G2 составляется по вычитанию (1-1=0, 1-0=1, 0-1=0, 0-0=0) и выглядит так
G2 составляется по вычитанию (1-1=0, 1-0=1, 0-1=0, 0-0=0) и выглядит так
5. Дополнением графа G=(X,А1) является граф  =(X,А2) , у которого множество вершин совпадает с множеством вершин графа G, а множество ребер, не принадлежит графу G, то есть в
=(X,А2) , у которого множество вершин совпадает с множеством вершин графа G, а множество ребер, не принадлежит графу G, то есть в  любые две вершины смежны, если только они не смежны в G. Другими словами, в дополненный граф добавляются только те ребра, которых не хватает до полного графа (вершины остаются все).
любые две вершины смежны, если только они не смежны в G. Другими словами, в дополненный граф добавляются только те ребра, которых не хватает до полного графа (вершины остаются все).
Матрица смежности полного графа, состоит из всех 1, кроме главной диагонали. Матрица смежности дополненного графа G1  G2 составляется инверсии и выглядит так
G2 составляется инверсии и выглядит так
G: 
Унарные операции над графами
Унарные операции определены на одном графе. Рассмотрим их.
-
Удаление вершины. Если xi - вершина графа G=(X,А), то G-i является графом, получившимся после удаления из графа G вершимы i и всех ребер, инцидентных этой вершине. Удаление из графа вершины влечет удаление всех ребер, входящих в эту вершину. Удаление вершины 2 показано на рисунке:
- исходный граф G - граф G-2
-
Удаление ребра или удаление дуги. Если аi - ребро графа G = (X, А), то G-аi является графом, получающимся после удаления из G ребра аi. Заметим, что концевые вершины ребра аi, не удаляются. После удаления всех ребер граф оказывается без ребер. Удаление ребер (5,4) и (1,2) показано на рисунке:
- исходный граф G - граф G-(5,4),(1,2)
-
Замыкание или отождествление. Говорят, что пара вершин хi и хj в графе G замыкается (или отождествляется), если они замыкаются такой новой вершиной, что все дуги в графе G, инцидентные хi и хj, становятся инцидентными новой вершине. После замыкания, дуга или ребро, находящееся между вершинами, станет петлей. Например, результат замыкания вершин 2 и 3 показан на рисунке:









2,3?
4
5
1
- исходный граф G
-
Стягивание. Под стягиванием подразумевают операцию удаления дуги или ребра и отождествление его концевых вершин. После стягивания, две вершины совмещаются в одну, а ребро или дуга, находящаяся между ними, удаляется. Граф, изображенный на следующем рисунке, получен стягиванием ребра (1,5):

2
- исходный граф G
Самостоятельная работа студентов
-
Переписать лекцию в тетрадь и прислать фото
-
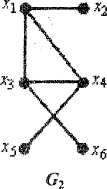
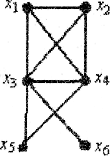
Выполнить все бинарные операции (кроме дополнения) двумя способами для следующих графов:
G1: G2:
-
Выполнить все унарные операции для следующего графа по следующим параметрам (удаление вершины 3, удаление дуги (46), замыкание вершин 1 и 3, стягивание дуги (46)).
Выполненные задания отправить на адрес электронной почты преподавателя в виде фото, сделанное из тетради.








 G2 = (X1
G2 = (X1 



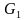
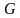





 G2 =(X1
G2 =(X1 





















